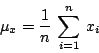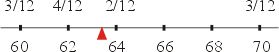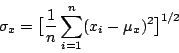现代统计学的发展 第一部分
转自:
http://episte.math.ntu.edu.tw/articles/mm/mm_03_3_09/index.html
两岸数学词汇存有差异, 请参照[遇见数学]之前整理发布的《两岸数学词汇对照表》
「统计」这个名词的意义因人而异,对一般人而言,统计是任何方面专家们用以支持其论点的一大堆数字;对于略具常识的人来讲,这个名词代表用以摘要和解释一堆数据如计算平均数(mean) 与标准差(Standard deviation) 的程序之类的概念。但是对于从事统计工作的人员而言,统计是依小量数据(样本)所提供的资料以估计预测某研究对象如群体的方法。或者更广义地说,统计为面对不定状况制定决策提供方法的科学。
虽然统计的起源可追溯至十八世纪甚至更早,然而统计学主要的发展却迟至十九世纪末叶二十世纪初期才真正开始。到了四十年代才逐渐成熟,统计学和机率论的关系异常密切,事实上任何统计问题的研究都必须牵涉到机率论的运用,因为后者实为前者的主要工具。
统计人员对如下所举之类问题的答案深感兴趣:是否接受本批送验成品?吸烟与得癌症有关吗?张三会于下届选举中获胜吗?为了回答上述问题,我们必须由具「代表性」的特殊状况以「了解」一般的状况,由样本「推测」群体。因此,由统计人员所推测得到的结论都不是绝对肯定可以接受。事实上,统计人员的职责之一是量度他所得结论肯定的程度,但是我们不能以为统计的缺乏肯定性而误认为统计数学不严密,因为构成统计基础的数学是机率论,它有固若磐石的数理化基础和经严密证明的定理。
一般而言,我们可以把统计问题分成两类: 叙述统计和推论统计,简单的说:任何对数据(即样本)的处理导致预测或推论群体的统计称为推论统计。反之,如果我们的兴趣只限于手头现有的数据,而不准备把结果用来推论群体则称为叙述统计。举个例子来说,依据过去十年来的统计,每年来华观光的人数,平均每人在台停留的日数,平均每人每天在华的花费,十年内那一年创最高记录等等都是属于叙述统计的范围;但是如果我们根据这些年所得的数据来预测来年可能的观光客人数就是推论统计的问题了。十年前的初级统计课本大多谈叙述统计,如今由于计算机的盛行,这部份的工作大多利用计算机来解决,称为数据处理,而一般统计书的重点别放在推论统计。
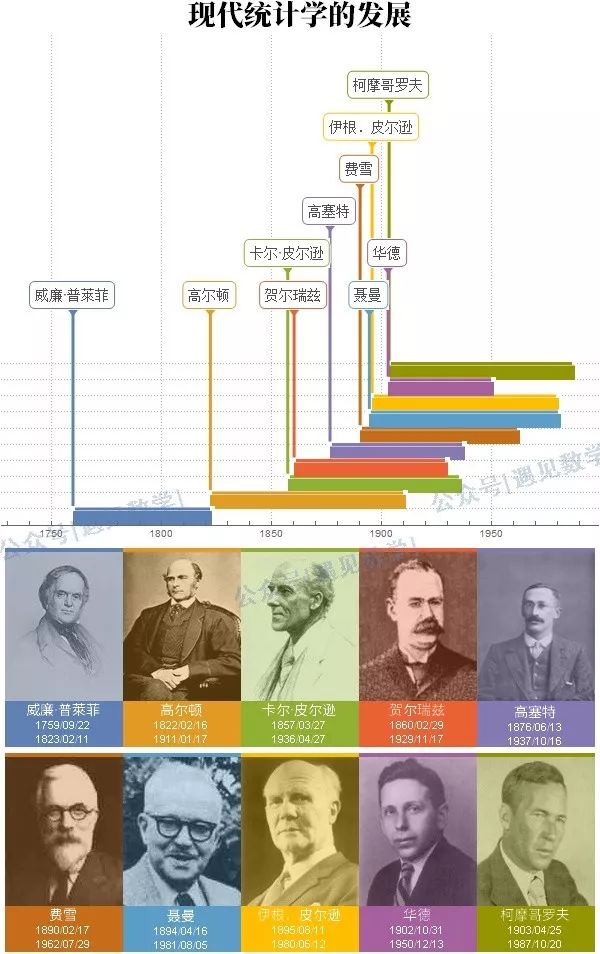
大致说来,推论统计分为三大类,就是估计,检定和分类与选择。譬如说,张三想竞选台北市议员,他想估计一下可能有多少人会投票给他,于是他以随机抽样的方式,询问100位有投票权的市民的意见,而后根据所得结果推论可能全市有多少人会选他,这是估计问题。又如某家庭主妇想知道她心中怀疑洁王牌洗衣粉的洗净力是否比爱王牌洗衣粉强,首先假设洁王牌比爱王牌好,然后经过试验来测定这假说是否成立,在本例中,我们并不想估计任何参数,而只是想检验事先所叙述的假设是否成立其可靠性有多大,这就是检定问题。还有,新制造的三种药品中那几种比目前所用的这种药品有效呢?这是选择的问题。如果我们把统计设想为经由抽样以制定决策的科学,那么我们似乎宜以十九世纪末期高尔顿爵士(Sir Francis Galton, 1822~1911)和卡尔·皮尔逊(Karl Pearson, 1857~1936)的论述做为它的起点。从那时开始,现代统计理论的发展可略分为四大思潮,在这四大时期,每一阶段都是以一位伟大的统计学家的专著为先导[注1] 。
第一阶段随着1899年高尔顿的《Nature Inheritance》一书的出版而展开序幕,该书除了其本身的价值外,还引发了杰出的统计学家卡尔.皮尔逊对统计学的兴趣。在此之前,皮氏只是在伦敦大学的大学部(University College) 执教的数学教员。当时,这「所有知识都基于统计基础」的想法引起了他的注意。
1890年他转到格里辛学院(Gresham College),在那里他可讲授任何他希望讲授的课程,皮氏选了一个题目「现代科学的范围与概念」(the Scope and Concepts of modern Science) 在他的授课中他越来越强调科学定律的统计基础,后来他全神集中致力于统计理论的研究。不久他的实验室成为世界各地人们学习统计和回国点燃「统计之火」的研究中心。经由他热心的提倡,科学工作者逐渐由对统计研究不感兴趣的境地转而成为热切地努力发展新理论和搜集并研究得自各方面的数据。人们越来越深信统计数据的分析能为许多重要的问题提供解答。
海伦·华克(Helen Walker)描述皮氏小时候的一则轶事,生动地显示他往后事业中所表现的特色[注2] 。有人问皮尔逊他所记得最早的事,他说「我不记得那时是几岁,但是我记得是坐在高椅子上吸吮着大拇指,有人告诉我最好停止吮它,不然被吮的大拇指会变小。我把两手的大拇指并排看了很久,它们似乎是一样的,我对自己说:我看不出被吸吮的大拇指比另一个小,我怀疑她是否在骗我」。
在这个单纯的故事中,海伦华克指出「不盲信权威,要求实证,对于自己对观测数据的意义的解绎深具信心,和怀疑与他的判断不同的人态度是否公平」这些就是皮氏一生独具的特征。
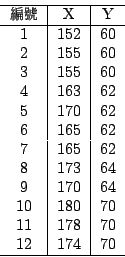
表一
这个第一阶段的特点就是人们对统计的态度转变了,统计的重要性被科学界所承认。除此之外,在统计技巧上也有很多的进展,我们利用上面这个十二个人的身高和体重的数值表介绍一些最基本的统计观念,其中身高 X 以公分为单位,体重 Y 以公斤为单位。
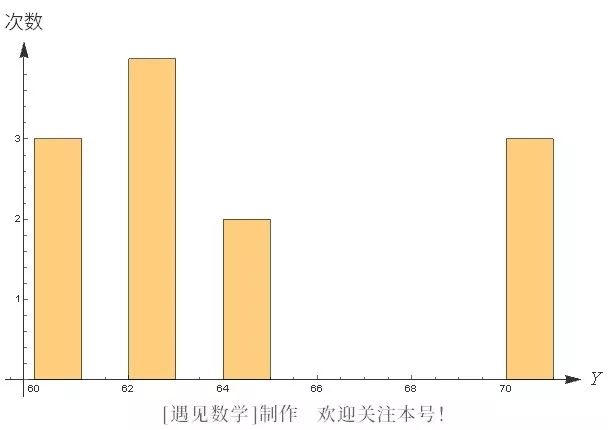
为了对这组资料得到一点概念,我们把它列成图形。英人普莱菲(William Playfair, 1759~1823)被公认为将图形表示的概念介绍到统计学的第一人。他的著作,大多为关于经济学,多采用图形如直方图、条形图。在我们上述问题中,用次数图就能很清楚地表示出来,图一就是身高 X 的次数图,体重 Y 的次数图也很容易表示。有兴趣的读者不妨一试。虽然这类图形能帮助我们的直觉,但是如果想对这些数据更一步了解,我们必得进一步用某些量来描述它们。在这类数量中最重要之一是对于集中趋势的测度。最早的集中趋势的测度实际上可追溯至古希腊,是算术平均数,即
其中 x i 代表变数 X 的数值,n 为观测值的总个数,计算结果得到身高的平均数 为166.66,体重的平均数
为63.83,为了理解这个观念的特性,我们把它的定义改写成
其中 f j 是 x j 出现的次数,并对不同的 X 变数 x j 值求和。
假设有一根无重的木杆,其上刻着变数Y的各不同值的刻度,并且设想在 x j 处挂着质量 的物品,则整个体系的质量为 1,而
为质量重心,也就是说如果把支点设于
,则整个体系会趋于平衡,以本例的身高而言,其体系如图二所示。
图二 |
这种对平均数的解释在以后我们思考连续分配观念时,很有帮助。
虽然中位数 (median)观念可能早已有之,但是迟至1883年才经由高尔顿把它引入统计,成为集中趋势第二种测度[注3] 。所谓中位数就是所有观测值依大小排起来,中间的那个数,若是偶数个数就是两个中间数的平均数,在我们例子中身高的中位数为165。
另外还有一个集中趋势的测度是众数,1894年左右由卡尔.皮尔逊所介绍。众数如果存在的话,就是出现次数最频繁的数值,如果两个或两个以上的数值出现次数相同,众数就不太有意义了,在我们例子中体重的众数是62。
如果变数 X 的分配是完全对称,即其次数图完全地对称于一垂直线,那么平均数、中位数和众数(如有一众数存在的话)会重合为一点。读者们应注意,反过来说并不成立。也就是说不对称的图形也可有平均数,中位数和众数重合的情形(即平均数、中位数和众数重合并不保证图形为对称)。
对大多数的目的而言算术平均数是最常用的集中趋势测度,这当然有它学理上的意义。虽然有时候计算相当费时,中位数也有它的优点,它不受少数极端值的影响。例如在我们的例题中,若把一个身高180公分的人换成一个200公分的人,平均数就会受到很大的影响,而中位数却全然不变。
其次我们谈一下「离差」(dispersion) 的测度,它是数据以平均数为准对于分散程度的测度。最早这种测度大概是贝塞(Bessel)于1815年用于有关天文学问题的「可能误差」。目前最通用的是「标准差」σ,这个名词是1894年卡尔.皮尔逊所创。
离散变数 X 的标准差定义为
由这个公式可以看出若数据非常分散,值会很大,但当数据集中于平均值附近时则
会小。
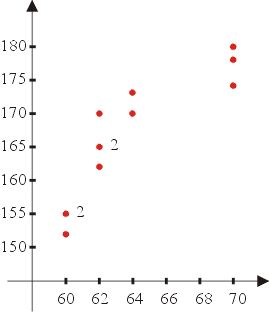
为了介绍相关的观念,我们回头再仔细看一下表一中的身高和体重,数值显示这两个变数似乎有某种相关存在,根据常识,高的人通常要比矮的人重,在这些数据点绘在直角坐标的平面上,可以看出它们之间的关系,称为分布图(参见图三)
图三 |
如果它们之间为线性关系,则点的趋向会呈现在直线的附近。(未完待续)