【NeurIPS'21】使用典型相关分析轻松高效地实现大图上的自监督表示学习

2022 年 1 月 3 日 图与推荐

论文标题: From Canonical Correlation Analysis to Self-supervised Graph Neural Networks

论文链接: https://proceedings.neurips.cc/paper/2021/hash/00ac8ed3b4327bdd4ebbebcb2ba10a00-Abstract.html

代码链接: https://github.com/hengruizhang98/CCA-SSG

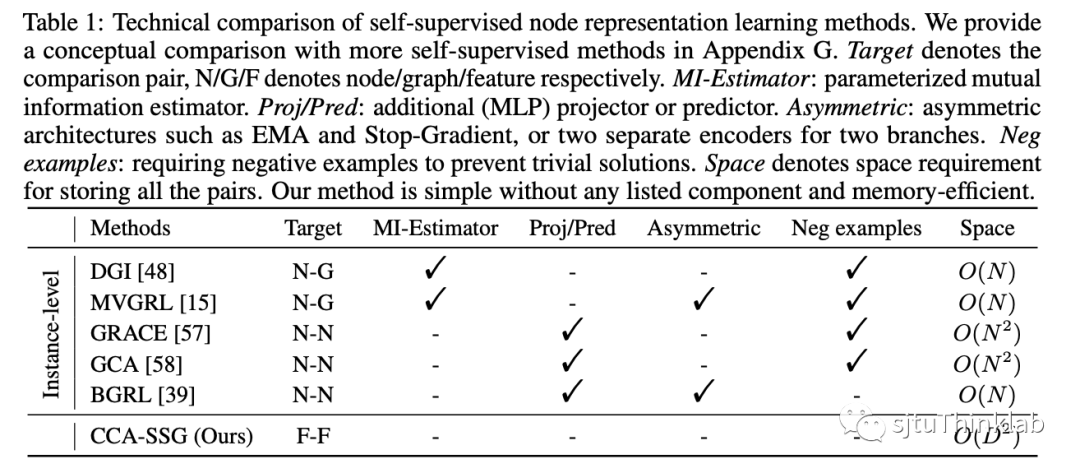
本文提出了一种简单且有效的图上的自监督表示学习方法。与流行的对比学习(contrastive learning)的方法类似，我们首先使用图上的data augmentation来生成输入图的两个视图(views). 然而,和基于样本区分(instance-level discrimination)思想的对比学习不同，我们基于典型相关分析(Canonical Correlation Analysis, CCA)的思想来优化两个view的embedding的相关程度(feature-level regularization). 我们的理论分析表明我们的方法可以被视为信息瓶颈准则(Information Bottleneck Principe)在多视图自监督表示学习(multi-view self-supervised learning)场景下的具体实现. 我们在7个节点分类数据集上的实验表明, 我们的方法能以更快的训练时间，更低的计算开销得到更为优越的性能. 下表是我们的方法与目前主流方法的一个简单对比，其中我们的方法不需要各种多余的设计以及组件，并且有着线性的时空复杂度.

背景知识

从互信息与样本区分的角度理解对比学习

对比学习(contrastive learning),或多视图对比学习(multi-view contrastive learning)是目前最流行的自监督学习方法: 给定multi-view的输入数据(通常是由data augmentation生成), 以及由encoder得到的它们的低维向量表示, 对比学习希望最大化正样本对的相似度 , 而最小化负样本对的相似度 . 对比学习的成功常常被归因于对比损失函数与互信息的联系: 如果将和视为两个view的embedding的随机变量，而视为其样本，则对比学习的目标是最大化和的互信息 [1]. 例如, 常用的对比损失函数, Deep Infomax loss[2] 和 InfoNCE loss[3]都可以被视为估算了两个随机变量的互信息的下界. Deep Infomax loss的优点在于每一对正样本只需一个负样本，因此它的计算复杂度是 , 其中是batch size, 是embedding dimension，然而它对互信息估算的方差比较大，因而学到的embedding的质量比较一般. 相比之下，InfoNCE loss的每一对正样本需要大量的负样本对 (如将整个batch的其他样本都作为负样本)来降低互信息估计的误差，因此它的计算复杂度是 .

图上的自监督节点表示学习

基于对比学习的自监督学习模型在CV领域已经取得了极大的成功，类似的方法也被迁移到图上的表示学习任务上. 例如, Deep Graph Infomax (DGI)[4] 将节点embedding和整图的embedding作为正样本对，而把节点embedding和拓扑结构被破坏的图的embedding作为负样本对，然后使用参数化的Infomax loss function 进行优化. MVGRL[5]是DGI的进一步改进, 它使用graph diffusion来生成同一个图的两个view, 而正负样本对的选取则在两个view间交叉进行. 与DGI相比, MVGRL可以学到更优异的节点表示, 但是graph diffusion的计算开销十分巨大, 该模型只能通过子图采样在千级节点的子图上完成训练. GRACE[6]和GCA[7]使用了SimCLR[8]的框架: 首先使用data augmentation生成同一张图的两个view, 节点的embedding通过一个共享的GCN encoder得到, 最后使用InfoNCE loss进行优化. 然而受限于InfoNCE loss 的空间复杂度, GRACE和GCA都难以被直接应用在超过数万节点的大图上.

典型相关分析

典型相关分析[9](Canonical Correlation Analysis, CCA)是一种非常经典的多元分析方法，给定两个随机变量和，原始的CCA的目标是找到两个映射向量和，使得映射后的随机变量的相关系数最大, 这一目标可以被表示为如下的约束优化任务:

在维情况下，CCA希望找到k组映射向量，使得每组映射后的随机变量的相关程度最大，并且不同组映射后的随机变量尽可能的无关. 因此，后来的研究[10,11]开始使用深度学习来将CCA应用在mulit-view data中. 例如，假设是输入数据的两个view，那么我们希望优化以下目标

其中和是两个神经网络, 是单位矩阵.

CCA从特征相关(最大化相同维度的相关系数)与去相关（不同的维度的相关系数要为0）的角度提出了multi-view data的embedding应当具有什么样的性质. 考虑到在自监督学习中，我们通过data augmentation生成了特殊的multi-view data, 因此，我们考虑使用CCA作为自监督学习目标.

我们的方法

我们所提出的框架由三个简单的部分组成:

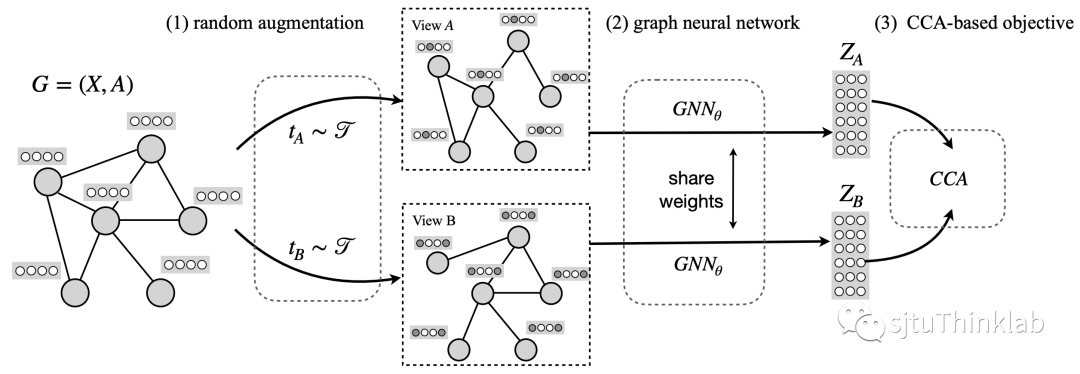
图上的随机增强(random augmentation): 这里我们采用GRACE所提出的两种方法: 1) random edge dropping ( 表示edge dropping的概率). 2）random feature masking( 表示edge dropping的概率.
图神经网络encoder: 1个单层或双层的GCN，用来得到node embedding.
基于CCA的目标函数

给定模型的超参数和 , 我们可以得到data augmentation的分布 . 在训练的每一步，我们首先从中随机采样出两个变换和 , 基于它们生成图的两个view: 和 . 紧接着我们使用一个共享的GCN encoder分别得到每个图的节点表示 , , 其中 , 表示embedding的维度.

我们进一步沿着样本方向对得到的node embedding进行标准化，使得每一维的均值为 , 而方差为 :

这样做的目的是让embedding的相关系数矩阵的对角元素均为1，以方便之后的计算.

接下来介绍目标函数，也是我们模型的关键. 我们提出优化如下的基于CCA的目标函数:

目标函数有两项: 1) 第一项我们称为invariance loss，它要求两个view的同一维度的相关系数要尽可能地大(两个view得到的embedding尽可能相似). 2) 第二项称为decorrelation loss, 它要求每一个view的embedding的不同维度所蕴含的信息尽可能的不相关(相关系数为 ). 则是一个超参数，负责均衡这两项的大小.

当训练结束后，我们固定GCN encoder的参数，使用原图作为输入即可得到学到的node embedding.

与其他自监督模型的对比

在这里我们将我们的模型与其他的自监督模型进行对比：之前的方法大多是基于对比学习，进行instance-level上的discrimination，希望将正样本对从数据样本对中区分出来，而我们的方法创新性地从embedding的相关与去相关出发，利用CCA去做feature-level的regularization. 与之前的方法相比，我们的模型不需要参数化的互信息估计器，不需要额外的projector/predictor，不需要负样本以及非对称的结构设计即可自然地避免trivial solution. 最重要的是，它具有线性的时间/空间复杂度，使得我们的方法能够轻松地拓展到万、十万级别的大图上进行整图训练，而不需要采样或其他额外处理。

理论分析

首先介绍接下来会用到的符号: 我们用表示输入数据，用表示通过data augmentation生成的数据. 和则分别表示对应的embedding. 则表示下游的任务. 和分别表示熵和信息. 我们对提出的目标函数进行了充分的理论分析与解读, 结论如下:

1）从熵和互信息的角度解读我们的目标函数

用表示的分布，用表示给定了输入数据后的条件分布，当和均为高斯分布时，公式(4)的第一项可以最小化条件熵 , 而第二项可以最大化熵 .

2) 与信息瓶颈准则的联系

定义自监督的信息瓶颈如下:

其中 . 那么优化公式(4)实际上是在最大化自监督的信息瓶颈loss, 因此我们的方法可以被视为信息瓶颈准则在自监督学习上的具体的实现.

3) 对下游任务的影响

假设数据扩充技术(data augmentation)并不会影响输入数据包含的对下游任务有用的信息，我们证明了我们的方法可以使得学到的embedding: 1)尽可能地保留与下游任务有关的信息; 2)尽可能地去除掉与下游任务无关的信息. 这个结论进一步阐述了为何通过自监督学习学到的embedding能够在多样的下游任务上具有优异的性能.

具体的介绍、分析以及证明请参考原文.

实验结果

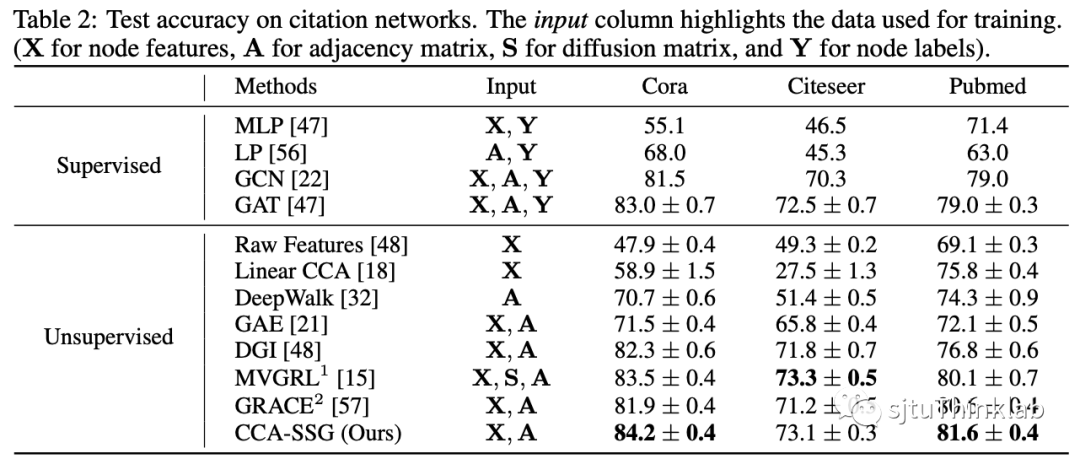
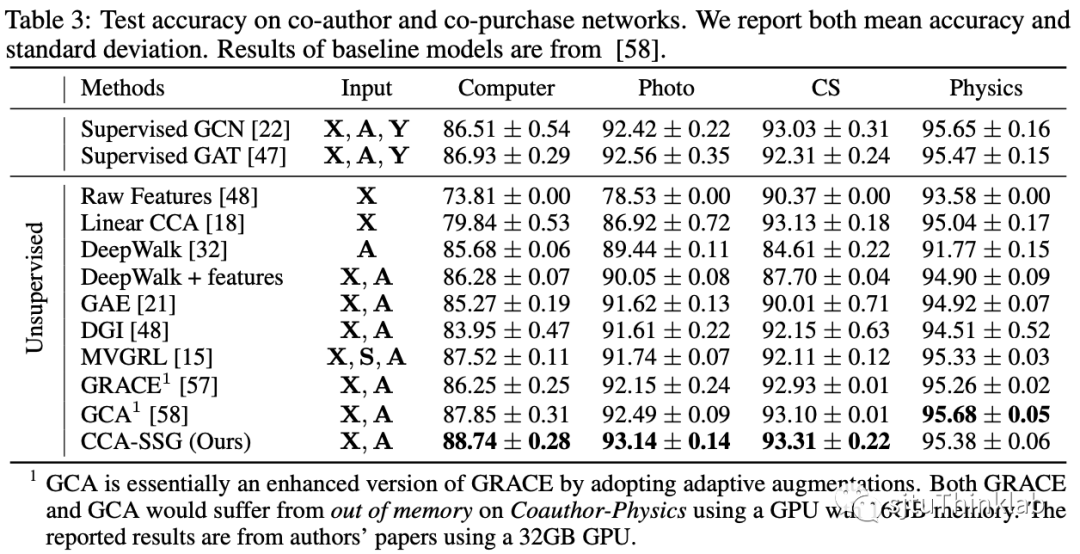
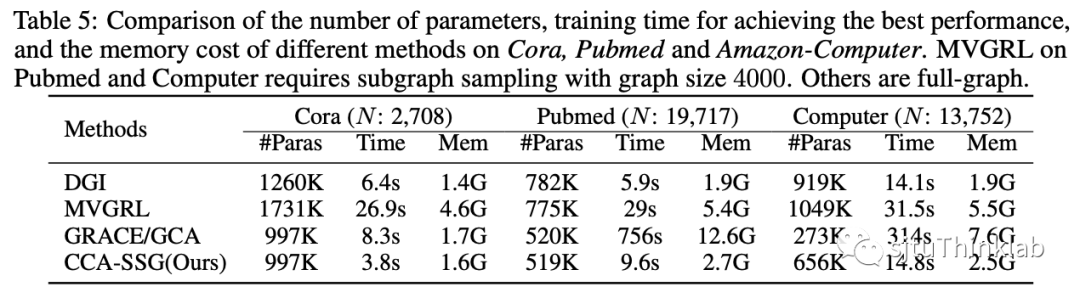
我们在经典的三个citation network: Cora, Citeseer, Pubmed，以及额外的4个社交网络基线数据集: Amazon-Computer, Amazon-Photo, Coauthor-CS, Coauthor-Physics进行了实验. 实验结果表明，我们的方法能够以更少的参数量，更快的训练速度，更低的内存占用得到相近、甚至更为优越的性能. 其他的消融研究以及参数分析请参考我们的论文.

如有疑问或希望进行进一步的讨论，请发邮件至hzhan55@uic.edu

参考文献

[1] Ben Poole, Sherjil Ozair, Aaron Van Den Oord, AlexAlemi, and George Tucker. On variational boundsof mutual information. In ICML, pages 5171–5180, 2019.

[2] R Devon Hjelm, Alex Fedorov, Samuel Lavoie-Marchildon, Karan Grewal, Adam Trischler, and Yoshua Bengio. Learning deep representations by mutual information estimation and maximization. In ICLR, 2019.

[3] Aäron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.

[4] Petar Velickovic, William Fedus, William L. Hamilton, Pietro Liò, Yoshua Bengio, and R. Devon Hjelm. Deep graph infomax. In ICLR, 2019.

[5] Kaveh Hassani and Amir Hosein Khas Ahmadi. Contrastive multi-view representation learning on graphs. In ICML, 2020.

[6] Yanqiao Zhu, Yichen Xu, Feng Yu, Qiang Liu, Shu Wu, and Liang Wang. Deep graph contrastive representation learning. arXiv preprint arXiv:2006.04131, 2020.

[7] Yanqiao Zhu, Yichen Xu, Feng Yu, Qiang Liu, Shu Wu, and Liang Wang. Graph contrastive learning with adaptive augmentation. In WWW, 2021.

[8] Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey E. Hinton. A simple framework for contrastive learning of visual representations. In ICML, Proceedings of Machine Learning Research, pages 1597–1607, 2020.

[9] Harold Hotelling. Relations between two sets of variates. Biometrika, 28:322–377, 1936.

[10] Galen Andrew, Raman Arora, Jeff A. Bilmes, and Karen Livescu. Deep canonical correlation analysis. In ICML, volume 28, pages 1247–1255, 2013.

[11] Xiaobin Chang, Tao Xiang, and Timothy M. Hospedales. Scalable and effective deep CCA via soft decorrelation. In CVPR, pages 1488–1497, 2018

登录查看更多