知乎热议：如何看待人教版教材用爱因斯坦相对论证明勾股定理？

---

  新智元报道  

来源：知乎

编辑：梦佳、雅新

【新智元导读】最近，人教版数学八年级下册自读课本中的一段内容出现了令人发指的错误上了热搜。用爱因斯坦相对论证明勾股定理可谓玄学。网友纷纷痛批误人子弟。

教材编错了！

 

最近人教版数学八年级下册自读课本中的一段内容引发了重大争议，简直误人子弟。

 

课本中写到爱因斯坦用相对论中的质能方程论证勾股定理，证明发表，震惊国际数学界，德国著名数学刊物「 Mathematische Annalen」 因此聘请爱因斯坦去做了多年主编。

       

勾股定理（Pythagoras theorem）是欧氏几何的基础定理，是几何学中的明珠，被誉为「几何学的基石」，在高等数学和其他科学领域也有着广泛的应用。勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。这样一条关键定理的证明，教材中出现谬误实属不应该。

课本中原文如下，

 

2005年是爱因斯坦建立相对论100周年，爱因斯坦在相对论中给出了一个著名的质能方程E=mc²，其中E表示物质所含的所有能量，m是物质的质量，c是光速。这个质能方程是现代制造核武器、核电站的理论基础。

 

据说，勾股定理也曾经引起了这位著名物理学家的浓厚兴趣，与大家不同的是，爱因斯坦是用相对论来证明勾股定理的。

 

假设直角三角形三条边为a，b，c，过直角顶点做斜边c的垂线段。

 

假设原三角形面积为E，根据相对论，有E=mc²

同理，内部分割出来的两个三角形的面积分别是

E(a)=ma²，E(b)=mb²，

因为内部两个三角形拼成原三角形，所以

E=E(a)+E(b)

也就是，

mc²=ma²+mb²，

两边约去m，就得到了勾股定理

c²=a²+b²

 

这当中的错误确实令人发指，相对论中E是能量，c是真空中的光速，和证明勾股定理中的E和c根本不挨着，最根本的表达式中各个字母的含义都弄错了，证明更是谈不上。

 

完全是通过作者的脑补，看到公式里的几个字母就和爱因斯坦的E=mc²联系到了一起。

那么爱因斯坦和勾股定理证明到底有没有关系呢？

爱因斯坦确实在1920到1928年担任了德国著名数学刊物「 Mathematische Annalen」 的主编之一，但是并不是因为「用相对论去证明勾股定理」。

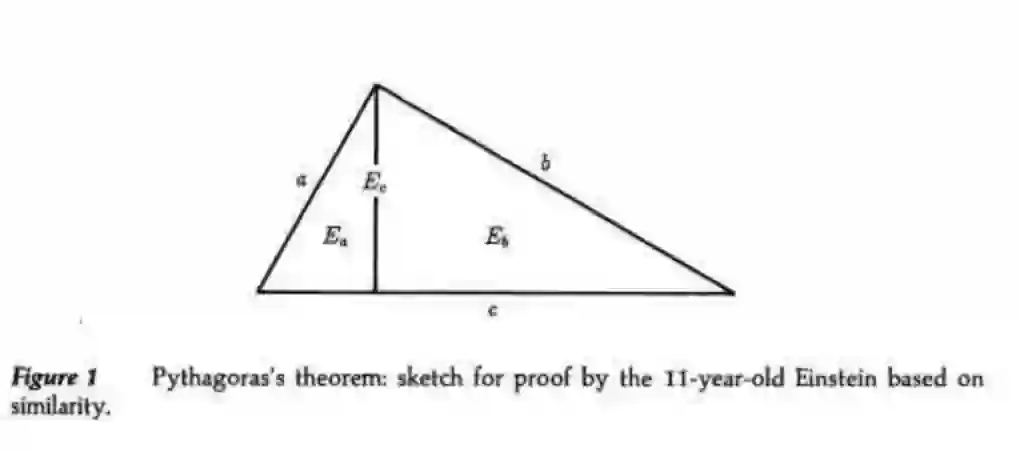
有网友翻出了英文资料的原文，书中写到爱因斯坦的叔叔在他11岁时证明勾股定理，小爱因斯坦觉得欧几里得的证明方法过于复杂。他想出了只需要在原本直角三角形的基础上增加一条线，就可以证明的方法。

如图三个直角三角形是互为相似三角形，用E表示面积，m表示正比系数，根据量纲分析，它们各自的面积正比于各自斜边边长的平方，就得出

 

Ea = ma²，Ec= mc²，Eb= mb²

 

因为Ea+Eb=Ec，所以ma²+mb²=mc²，由此得出a²+b²=c²

 

所以说无缘无故扯上了相对论质能方程确实不应该。

 

那么应该如何证明勾股定理呢？

 

证明勾股定理有很多种方法，我们举几个证明的例子

 

1 利用相似三角形性质证明

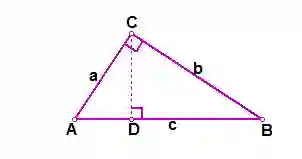
如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D

在ΔADC和ΔACB中，

∵ ∠ADC = ∠ACB = 90º，

∠CAD = ∠BAC，

∴ ΔADC ∽ ΔACB（相似三角形）

AD∶AC = AC ∶AB，

即 AC²=AD·AB

同理可证，ΔCDB ∽ ΔACB，从而有BC²=BD·AB .

∴AC²+BC²=(AD+DB)·AB=AB² ，即a²+b²=c².

 

2 勾股定理的证明方法3（赵爽证明）

 

赵爽是中国古代数学家，他用弦图证明了勾股定理

  

现代演绎为，

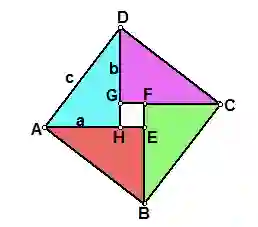
把这四个全等的直角三角形拼成如图所示形状。

∵ RtΔDAH ≌ RtΔABE

∴ ∠HDA = ∠EAB

∵ ∠HAD + ∠HDA = 90º

∴ ∠EAB + ∠HAD = 90º

∴ ABCD是一个边长为c的正方形，它的面积等于c²

∵ EF = FG = GH = HE = b-a ,

∠HEF = 90º

∴ EFGH是一个边长为b-a的正方形，它的面积等于（b-a)²

∴ 4x 1/2ab + (b-a)² =c²

∴ a²+b²=c²

中国古人果然有大智慧！

 

3 在欧几里得的《几何原本》一书中也给出勾股定理的证明。

 

证明的基本思路为：△ABC为一直角三角形，其中A为直角。从A点画一直线至对边，使其垂直于对边。延长此线把对边上的正方形一分为二。把上方的两个正方形，通过等高同底的三角形，以其面积关系，转换成下方两个同等面积的长方形，其长方形的面积分别与其余两个正方形相等。

其他证明方法还包括加菲尔德证法等等。

专家点评：把愚人节搞笑版勾股定理证明当真

来自新加坡国立大学的学者表示，编者并没有理解勾股定理证明的思路，只是根据一知半解的主观臆想将勾股定理的证明与相对论中的质能方程E=mc²联系了起来。

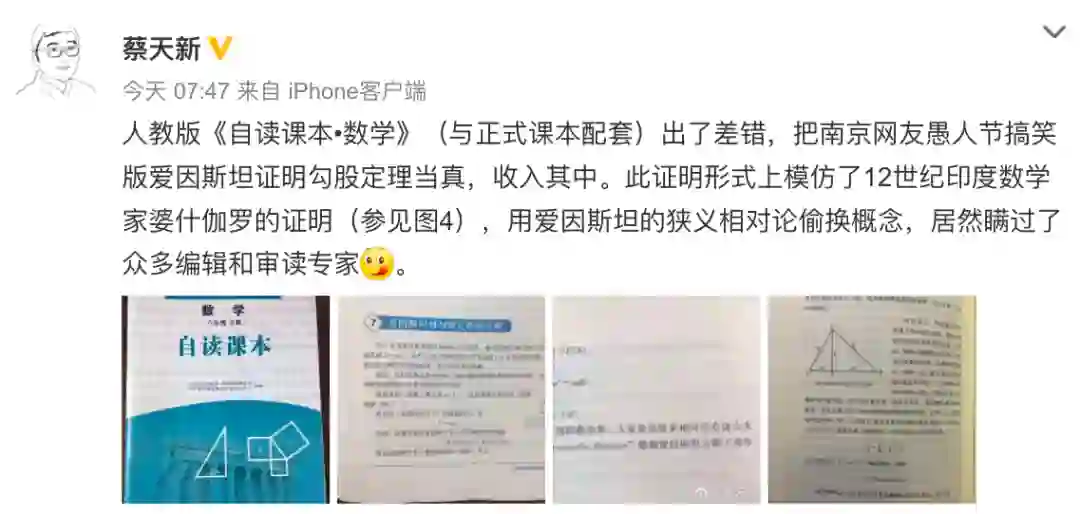
浙江大学的一位数学教授蔡天新表示，这一证明形式上模仿了12世纪印度数学家婆什伽罗的证明，用爱因斯坦的狭义相对论偷换概念。

一位网友表示，该部分内容看上去来源于一则陈年网帖，该帖文应该是作者在坛论中的玩笑帖，但是教材编者却当了真。

可以看出，2005年帖子原文和人教版数学自读课本里的推算差异不大，连爱因斯坦被聘任的轶事也一模一样。

       

据网购平台上的信息显示，编者为人教出版社课程教材研究所 中学数学课程教材研究开发中心。

澎湃社记者联系人民教育出版社工作人员后得知，这本自读课本不是教材，是供学生购买的课外辅助读物。工作人员表示出版社的确存在错误，稍后会发表声明。

 

参考链接：

https://www.zhihu.com/question/401988398

https://m.thepaper.cn/newsDetail_forward_7899766

https://user.guancha.cn/main/content?id=330124