一个想法：走向“纳什均衡”是普遍存在的大趋势

©作者 | coolmud

单位 | 中国移动研究院

研究方向 | 博弈论、机器学习

“纳什均衡”（Nash Equilibrium）是博弈（game）中一种特别状态：每个玩家单方面改变自己的策略（strategy）都不会有更好的收益。因此，所有玩家都会固守自己的策略，否则“不一定损人但一定不利己”，从而使得这个均衡状态具备一定的稳定性。1951 年，约翰·纳什就在数学上证明了均衡点存在。不过，虽然我们能体会玩家们不愿意离开均衡点，迄今为止却很少在现实世界中找到纳什均衡的存在，也找不到把玩家们推向均衡点的力量。事实上，玩家们实在没有理由主动去找均衡点而因此被困住。更重要的是，就算本着“公心”，在均衡点所有玩家收益总和还往往不是最高的。话句话说，在现实世界，无论是人类社会，还是广泛大自然，一个博弈要走向纳什均衡，要么有个超越于普通玩家的“协调者”在主动促成，要么是玩家们普遍的、不自觉的、简单的行为导致。 

我们先来排除协调者的可能性。首先协调者也没有动机搞什么“高大上”的纳什均衡，因为就算它能忍受不是最高的收益总和，也未必喜欢过于稳定而失去改变的能力。其次就是，协调者未必做得到。在玩家数量很多、策略数量也很多的情况下，协调者如何能够通悉所有玩家的收益情况？采用何种高效的算法？哪来的算力？要知道数学上可没有非常高效的算法，尤其是多人博弈。最后就是，回到刚才说的，就算协调者计算出均衡点，要为数众多的玩家通通欣然接受照做其策略也是一个大工程。因此，协调者的意愿不太可能是推动纳什均衡的动力。 

剩下的可能就是，在没有协调者的情况下， 玩家们的行为导致博弈走向均衡。假如真是这样，这种行为应该是玩家们普遍具备的，也应该是玩家本能驱动或者大自然规律强制的。因此，这个行为最终也应该是简单的，简单到每个玩家只需要看到自己的收益情况就能不断调整自身策略，而不需要考虑其他众多玩家的策略、收益情况，更不用关心均衡点在哪里。另外，简单意味着玩家们行为只需要极少的计算，最好是丁点都没有。 

而本文的主要观点就是，在现实世界玩家这种行为是普遍存在的，所以博弈走向纳什均衡是普遍存在的趋势。这种行为就是“平滑地、等比例地压制零遗憾策略”。

论文标题：

Geometrical regret matching: A new dynamics to Nash equilibrium

论文地址：

https://doi.org/10.1063/5.0012735

论文代码：

https://github.com/lansiz/eqpt

“平滑地、等比例地压制零遗憾策略”

这句话我们可以拆开来讲。先说说“零遗憾（regret）的策略”。假设某玩家具备三个策略 (A, B, C)，且该玩家使用纯策略获得的收益分别为20、-30、50，表示为 [20, -30, 50]。又假设在某次博弈中该玩家采用了混合策略，例如 (0.6, 0.3, 0.1)，那么玩家得到的收益是把混合策略当做概率分布进行计算：

当然，大家如果把上述混合策略当做股票投资组合 (60%, 30%, 10%)，可能比较有感。现在，看到 8 的收益，该玩家肯定最遗憾没有“满仓”策略 C、能挣 50，其次是比较遗憾没有满仓策略 A、能挣 20，最不遗憾满仓策略 B、挣负 30。可以看到，遗憾的程度刚好跟收益数值顺序一致，因此我们决定用纯策略收益来度量玩家对三个策略的遗憾程度，即 ： 。

同时出于后续的数学处理目的，我们希望把遗憾值控制在非负数范围内，也就是把 -30 换成 0，即零遗憾。那么就有： 。然而，因为收益数值是在实数范围内的，换负数为零的方法会轻易导致所有策略都是零遗憾，例如 。同样出于数学目的，我们把纯策略收益减去混合策略收益以保证至少有一个策略有正遗憾值：

这样我们得到了三个策略的遗憾值 <12, 0, 42>，其中策略 B 是零遗憾策略。刚才说到混合策略可以看作概率分布，因此零遗憾实质是标注了不高于期望收益的策略。 

现在可以说说“平滑地、等比例地压制零遗憾策略”了。 

回顾本文的目的，我们是希望，当所有玩家都迭代地、“平滑地、等比例地压制零遗憾策略”，博弈就奔赴均衡点。以上述初始混合策略 (0.6, 0.3, 0.1) 为例，为了满足“平滑地”、“等比例地”，我们这样设计那个玩家的混合策略调整方法：

上式中，我们实际上把 (0.6, 0.3, 0.1) 和 <12, 0, 42> 当作了三维向量。如下图所示，调整后的混合策略也是一个三维向量。相比向量 (0.6, 0.3, 0.1)，新的混合策略跟遗憾向量 <12, 0, 42> 的角度减小了，也就是被推向了遗憾向量。减小的角度受到正实参数 r 的控制，r 越小，角度变化越小。

下边红色箭头是调整后的混合策略

最重要的是，这种混合策略调整方法会同比例压制所有零遗憾策略，因为上式中分母一般是大于 1 的实数。举一个四个策略的例子可能更明显：当混合策略为 (0.6, 0.2, 0.1, 0.1) 、遗憾值为 (40, 0, 0, 20) 时，策略 B 和 C 对应比重都被同一个大于 1 的分母除，因此同比例减小了。 

然后，我们可以采用极微小的参数 r 来实现迭代调整的平滑。 

下文我们将演示，当所有玩家都按照上述方法迭代混合策略时，博弈将向均衡点演进。不过，在此之前，我们要解答本文最重要的一个问题：为什么“平滑地、等比例地压制不高于期望收益的策略”在现实世界是普遍存在的玩家行为？在市场中这个行为应该不难解释，符合玩家们“趋利避害”的本能习惯。在自然选择过程中，可以解释为，一个种群中采用劣势策略的个体数量被大自然逐渐消减。这其中，“等比例压制”是相对最苛刻的要求，需要玩家或者环境精确地执行。不得不承认，这个要求可能影响本文观点可信度。

均衡点逼近演示

从上面例子看到，无论是双人博弈，还是多人博弈，每个玩家只需知道自己的混合策略向量和纯策略收益向量，就能进行前述的策略调整。这个不可不谓简单，计算量并不大。但是，这时必须有个系统，对所有玩家提供它们各自的纯策略收益向量。准确地说，对任意玩家的任意混合策略 ，这个系统都能允许玩家获知收益 和纯策略收益向量 ，并且 必须为 和 的內积，即 。

举个例子。市场中，一个玩家以 (0.6, 0.3, 0.1) 的资金组合，分别获得了 [12, -9, 5] 的收益，因此容易计算出纯策略收益向量 [20, -30, 50]。这其中，市场本身必须对所有玩家提供上述信息。同此理，在自然选择中，大自然也扮演这样的系统。本质上，这个系统为每个玩家提供了一个函数，这函数必须同时输入其他玩家们的混合策略，计算后向该玩家提供信息。这个系统将承担主要的计算量。

下面进入演示环节。先是双人博弈的演示，然后是多人博弈。

为了演示双人博弈收敛到均衡点，我们就采用大家熟知的矩阵博弈中的 bimatrix 作为上述系统。综合前述的种种机制，我们可以这样实现双人博弈逼近均衡点的算法：

vertices payoff就是纯策略收益向量；max操作是对两个向量对等元素的逐个比较，并最终返回一个向量。

在上述算法会把混合策略的调整历史记录下来形成轨迹。对于 3×3 的双人博弈，轨迹肯定在二维的probability simplex上。为了直观，我们把simplex转换成平面上的等边三角形。

下面是三个典型示例的运行结果：

这个博弈只有一个均衡点，而且在均衡点两个玩家都会使用纯策略。

这个博弈只有一个均衡点，而且在均衡点两个玩家都会使用带有两个策略的混合策略。黑色叉叉是真实的均衡点。

有两个均衡点，每个均衡点的混合策略都使用两个策略。收敛到哪个均衡点取决于初始混合策略。

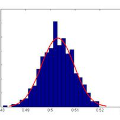
对于非 3×3 博弈，例如 60×40，因为混合策略向量超过三维，一定要可视化的话可以用 PCA 方法（主成分分析）减少维数到三维。例如：

一个60x40博弈

下面的示例演示了均衡点与初始混合策略是无关的。无论是什么初始策略，都会收敛到某个均衡点：

接着是多人博弈的演示。在本文使用的数学中，双人博弈只是多人的一种特例。因为在这两种博弈中，前述的信息提供系统都是以一个多变量联合概率分布为计算基础的，只不过双人博弈是两个变量的联合概率分布。

下面是一个多人博弈的示例：

这个博弈有6个玩家，每个玩家可以使用3个策略。

更代码多示例、详细数学机制见后文的“参考材料”。代码可以下载运行，有详细的操作方法。这里建议对多人博弈用好点的计算机运算。不然要等很久。

一个缺陷：混合策略“转圈圈”

就双人博弈而言，如果对随机生成的 3×3 或 4×4 博弈运行前述算法，会发现大约 25% 的博弈只有使用三个策略的均衡点可以作为收敛目标。这时候，混合策略轨迹就会转圈，而且转圈轨迹还不经过均衡点：

转圈的3x3

转圈的60x40

多人博弈就更严重了，大概率发生转圈。

转圈的成因见：

https://github.com/lansiz/eqpt#important-the-cyclic-strategy-path-issue

轨迹转圈会严重影响逼近均衡点的精度。这个问题目前没有办法解决。轨迹转圈可以简单理解为算法不断努力试图找到通向均衡点路径却始终没有路径可及、只能周而复始尝试。因此，博弈虽然没有最终逼近均衡点，但与走向纳什均衡的动力并不矛盾。

结论

纳什均衡可能是普遍存在的大趋势。这个趋势后面的驱动力就是玩家长期的行为习惯或者环境影响。这些驱动力因为简单所以普遍存在、因为贴近本能而难于抗拒。

我们现在能够想象到，纳什均衡的稳定性不但在于玩家喜欢呆在那里，还在于就算玩家偏离了均衡点也会被拉回均衡点。从这个意义上讲，纳什均衡像一个旋涡，玩家们被裹挟其中而不自知。

附1. 与纳什均衡存在性证明的关系

附2. 与“Regret Matching”方法的关系

附3. 随机生成“五人博弈”策略轨迹图（近500个示例图，40M）

网盘链接：

https://pan.baidu.com/s/12qzbApmndik3yhTCsjHOCA

提取码：

6666

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·