李飞飞点赞「ARM」：一种让模型快速适应数据变化的元学习方法 | 开源

鱼羊 编译整理
量子位 报道 | 公众号 QbitAI

训练好的模型，遇到新的一组数据就懵了，这是机器学习中常见的问题。

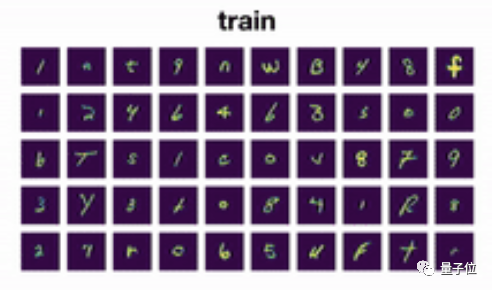
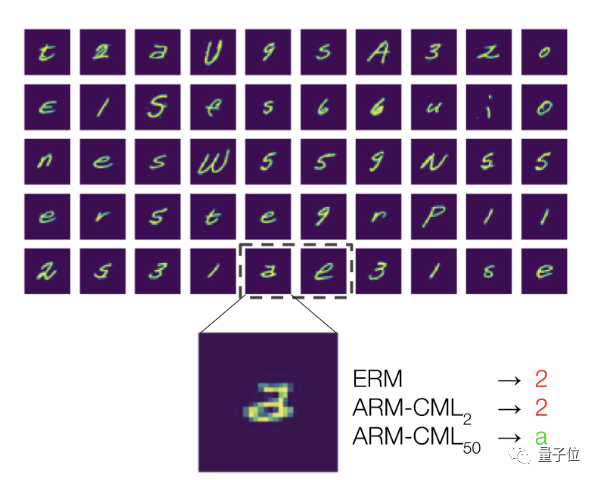
举一个简单的例子，比如对一个手写笔迹识别模型来说，它的训练数据长这样：

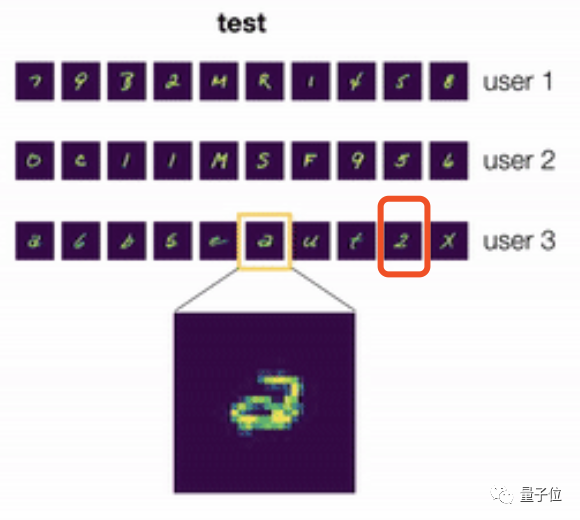
那么当它遇到来自另一个用户的笔迹时，这究竟是“a”还是“2”呢？

说实话，即使是人类，如果没看到该用户单独写了一个写法不同的“2”（图中红框），也很可能辨认失误。

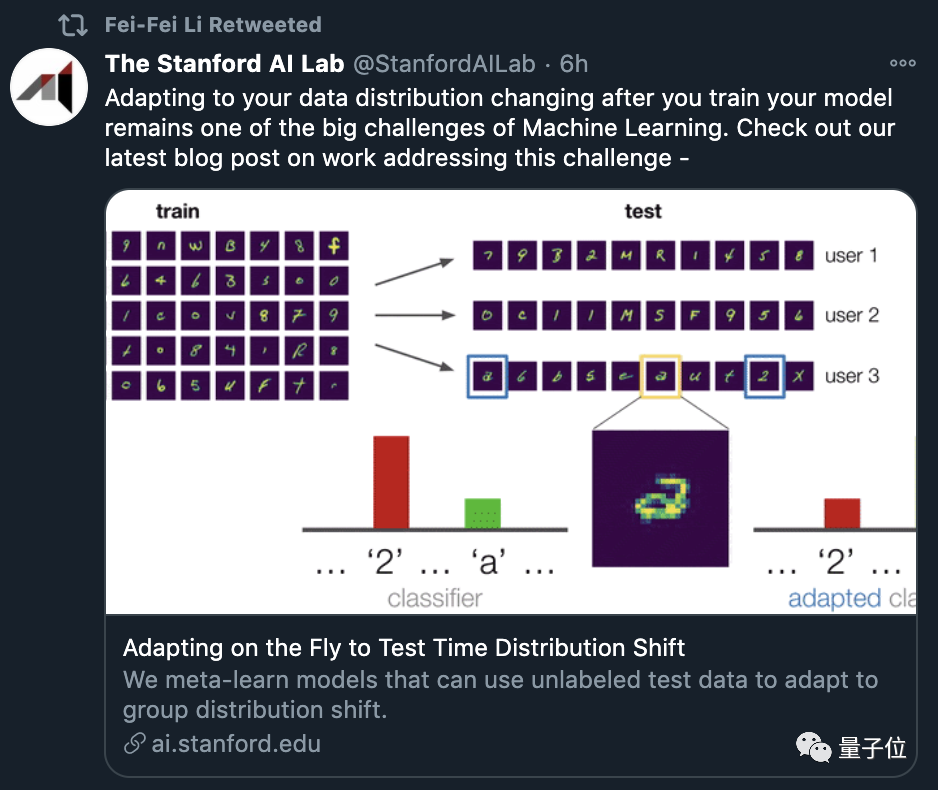
为了让模型能够快速适应这样的数据变化，现在，来自伯克利和斯坦福的研究人员，提出用元学习的方法来解决这个问题。

还获得了李飞飞的点赞转发。

不妨一起来看看，这一次元学习这种“学习如何学习的方法”又发挥了怎样的作用。

自适应风险最小化（ARM）

机器学习中的绝大多数工作都遵循经验风险最小化（ERM）框架。但在伯克利和斯坦福的这项研究中，研究人员引入了自适应风险最小化（ARM）框架，这是一种用于学习模型的问题公式。

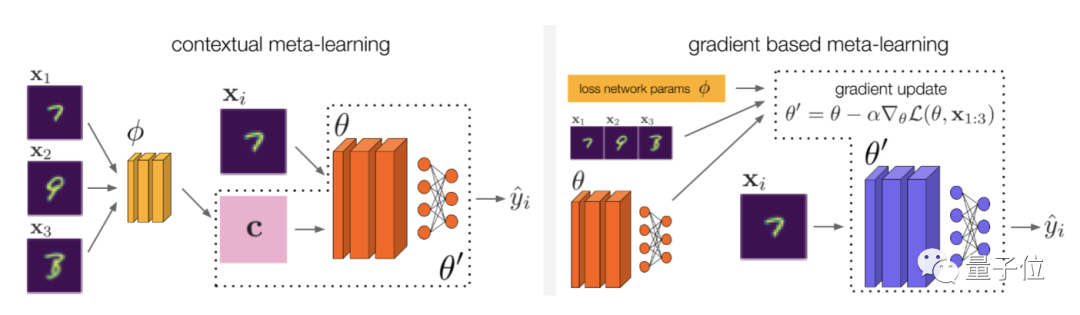
ARM问题设置和方法的示意图如下。

在训练过程中，研究人员采用模拟分布偏移对模型进行元训练，这样，模型能直接学习如何最好地利用适应程序，并在测试时以完全相同的方式执行该程序。

如果在测试偏移中，观察到与训练时模拟的偏移相似的情况，模型就能有效地适应这些测试分布，以实现更好的性能。

在具体方法的设计上，研究人员主要基于上下文元学习和基于梯度的元学习，开发了3种解决ARM问题的方法，即ARM-CML，ARM-BN和ARM-LL。

如上图所示，在上下文方法中，x1，x2，…，xK被归纳为上下文c。模型可以利用上下文c来推断输入分布的额外信息。

归纳的方法有两种：

• 通过一个单独的上下文网络

• 在模型自身中采用批量归一化激活

在基于梯度的方法中，一个未标记的损失函数L被用于模型参数的梯度更新，以产生专门针对测试输入的参数，并能产生更准确的预测结果。

优于基线方法

所以，自适应风险最小化（ARM）方法效果究竟如何？

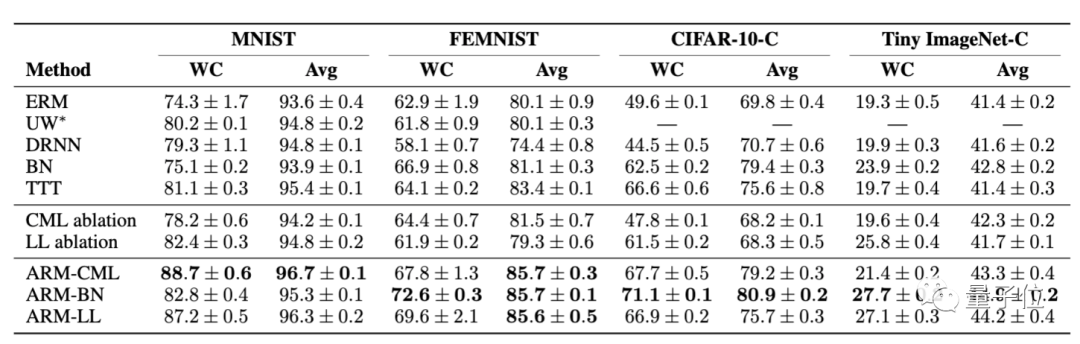
首先，来看ARM效果与各基线的对比。

在4个不同图像分类基准上的比较结果显示，无论是在最坏情况（WC）还是在平均性能上，ARM方法都明显具更好的性能表现和鲁棒性。

另外，研究人员还进行了定性分析。

以开头提到的“2”和“a”的情况举例，使用一个batch的50张无标注测试样本（包含来自同一用户的“2”和“a”的笔迹），ARM方法训练的模型就能够成功将两者区分开。

这就说明，训练自适应模型确实是处理分布偏移的有效方法。

这项研究已经开源，如果你感兴趣，文末链接自取，可以亲自尝试起来了~

传送门

论文地址：
https://arxiv.org/abs/2007.02931

开源地址：
https://github.com/henrikmarklund/arm

博客地址：
https://ai.stanford.edu/blog/adaptive-risk-minimization/

— 完 —

本文系网易新闻•网易号特色内容激励计划签约账号【量子位】原创内容，未经账号授权，禁止随意转载。

榜单征集！7大奖项锁定AI TOP企业

「2020中国人工智能年度评选」报名中！评选将从公司、人物、产品、社区四大维度共7个奖项寻找优秀的AI企业，欢迎大家扫码报名参与。 

评选报名截止于11.20，并将于12月16日揭晓，也期待与百万从业者们，共同见证这些优秀企业的荣誉！

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~