统计模型——《精通数据科学》

站在数据学科的角度, 融合数学、计算机科学、计量经济学的精髓.

If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.
如果有人不相信数学是简单的，那是因为他们没有意识到人生有多复杂。

——John von Neumann

下文节选自《精通数据科学：从线性回归到深度学习》, 已获异步授权许可, [遇见数学] 特此表示感谢! 

1.3 统计模型

从之前文章《什么是机器学习?》一文中可以看到，机器学习非常依赖所用的训练数据。但是数据就百分之百可靠吗？下面就来看两个数据“说谎”的例子。

如图 1-6 所示，我们将某 APP 每月的用户注册数表示在图中。图 1-6a 给人的直观印象是每月的安装数是大致差不多的，没有明显的增长。而图 1-6b 给人不同的印象，从 3 月份开始，用户注册数大幅度增长。但其实两幅图的数据是一模一样的，给人不同的感觉是因为图 1-6a 中纵轴的起点是 0，而且使用了对数尺度；而图 1-6b 的纵轴是从 17 000 开始的，而且使用的是线性尺度。

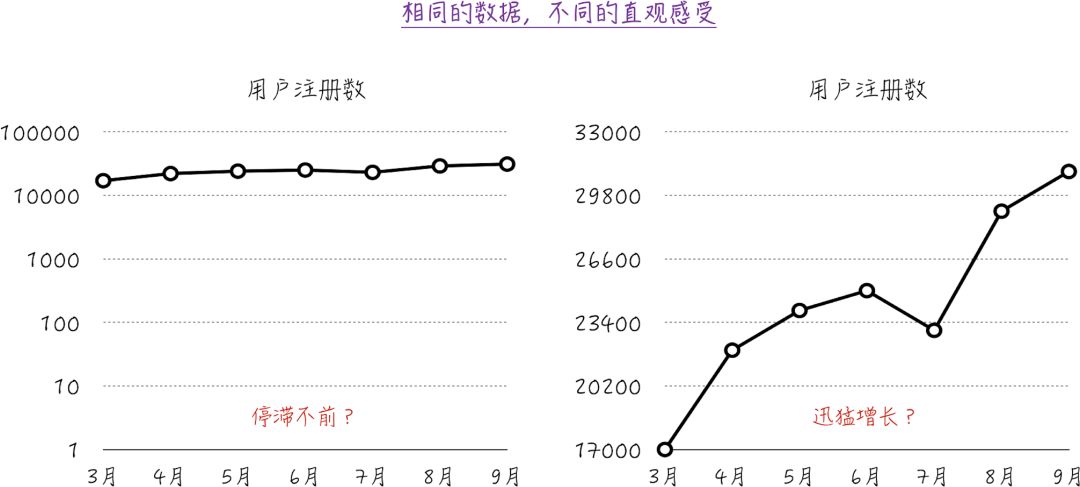
(a)                               (b)

读者可能会觉得上面这个例子太过简单了，只需要使用一些简单的统计指标，比如平均值或每个月的增长率，就可以避免错误的结论。那么下面来看一个复杂一点的例子。

当得到如图 1-7 所示的两组数据时，我们应该如何用模型去描述数据的变化规律呢？

● 对于图 1-7a，数据的图形有点像抛物线，因此选择二次多项式拟合是一个比较合理的选择。于是假设模型的形式为

y = (x-a)(x-b)

然后使用数据去估计模型中的未知参数a, b。得到的结果还不错，模型的预测值与真实值的差异并不大。

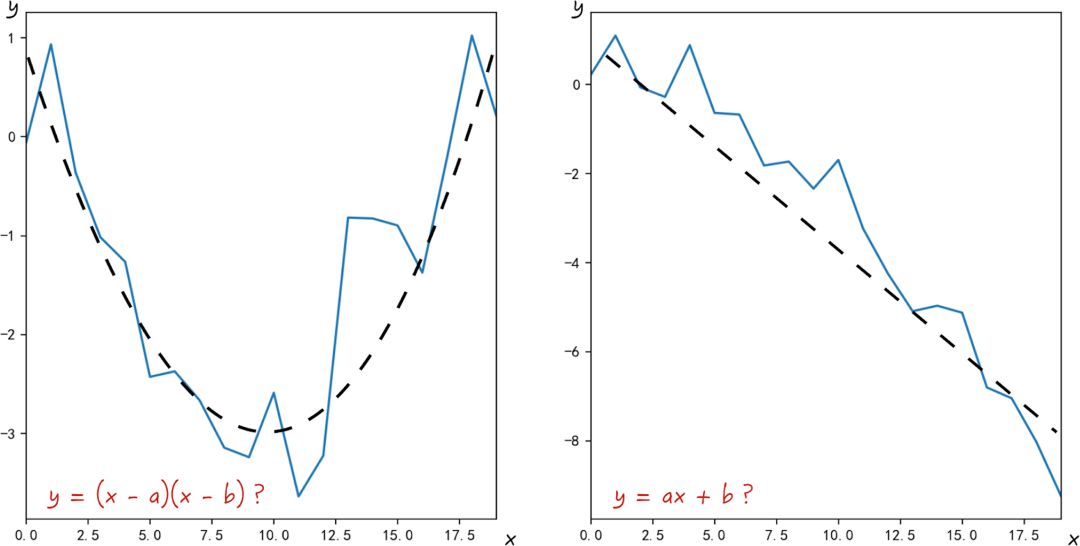
(a)                               (b)

● 对于图 1-7b，数据之间有明显的线性关系，所以使用线性回归对其建模，即

y = ax + b

与上面类似，得到的模型结果也不错。

根据上面的分析结果，可以得出如下的结论，图 1-7a 中的x与y之间是二次函数关系，而图 1-7b 的x与y之间是线性关系。但其实两幅图中的变量y都是与x无关的随机变量，只是因为观察窗口较小，收集的数据样本太少，让我们误以为它们之间存在某种关系。如果增大观察窗口，收集更多的数据，则可以得到完全不同的结论。如图 1-8 所示，如果将收集的样本数从20 增加到 200，会发现图 1-8a 中的数据图形更像是一个向下开口的抛物线，这与图 1-7a 中的结论完全相反。而图 1-8b 中也不再是向下的直线，而与开口向上的抛物线更加相似. 

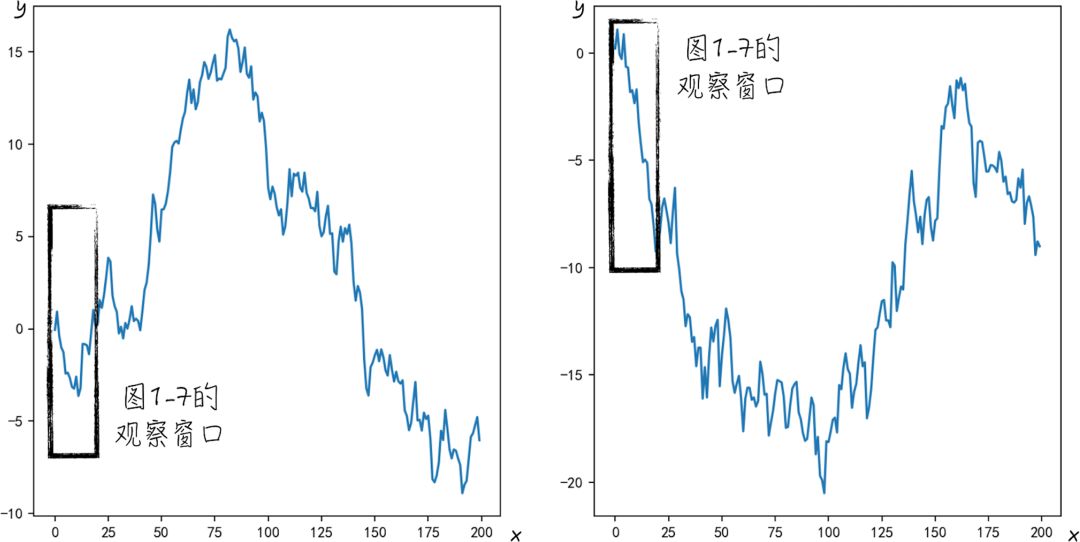
(a)                               (b)

上面的例子就是所谓的模型幻觉：表面上找到了数据变动的规律，但其实只是由随机扰动引起的数字巧合。因此在对搭建模型时，必须时刻保持警惕，不然很容易掉进数据的“陷阱”里，被数据给骗了，而这正是统计学的研究重点。这门学科会“小心翼翼”地处理它的各种模型，以确保模型能摆脱数据中随机因素的干扰，得到稳定且正确的结论，正好弥补机器学习在这方面的不足。

向上滑动阅览简介及目录 

作者者：唐亘
出版社：人邮出版社异步图书

长按上面二维码或
点击 【阅读原文】
跳转遇见微店购买

本书全面讲解了数据科学的相关知识，从统计分析学到机器学习、深度学习中用到的算法及模型，借鉴经济学视角给出模型的相关解释，深入探讨模型的可用性，并结合大量的实际案例和代码帮助读者学以致用，将具体的应用场景和现有的模型相结合，从而更好地发现模型的潜在应用场景。

本书可作为数据科学家和数据工程师的学习用书，也适合对数据科学有强烈兴趣的初学者使用，同时也可作为高等院校计算机、数学及相关专业的师生用书和培训学校的教材。

前言     

资源与支持     

第1章　数据科学概述     

第2章　Python安装指南与简介：告别空谈     

第3章　数学基础：恼人但又不可或缺的知识

第4章　线性回归：模型之母

第5章　逻辑回归：隐藏因子

第6章　工程实现：计算机是怎么算的

第7章　计量经济学的启示：他山之石

第8章　监督式学习： 目标明确

第9章　生成式模型：量化信息的价值

第10章　非监督式学习：聚类与降维

第11章　分布式机器学习：集体力量

第12章　神经网络：模拟人的大脑

第13章　深度学习：继续探索

1.4 关于《精通数据科学》

数据科学涉及计算机编程和数学建模这两个方面。它们之间的交集并不多，所强调的技能也有很大区别。这体现在实际生产中就是懂模型的人不懂编程，懂编程的人不懂模型，两者兼备的人才非常稀缺。本书的第一个目的就是将这两者的鸿沟弥补起来，注重模型假设和数学推导的同时，强调如何用代码实现模型。

• 从模型之间的联系和区别出发，分析各个模型的优缺点。帮助非数学专业的读者更加深入地理解模型的假设和适用范围，而不只是停留在会使用开源模型库的 API。

• 通过大量实际案例和代码展示，帮助非计算机专业的读者能独立上机实践模型算法， 而不只停留在模型的理论研究。对于数据科学中的模型搭建，统计学和机器学习是其最重要的组成部分。这两门学科的侧重点并不相同，在很多方面它们是彼此很好的补充。在面对一个实际问题时，若能将两者的方法相结合，能更好地挖掘数据的内在规律，从而更大程度地发挥数据的价值。这是本书的第二个目的。

• 将机器学习和统计结合起来，并借鉴统计学在经济领域的应用，为机器学习的算法提供一个生动而又不失精确的解释。同时用丰富的图片将这些解释直观地表现出来，帮助专业人员将模型和算法解释给非专业的业务人员，推动模型的落地和应用。

• 借鉴计量经济学的方法，深入探讨模型应用中常常被人们（特别是机器学习专业人员）忽略的问题，如模型是否稳定、模型结果是否可靠等，帮助读者反思建模过程中是否有考虑不周到的地方，以至于模型得到错误的结论。

当前，数据科学有两个最热门的前沿领域：分布式机器学习和深度学习。本书有专门的章节讨论它们，展示这两个领域想要解决的问题和目前最好（或最流行）的解决方案。这是本书的第三个目的：从宏观的角度向读者展示什么是数据科学，想要解决的问题、主要的方法以及未来的发展方向。

☟ 点击【阅读原文】进一步查看或购买此书