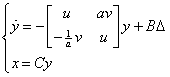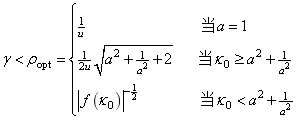【深度】东北大学王占山教授等：系统H∞范数计算：Lyapunov函数的直接优化方法

2019 年 10 月 11 日 中国自动化学会

CAA

智慧起航，共创未来

【导读】李雅普诺夫函数直接优化是指：针对系统H无穷范数问题，通过求解最优李雅普诺夫函数，给出系统H无穷范数的通用解析表达式，实现系统H无穷范数的直接和精确求解。

刘秀翀, 王占山. 系统H∞范数计算:Lyapunov函数的直接优化方法. 自动化学报, 2019, 45(8): 1606-1610.

H无穷控制理论主要是用来解决系统存在外部扰动情况下的优化控制问题。在H无穷控制理论研究范畴，无论是鲁棒控制还是鲁棒优化控制，最终影响系统性能的还是闭环系统的特征根或传递函数零极点的分布。因此，研究这一分布对系统性能的影响是H无穷控制理论的基础。在H无穷控制理论中，传递函数(或系统)的H无穷范数是一项重要的性能指标，用于度量扰动输入对系统输出的影响，反映了闭环系统的抗扰能力。在H无穷控制理论研究中，长期存在一个挑战性课题：能否基于系统参数，直接构造出系统H无穷范数的精确解析表达式。

H无穷控制理论最初是从频域入手进行研究，并在1989年转换到时域，进而开启了基于状态空间方程描述的系统的H无穷性能研究。目前，求解H无穷范数的主流方案是：将H无穷范数求解问题转化为时域状态空间的约束优化问题。典型的方法为：基于有界实引理给出的线性矩阵不等式(LMI)约束条件，近似寻优H无穷范数的解。这类LMI方法的优点在于能够得到较高精度的H无穷范数估计，其存在的不足表现为：

1）这类方法只能得到H无穷范数估计的数值解，而无法得到解析解；

2）这类方法无法揭示系统结构和参数对系统H无穷性能的影响，在一定程度上限制了控制器精细设计的研究。

为了克服上述不足，就要从改变求解H无穷范数的途径入手。事实上，LMI类方法求解H无穷范数的途径是：给定一个H无穷范数估计，并判断LMI约束条件中李雅普诺夫函数矩阵的存在性；通过不断减小该估计值近似寻优H无穷范数。因此，LMI类方法暗示了一个前提：难以(或无法)直接构造出一个与H无穷范数相对应的最优李雅普诺夫函数。如果这一前提能够突破，即基于系统参数能够直接构造出这样一个最优李雅普诺夫函数，则系统H无穷范数解析表达式的构造就具有可行性。这样求解H无穷范数的途径就可以改变，进而克服LMI类方法存在的不足。

鉴于二阶系统是控制系统中应用最广泛、最具代表性的系统之一，并且多数高阶系统在一定的条件下可以近似(或分解) 为二阶系统来研究，同时为有效展现最优李雅普诺夫函数与系统参数存在的内在关系，本文针对一类二阶线性系统的H无穷范数问题，尝试直接构造一个与H无穷范数相对应的最优李雅普诺夫函数，进而给出基于系统参数的H无穷范数精确解析表达式。

如何构造一个最优李雅普诺夫函数？尽管最优李雅普诺夫函数与系统参数存在内在关系，但这种关系是复杂和非显性的。因此，直接基于李雅普诺夫方程或参数化黎卡提不等式，难以找到这种内在关系并构造出适合的李雅普诺夫函数。这是早期研究结果存在保守性的根源。为解决这一问题，本文的工作如下：

1）采用状态空间转换技术，将原系统转换为H无穷范数等价的新系统（这一转换提取出系统特征参数，并使构造一个最优李雅普诺夫函数具有可行性）；

2）在新的状态空间研究系统，建立参数化黎卡提不等式；

3）构建含有待优化参数的通用李雅普诺夫函数；

4）基于该参数化黎卡提不等式，以H无穷范数估计最小为优化目标，优化李雅普诺夫函数中的参数，进而得到基于系统特征参数的李雅普诺夫函数，用于精确分析系统H无穷范数。

如何构造系统H无穷范数的通用解析表达式？应用新状态空间下的黎卡提不等式和所构造的李雅普诺夫函数，本文针对状态空间转换所得到的二阶系统

构造出基于系统特征参数的H无穷范数精确解析表达式

其中f(•)是由系统参数确定的函数。

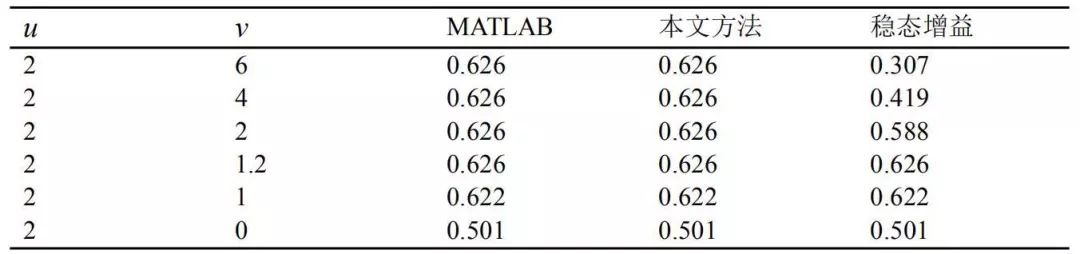
表1在不同系统特征参数条件下，给出了不同方法所得结果。表1表明，采用H无穷范数解析表达式给出的结果具有较高精度。

表1 H无穷范数分析（a=2）

目前，关于李雅普诺夫函数最优化问题的研究尚处于萌芽阶段，相关的尝试和探索（尤其是针对高阶线性和非线性系统）还有待发展。本文针对系统H无穷范数求解问题，提出了一种李雅普诺夫函数的直接优化方法。通过直接优化黎卡提不等式中的李雅普诺夫函数，构造出基于系统特征参数的H无穷范数解析表达式。本文的研究展现了系统特征参数对系统H无穷性能的影响，避免了H无穷范数求解中复杂的数值优化过程，为H无穷控制理论的研究提供了一个新的思路。

作者简介