【机器学习】最大熵马尔科夫模型

2020 年 2 月 3 日 AINLP

本文介绍了最大熵马尔可夫模型，在隐马尔可夫模型（隐状态序列）的基础上应用最大熵模型思想，将一个概率生成模型转化为概率判别模型，同样最大熵马尔可夫模型带解决的三个问题：1）概率计算，2）参数学习，3）序列预测，其中概率计算与参数学习类比于最大熵模型，序列标注采用维特比解码。

作者 | 文杰

编辑 | yuquanle

最大熵马尔科夫模型

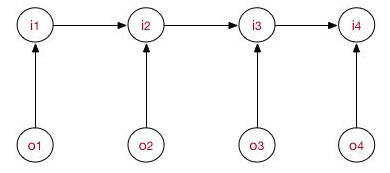
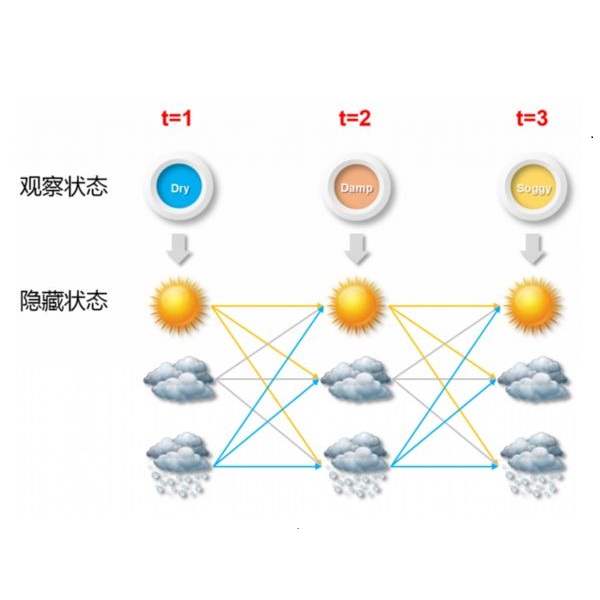
有最大熵模型和隐马尔可夫模型的基础，再看最大熵马尔科夫模型就直观多了。在隐马尔可夫模型中:

即与之间独立作用。在最大熵马尔科夫模型中则没有这一假设，而直接采用条件概率的形式输出模型。

结合最大熵模型，不考虑整个序列时，第时刻的状态可以看作是一个分类问题，采用最大熵模型，由和，构成分类模型，有最大熵模型的结论，我们知道分类模型是一个关于的函数，表达式如下：

其中是联合标签特征模板，是特征模板的权重，是联合所有可能的标签特征模板求和，表示归一化因子。对于参数的求解，可以采用最大熵模型的使用的优化算法，但是值得注意的是，在优化求解过程中，每个时刻单独归一化，不考虑序列性。

这里，由于笔者之前的误解，对于最大熵模型的特征模板的概率求解采用最大似然估计的方式直接对特征模板进行统计，以其频率作为概率，结果发现还是有效。其中原因可能是我的这种统计方式是基于期望最大化的思想，运用最大似然估计得到模型参数正好是统计频率。

在状态预测中，考虑最大化整个序列的概率，意味着目标函数如下：

目标函数也就是求解一条最优的状态转移路径，同样可以采用Viterbi算法。

代码实战

A、最大熵模型维特比算法

int Viterbi_M(const DataStr &testdata)  {  int t,i,j,k;  int pos;  double deta[VEC_LEN][STATE];  int fai[VEC_LEN][STATE];  double max_deta;  double max_fai;  int max_i;  for(i=0; i<STATE; i++)  {  pos=getPos(testdata[0][0]);  deta[0][i]=dicos_m.ps0[i]*dicos_m.pos[pos][i];  fai[0][i]=0;  }  for(k=0; k<testdata.size(); k++)  {  for(t=1; t<testdata[k].size(); t++)  {  for(i=0; i<STATE; i++)  {  max_deta=double_min;  max_fai=double_min;  for(j=0; j<STATE; j++)  {  pos=getPos(testdata[k][t]);  if(deta[t-1][j]*dicos_m.pss[j][i]*dicos_m.pos[pos][i]>max_deta)  {  max_deta=deta[t-1][j]*dicos_m.pss[j][i]*dicos_m.pos[pos][i];  }  if(deta[t-1][j]*dicos_m.pss[j][i]>max_fai)  {  max_fai=deta[t-1][j]*dicos_m.pss[j][i];  max_i=j;  }  }  deta[t][i]=max_deta;  fai[t][i]=max_i;  }  }  max_deta=double_min;  for(i=0; i<STATE; i++)  {  if(deta[testdata[k].size()-1][i]>max_deta)  {  max_deta=deta[testdata[k].size()-1][i];  max_i=i;  }  }  cout<<max_i;  for(t=testdata[k].size()-2; t>=0; t--)  {  max_deta=double_min;  cout<<fai[t+1][max_i];  for(i=0; i<STATE; i++)  {  if(deta[t][i]>max_deta)  {  max_deta=deta[t][i];  max_i=i;  }  }  }  cout<<endl;  }  }

完整代码见阅读原文。

The End

本文转载自公众号：AI小白入门，作者文杰

推荐阅读

AINLP年度阅读收藏清单

鼠年春节，用 GPT-2 自动写对联和对对联

大幅减少GPU显存占用：可逆残差网络(The Reversible Residual Network)

征稿启示| 让更多的NLPer看到你的文章

AINLP-DBC GPU 云服务器租用平台建立，价格足够便宜

我们建了一个免费的知识星球：AINLP芝麻街，欢迎来玩，期待一个高质量的NLP问答社区

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLP君微信(id：AINLP2)，备注工作/研究方向+加群目的。