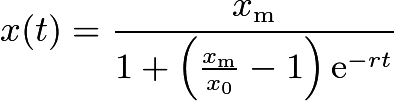将数学内化成为自己的思维

本文参与遇见数学＃ 数学蒲公英 ＃征文活动，作者赵梦瑶 。 ★ 提示: 如果文中数字/公式显示较大, 请点击右上角中"刷新"即可恢复正常. 

    

如果不是搞数学科研领域或从事有关数学专业的人，大多都会觉得数学在日常生活中并没有太多的直观的实用价值。可能多数人会觉得平时的消费购物只需要 100 以内的加减法就足够了，至于微积分、导数、圆锥曲线、拉格朗日中值定理……对于大多数人来说实用性并不大。这句话本没有问题，当一个人从事与数学毫无关联的工作时，那些数学定理与数学证明就会渐渐被遗忘。

然而，数学作为基础学科，作为中考、高考的三大主科之一，学子在数学领域经历十年寒窗苦读的目的究竟是什么？作为一个数学爱好者，我所追求的不仅仅是教材上的数学定理与数学证明，而是尽可能地去探究每一个公式定理背后所隐藏的逻辑关系，将数学真正内化成为属于自己的思维。随着这种思维的形成，就会慢慢发现，在生活中，太多太多的科技成就，比如当今社会比较热门的机械自动化生产、人工智能等领域都映射着数学的影子，展现着数学的价值。

所以，当把数学思维真正内化成为自己的思维习惯的时候，你的思考问题的方式及处理问题的方法就会变得不一样，全面而缜密。而在学习、工作和生活中，这种思维方式发挥着举足轻重的作用。即使是过了10年，20年，30年……公式定理会有遗忘，但这种经历数学学习而不断提炼总结而留下来的思维方式会使你终身受益，这便是数学核心素养最终的体现。它会使你面对困难的时候，能够多角度地看待并理性的分析。

在小学、初中以至高中阶段，求解数学题目往往有唯一正确的答案。但当把数学真正内化成为自己思维，具有足够思想深度的时候，对于数学建模的求解却没有唯一答案。对于同一个问题可以建立多种不同的数学模型，它并没有绝对的正确与错误之分，此时，实践就作为了评价模型优劣的唯一标准。

▲ 托马斯·罗伯特·马尔萨斯, 他的《人口学原理》影响深远  (图自维基)

比如：在对人口预报问题进行建模分析的时候，可以建立马尔萨斯人口模型。

假设人口增长率  是常数。记时刻  时人口数为 ，时刻  的人口为 ，由于量大，可视为连续、可微函数， 到  时间段内人口的增量为 

满足微分方程：

  (1)

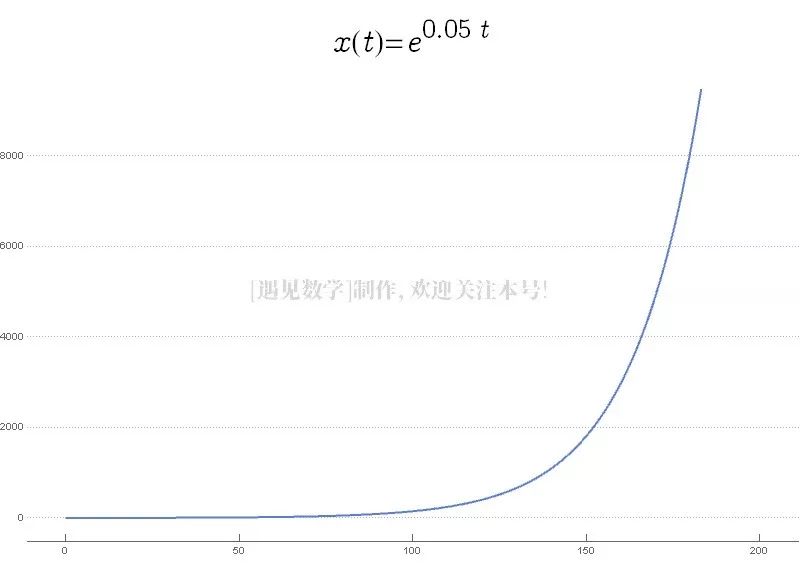
解微分方程(1)可得: (2)

这表明  时，，此模型说明人口将以指数规律无限增长，而实际上，随着人口的增加，自然资源、环境条件等因素对因素对人口增长的限制作用越来越显著。

而 logistic 模型 就可以对指数增长模型关于人口净增长率是常数的假设进行完善。

假定 （线性函数） 为固有增长率，自然增长资源和环境条件年容纳的最大人口容量为 

当 时，增长率应为 ，即 ,于是 ,代入 ，得

 (3)

将（3）式代入（1）式可得模型：

 (4)

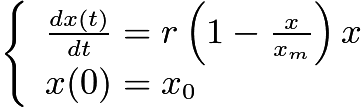
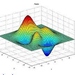
解方程（4）得 
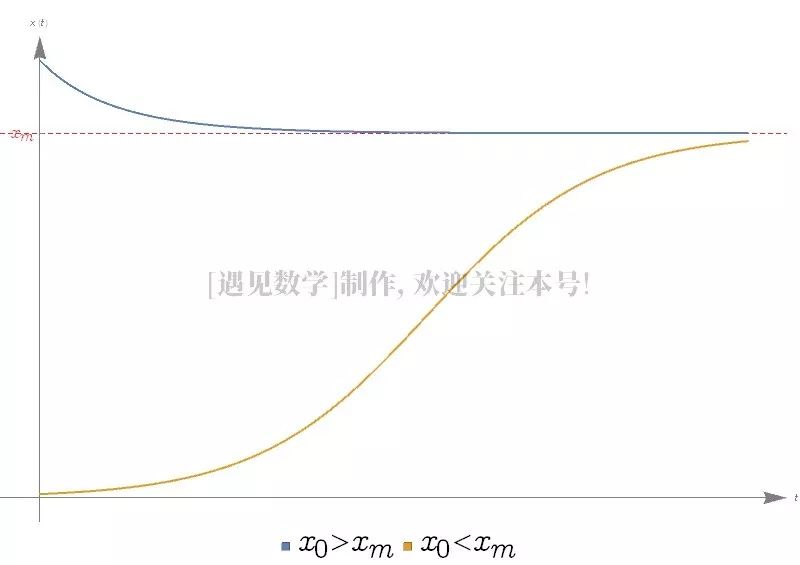
由此还可以作出  曲线，由图像可看出人口数随时间的变化规律。

日常生活中，类似于这样的数学模型还有很多，比如：投资的受益和风险问题，最短路径问题……这样来看，数学不仅是解决实际问题的有力工具，更是一次深度的思考与理性的冒险。

通过多种途径去探索数学，再将数学内化成为自己的思维，学会把握数学所特有的符号语言与图形语言，华罗庚曾言道“数缺形时少直观，形缺数时少入微”图形语言也正是数学最高级的语言。

以导数为例，我们通常借助函数图像可以更加直观的看出导函数的正负，由此得出原函数的增减（单调性），随之发现函数的极值，最值，零点，参量的范围等结论和规律，进而找到解题的关键点。综上分析，导数解题最核心、最本质的策略就是数形结合。透彻的理解这一点，导数便不再成为我们的绊脚石。

不懂得深度的思考，从外界获取再多的知识与学问也都是一纸空谈。内化的过程，正是自我反思，自我提高，自我升华的的过程。只有经历这个过程，才能真正转化成为自己的东西，才能创造出新领域的科技产品。

将数学内化成为自己的思维，这也正是数学的学科意义所在。善于从实际生活中抽象出数学模型，从已知领域到未知领域的探索，让思维实现质的飞跃。无论什么时候，无论发生什么，永远要怀揣着对数学最澎湃的热情，因为内化成为的属于自己的思维是一种数学素养。(完)

参考文献：
赵静，但琦，数学建模与数学实验（第4版），高等教育出版社，2014年8月。

作者赵梦瑶，现就读于天和城实验中学 高三年级 理科实验班，担任学生会宣传部副部长，荣获校级优秀干部。指导教师：罗学礼。
青春宣言：没有一条路无风无浪，会有孤独，会有悲伤，也会有无尽的希望。