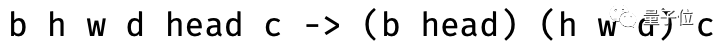ICLR 2022 Oral | 这个工具开源三年后，终于中顶会了！

点击下方卡片，关注“CVer”公众号

AI/CV重磅干货，第一时间送达

博雯 发自 凹非寺
转载自：量子位（QbitAI）

那个在GitHub标星4.3k的张量操作工具Einops，在开源三年后终于中了顶会！

这是一个统一的、通用的操作张量结构的方法，基于爱因斯坦求和约定（Einstein summation convention）的思路开发，能够大幅提高代码的可读性和易修改性。

同时，Einops支持Pytorch、TensorFlow、Chainer、Jax、Gluon等多个深度学习框架，以及Numpy、Cupy等张量计算框架。

ICLR 2022将其接收为Oral论文的消息一出，无数白嫖多年的“精神股东”们纷纷奔走相告，认为Einops确实“当之无愧”：

不过，这一早就声名在外，还有无数大牛站台的工具，在投往顶会后却并非一帆风顺。

比爱因斯坦求和约定更好用的标记法

我们先来了解一下Einops的基本原理。

它的设计思路来自于爱因斯坦在1916年提出的爱因斯坦求和约定，也叫爱因斯坦标记法（Einstein notation）。

这一方法的规定是：当一组乘积中，有两个变量的脚标一样，就要对相同的两个脚标求和。例如下图中的a_ib_i：

这样书写的好处是，避免公式里出现大量的求和符号，看起来更简洁。

Numpy里的Einsum就是一种模仿爱因斯坦求和约定的方法，可以说，这种思路已经被广泛使用。

而Einops正是基于Einsum进行了诸多改进，针对张量操作过程中一些以前难以解决的问题，提供了更加便利的方案。

比如，当仅通过Pytorch，以及结合Einops两种方法来实现超分辨率（Super-resolution）时，后者无疑极大降低了代码冗余：

△上：原版 下：结合Einops

可以看到，结合了Einops之后的代码不需要特殊指令PixelShuffle，并且，还使用了模块调用nn.ReLU以及nn.Sequential。

最后得到的输出结果既不包含虚假坐标，还能在框架之间进行转移。

为什么Einops能做到这些？

这得益于Einops的本质：这是一种针对变换模式的新的标记法，能够确保元素在张量中的位置与坐标变量的值一对一映射。

△Numpy和Einops操作之间的对应关系

对比爱因斯坦求和约定（Einsum），Einops有几个额外的特征：

• 减少仅存在于输入中的坐标（例如可以使用max-reduction法）

• 重复仅存在于输出中的坐标（张量值对于新坐标的索引都是一样的）

• 使表达式两边的所有坐标的标记唯一（Einsum允许重复）

在这些特征中，输入和输出被描述为张量的维度和坐标的预期顺序，这使得基于Einops的代码的可读性和易修改性非常高，用户也不需要在每次操作后记住或推断出张量的形状。

同时，Einops将输入坐标（或其组成）与输出坐标连接起来，这也使得张量结构在设计上就无法被破坏。

用括号表示的坐标的组成和分解也是Einops的一个主要创新之处：

通过上述的特点，Einops模式有利于更加灵活地处理高维度数据。

比如，一个注意力机制函数接受了一个形状为[batch，seq，channel]的张量k q v，Einops可以将其高度、宽度和深度合成为一个维度。

同时，张量的头部和batch维度也能够被分组，这就保证了注意力头部的独立处理，从而将其变为三维数据的多头注意力：

类似的，通过修改输入和输出的结构，其他神经块也能够在Einops模式下完成“升级”。

论文接收并非一帆风顺

Einops的作者是来自俄罗斯的Alex Rogozhnikov，他拥有莫斯科大学的数学和物理学博士学位，目前的主要研究领域是机器学习。

而Einops正是他最火热的一项开发，不仅在GitHub上收获4.3k星，还有特斯拉AI高管、FAIR实验室工程师站台：

但是，当作者将其整理成论文并投稿顶会时，有不少审稿人认为这篇论文“读起来像是一篇技术博客”、“创新性不够”、“缺乏严谨性”，并给出了3分（拒绝）的意见：

不过，会议主席最终给出了一锤定音的正面评价，并同意将其接收为Oral论文。

比起将几个模块共同训练、压缩、结合，最后在某个任意基准上的SOTA增加0.31 +/-1.04，这篇论文所描述的技术对于ICLR读者来说更重要。

有Einops的使用者专门将会议主席最后的评价贴了出来，并表示：

除了新颖的技术和SOTA之外，其他的很多论文也同样具有价值。

而不管这篇论文有何更广泛的鼓励意义，至少对于开发者Alex Rogozhnikov本人来说，也算是修成正果了。

论文：
https://openreview.net/forum?id=oapKSVM2bcj

GitHub链接：
https://github.com/arogozhnikov/Einops

作者主页：
http://arogozhnikov.github.io/about/

ICCV和CVPR 2021论文和代码下载

后台回复：CVPR2021，即可下载CVPR 2021论文和代码开源的论文合集
后台回复：ICCV2021，即可下载ICCV 2021论文和代码开源的论文合集
后台回复：Transformer综述，即可下载最新的3篇Transformer综述PDF

CVer-Transformer交流群成立

扫码添加CVer助手，可申请加入CVer-Transformer 微信交流群，方向已涵盖：目标检测、图像分割、目标跟踪、人脸检测&识别、OCR、姿态估计、超分辨率、SLAM、医疗影像、Re-ID、GAN、NAS、深度估计、自动驾驶、强化学习、车道线检测、模型剪枝&压缩、去噪、去雾、去雨、风格迁移、遥感图像、行为识别、视频理解、图像融合、图像检索、论文投稿&交流、PyTorch和TensorFlow等群。

一定要备注：研究方向+地点+学校/公司+昵称（如Transformer+上海+上交+卡卡），根据格式备注，可更快被通过且邀请进群

▲长按加小助手微信，进交流群

CVer学术交流群（知识星球）来了！想要了解最新最快最好的CV/DL/ML论文速递、优质开源项目、学习教程和实战训练等资料，欢迎扫描下方二维码，加入CVer学术交流群，已汇集数千人！

▲扫码进群
▲点击上方卡片，关注CVer公众号

整理不易，请点赞和在看