证明ABC猜想：意义重大，却无人能识？

2017 年 9 月 16 日 算法与数学之美

2012年8月30日，43岁的日本数学家、京都大学教授望月新一在数学系主页上贴了4篇论文，通过总共长达512页的艰深推理（当代数学论文多为10~20页），他宣称自己解决了数学史上最富传奇色彩的未解猜想：ABC猜想。

望月新一

ABC猜想在27年前由Masser和Oesterlé分别独立提出。自那时以来，鲜有数学家敢于尝试证明它的正确性，而先前号称自己证明了该猜想的人，经由数学界检查，他们的证明也都因各种错漏而被否认。望月新一解决难题的能力广为人知，所以数学界必定会认真研究他的论文，从全局的思维过程到最细枝末节的精巧构造，就正确与否给出一个答案。

但是，问题来了：谁能看得懂这套证明，并且明白证明背后建立起来的新数学理论的哲学？James D. Taylor在著名数学论坛MathOverflow上发了一个帖子，很多数学家，包括菲尔兹奖得主陶哲轩和望月新一的好友、牛津大学教授金明迥也参与了讨论；最后大家得出的答案是：没人看得懂。

现代数学研究的机制已经趋于成熟，一个问题总是基于前人的工作和对相关问题的理解而提出的，解决问题的机制也多为已知方法的变种。2003年，佩雷尔曼证明了统一人类对三维宇宙认识的庞伽莱猜想，用的是上世纪80年代汉密尔顿引入微分几何的研究方法“Ricci曲率流”；几百年前费马声称空白太窄写不下证明过程的费马最后定理，怀尔斯爵士在上世纪上世纪80年代证明该猜想时，用的也是上世纪50年代建立起来高阶椭圆曲线的模形式理论。

克莱因曲面的模曲线

望月新一遇到的情况却有点不同。他已经在ABC猜想的证明工作上独自思考了20年，建立起了他称之为“宇宙際Teichmüller理論”的新世界，定义了各种前所未有的神秘术语，比如第一篇论文讲了“霍奇影院”（Hodge Theater）的构造，第二篇论文则引入了“外星算数全纯结构”（alien arithmetic holomorphic structures）。

代数几何和数论领域的大多数资深数学工作者都认为，望月的理论过于玄妙，不值得花上几年时间去仔细阅读，弄清楚新定义的术语、推理的脉络和理论的结构。诚然，最坏的可能是，到头来大家发现这个新理论把自己绕进了死胡同；当然，最好的结果是，望月的证明建立起了新的数学分支，将代数几何和数论统一起来。

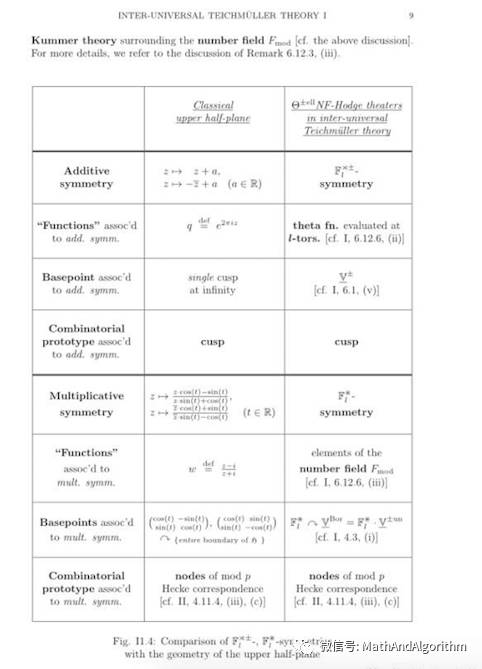
望月论文中宇宙際Teichmüller理論的定义和数论中传统概念的比较

ABC猜想到底在猜测什么？

读者们，你们即将经历数学中最为抽象、仿佛起源于虚无的数论和代数几何的结合体。这里的理论无法用图示去说明，是在把解方程这件事情综合分析得出“对称”、“互质”之流的结构之后，进一步抽象得到的结构的结构。

简单来说，就是有3个数：a、b和c =a+b，如果这3个数互质，没有大于1的公共因子，那么将这3个数不重复的质因子相乘得到的d， “几乎一定”会比c大。举个例子：a=2，b=7，c=a+b=9=3*3。这3个数是互质的，那么不重复的因子相乘就有d=2*7*3=42>c=9。大家还可以实验几组数，比如：3+7=10，4+11=15，也都满足这个猜想。

但是，上面所述之内容，并非猜想的全貌，而且依照上面的算法去找a+b=c，还居然存在反例！著名的ABC@home 网站就在用分布式计算寻找ABC猜想的反例，其中一个反例是3+125=128：其中125=5 ³ ，128=2 ⁷ ，那么不重复的质因子相乘就是3*5*2=30

这就是ABC猜想的表述了，听起来好像不如以前我们知道的数论中的猜想那样精确直观。比如费马最后定理：a ⁿ + b ⁿ = c ⁿ ，当n大于等于3时就没有整数解了。又比如哥德巴赫猜想：一个数一定表示成两个质数之和。ABC猜想不但涉及加法（两个数之和），又包含乘法（质因子相乘），接着还模糊地带有点乘方（1+ε次方），最坑爹的是还有反例存在？这实在有点山寨——如果你这样想，那就太小瞧这个猜想了。实际上，除了尚未解决的涉及多个数学分支的猜想界皇冠黎曼猜想以外，与ABC猜想的影响力相比，其他数论中的猜想，诸如哥德巴赫猜想、孪生质数猜想，以及已经解决的费马最后定理，都只能算是战斗力只有5的渣滓。

ABC猜想为何如此重要？

首先，ABC猜想，对于数论研究者来说，是反直觉的。

历史上反直觉的却又被验证为正确的理论，数不胜数。一旦反直觉的理论被证实是正确的，基本上都改变了科学发展的进程。举一个例子：牛顿力学的惯性定律，物体若不受外力就会保持目前的运动状态，这在17世纪无疑是一个重量级的思想炸弹。“物体不受力当然会从运动变为停止”，这是当时的普通人基于每天的经验得出的正常思想。而实际上，这种想法，在任何一个于20世纪学习过初中物理、知道有种力叫摩擦力的人来看，都会显得过于幼稚。但对于当时的人们来说，惯性定理的确是相当违反人类常识的！

ABC猜想之于现在的数论研究者，就好比牛顿惯性定律之于17世纪的普通人，更是违反数学上的常识。这一常识就是：“a和b的质因子与它们之和的质因子，应该没有任何联系。” 原因之一就是，允许加法和乘法在代数上交互，会产生无限可能和不可解问题，比如关于丢番图方程统一方法论的希尔伯特第十问题，早就被证明是不可能的。如果ABC猜想被证明是正确的，那么加法、乘法和质数之间，一定存在人类已知数学理论从未触及过的神秘关联。

质数螺旋

再者，ABC猜想和其他很多数论中的未解问题有着重大联系。

比如刚才提到的丢番图方程问题、费马最后定理的推广猜想、Mordell猜想、Erdős–Woods猜想，等等等等。而且，ABC猜想还能间接推导出很多已被证明的重要结果，比如费马最后定理。从这个角度来讲，ABC猜想是质数结构的未知宇宙的强力探测器，仅次于黎曼猜想。

其次，我们来看望月用了什么数学工具来解决ABC猜想。

望月开始埋头研究ABC猜想的证明时，距猜想提出不过10年，而且几乎没有任何进展，望月可以说是几乎从零开始的。之所以说 “几乎”，是因为望月20多岁时，在“远阿贝尔几何”[1]领域中作出过超卓贡献，还被邀请到4年一届的国际数学家大会上演讲。然而，1988年柏林的数学家大会结束之后，望月就从学术界消失，潜心于他自己的宇宙去证明ABC猜想了。他用的理论工具，正是“远阿贝尔几何”。

可以说，望月证明ABC猜想的目的之一，就是要把远阿贝尔几何发扬光大。远阿贝尔几何这个数学分支，由代数几何教皇格罗腾迪克于上个世纪80年代创建，研究对象是不同几何物体上的代数簇的基本群的结构相似性。

在富有传奇色彩的丽沃夫咖啡馆，近代分析学之父巴纳赫说：“数学家能找到定理之间的相似之处，优秀的数学家能看到证明之间的相似之处，卓越的数学家能察觉到数学分支之间的相似之处。最后，究级的数学家能俯瞰这些相似之处之间的相似之处。” 格罗腾迪克，便落入了巴纳赫分类的究级数学家之列，远阿贝尔几何便是一门研究“相似之相似”的数学分支： 16世纪，的卡尔达诺研究3次方程求根；19世纪，伽罗瓦发现特殊高次方程解的群结构；代数几何中的代数簇，则是一大类方程的公共解；代数簇的基本群，则是对于已经综合了一大类理论的代数簇理论的再一次综合，关心什么样的结构独立于几何物体的代数簇的表象之外。

球射影空间上的代数簇

于是乎，对于数学家来说，检查望月的证明是否存在错漏的另外一个难题就是：要透彻理解望月那512页的ABC猜想的证明，需要先弄懂望月关于远阿贝尔几何的750页的著作！全世界总共只有约50名数学家在这方面有足够的背景知识去通读望月这本远阿贝尔几何著作，更别提望月在证明猜想中建立起来的“宇宙際Teichmüller理論”了。目前为止，自称“宇宙際幾何學者”的望月，是他自己创造出的宇宙中的独行者。

之前提到的望月的好友、牛津大学教授金明迥说：“读证明，对数学家来说，也是非常痛苦的。说服大多数代数几何学者去阅读需要如此之多基础知识的证明，更是一件难事。” 当然，这并不代表没有数学家在检查望月的证明，2012年10月，斯坦福大学教授Akshay Venkatesh函至望月，指出第3篇和第4篇论文中的错误。望月也迅速答复，承认了错误，并说明该错误对整体理论并无影响。

证明发表之后，怀疑之声不绝于耳。因为从直觉上来讲，ABC猜想如果被证明正确，对于数论的影响之巨大，无异于相对论和量子物理之于现代物理学。有些人认为，要是ABC猜想被证明，世界就太美好了，仿佛身处幻境。

大多数数论工作者希望，望月能够就他的证明写出一个综述，将整套理论的逻辑脉络展现给大家，比如为什么要引入定理X和概念Y，怎么层层推进到最终猜想的证明。设立千禧年大奖的克雷数学研究所也在考虑邀请望月开办一个讨论班，邀请世界上最优秀的数论和代数几何学家参加，大家一同学习这个新理论。

不过，关于望月新一本人，他在发布证明之后拒绝了任何采访，而且他不喜好社交。在Google上搜索关于望月新一的背景介绍，中文链接中可读的，唯有卢昌海发布在他个人主页上的文章：“望月新一 1969 年 3 月 29 日出生于日本东京， 16 岁进入美国普林斯顿大学就读本科，三年后进入研究生院，师从著名德国数学家、 1986 年菲尔茨奖得主法尔廷斯， 23 岁（即 1992 年）获得数学博士学位。此后，他先是、‘海归’ 成了京都大学数理解析研究所的研究助理，几个月后又前往美国哈佛大学从事了近两年的研究，然后重返京都大学。 2002 年， 33 岁的望月新一成为了京都大学数理解析研究所的教授。望月新一的学术声誉颇佳，曾获得过日本学术奖章等荣誉。”

关于望月的这种出世的行事方法，金明迥作出的评价是：“当你沉浸在自己的理论宇宙中太久，你会察觉不到他人对于你的理论的困惑，因为你先入为主地假设了所有人都明白很多基础知识。”

故事到此就告一段落了，大家都在见证历史。

来源：数学与人工智能

☞ 深度神经网络中的数学，对你来说会不会太难？

☞ 编程需要知道多少数学知识？

☞ 陈省身——什么是几何学

☞ 模式识别研究的回顾与展望