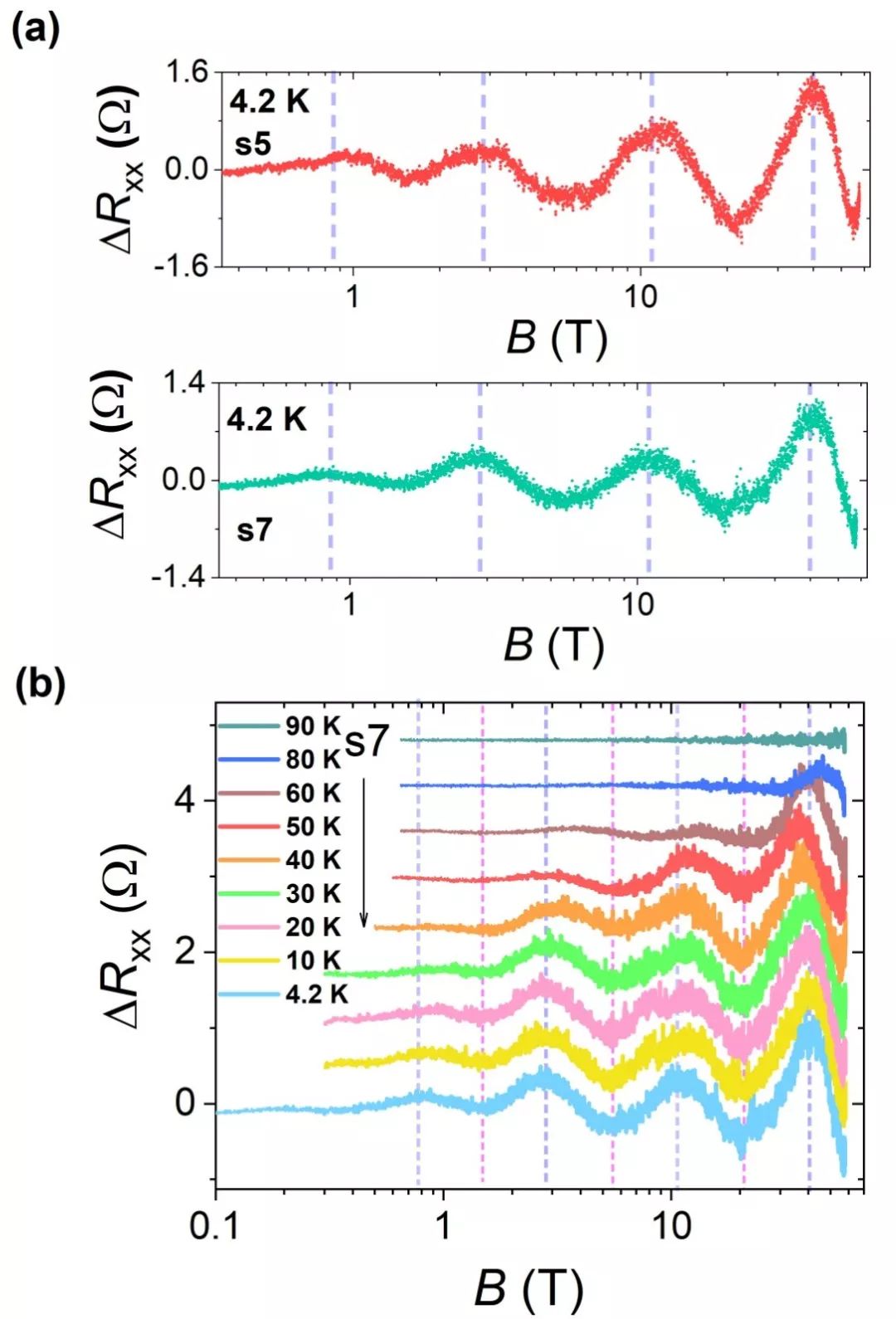
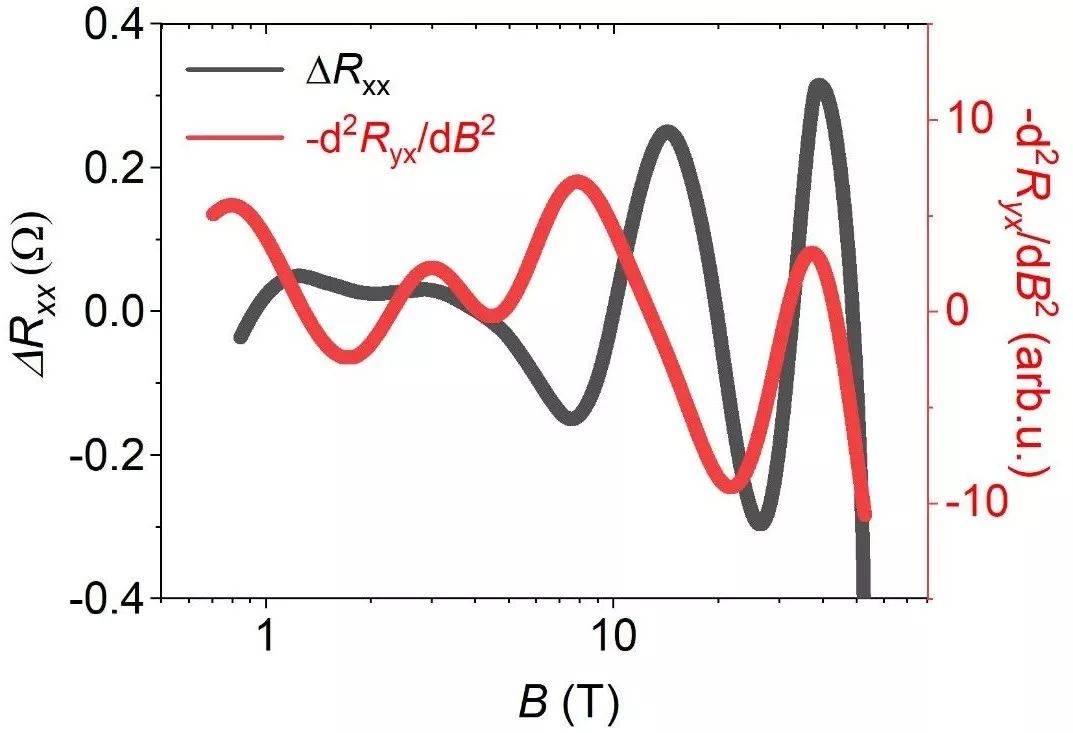
HfTe5中的对数周期量子振荡：在狄拉克材料中观测原子塌缩现象 | NSR研究论文

海归学者发起的公益学术平台

分享信息，整合资源

交流学术，偶尔风月

2018 年，北京大学王健教授与谢心澄院士等合作，在拓扑材料ZrTe₅中发现了一种全新规律的量子振荡——对数周期磁阻振荡（Science Advances 4(11), eaau5096, 2018）。这一工作揭示了固体材料中目前仅知的第三种周期性的量子振荡，因而受到广泛关注。

 

最近，一篇发表于《国家科学评论》(National Science Review，NSR) 的文章报道，外加磁场下，在拓扑材料HfTe₅单晶的纵向电阻和霍尔电阻上均可观测到对数周期量子振荡，这表明对数周期量子振荡不局限于ZrTe₅体系，可在狄拉克材料中普遍存在。

 

固体材料中的对数周期量子振荡为何重要？

因为这种振荡是体系中准粒子发生原子塌缩现象，并伴随出现离散标度不变性的结果。

超临界塌缩是相对论量子力学理论的重要预言，然而由于自然界中缺乏超重原子, 这一现象尚未得到实验直接证实。 离散标度不变性是连续标度对称性破缺的结果，体系的特征尺度满足等比数列，因而呈现对数周期性。 离散标度不变性体现在地震、湍流、金融危机等多个研究领域。 在物理学领域内，冷原子领域的Efimov三体束缚态已观测到离散标度不变性，然而固体材料体系中的离散标度不变性极为罕见。

狄拉克材料中的准粒子满足相对论性方程, 并且其体系的精细结构常数远大于真空中取值，因此是在凝聚态体系中观测超临界原子塌缩现象和离散标度不变性等量子现象的理想平台。

本研究中，研究者在最高58 T的脉冲强磁场下系统性测量了拓扑材料HfTe₅单晶的电输运性能。如下图（a）所示，不同样品的纵向磁电阻都表现出明显的对数周期量子振荡。进一步的变温实验表明，该体系中，温度达到80 K以上时对数振荡才会消失。

                           

(a)纵向磁电阻中的对数周期量子振荡。

(b) 不同温度下的磁电阻振荡。

 

更重要的，研究者还实现了对数振荡在霍尔结果中的首次观测，这表明离散标度不变性广泛存在于不同的输运系数之中。而且，同一样品中磁电阻和霍尔电阻的对数周期量子振荡具有一致的周期，并存在一个稳定的相位差。

同一样品中，纵向磁电阻和霍尔电阻中的对数周期振荡周期一致且存在相位差。

 

基于上述实验结果，研究者进一步揭示了其背后的物理机制。在HfTe₅中，无质量的狄拉克粒子受到库仑吸引，从而形成满足离散标度不变性的准束缚态。在外加磁场下，准束缚态的能级逐个经过费米面，并对费米面处的载流子引起散射，导致电阻发生对数周期的振荡。

 

此外，磁电阻和霍尔电阻中对数振荡相位差的存在，说明对数振荡来自费米面附近的共振散射，这种情形类似于二维体系中整数量子霍尔效应中所存在的相位差。

 

这一最新发现表明对数周期量子振荡和离散标度不变性在狄拉克材料中存在普适性，有助于深入理解固体系统中这些新奇的现象。北京大学王健教授、北京师范大学刘海文研究员、香港理工大学戴吉岩教授为论文共同通讯作者，王慧超博士与博士生刘彦昭为共同第一作者。

论文信息

Huichao Wang,  Yanzhao Liu,  Yongjie Liu,  Chuanying Xi,  Junfeng Wang, Jun Liu,  Yong Wang,  Liang Li,  Shu Ping Lau,  Mingliang Tian,  Jiaqiang Yan, David Mandrus,  Ji-Yan Dai,  Haiwen Liu,  X C Xie,  Jian Wang

Log-periodic quantum magneto-oscillations and discrete scale invariance in topological material HfTe ₅

National Science Review, nwz110, 

https://doi.org/10.1093/nsr/nwz110

点击左下角“阅读原文”查看论文原文。

扩展阅读

 

量子振荡的新篇章：对数量子振荡的发现

北大发现三维拓扑狄拉克半金属中的非常规超导特性

量子材料大观园(3) | Ising专栏

复旦大学首次观测到量子自旋液体中的分数化激发

本文系网易新闻·网易号“各有态度”特色内容

媒体转载联系授权请看下方