数学弱则芯片无:数学与芯片工业
01、半导体简介
半导体工业是目前我国薄弱并且最重要的工业之一, 半导体也是现代人生活中不可或缺的工业产品, 电话、音响、计算机、汽车, 甚至玩具和电饭锅里面都会有半导体, 不过当大家在讲半导体时, 往往还不太清楚什么是半导体, 什么是半导体呢? 首先我们先来看1945年物理学诺贝尔奖得主包利(W. Pauli) 在1932年写给他同事的一段文字:
On semiconductorsone should not do any work, that is a mess, who knows whether there aresemiconductors.
这段文字充分地显示出当时对「半导体」这个物理现象是非常模糊的, 其实半导体还没被人们发现之前它只是一些不值钱的石块, 可是当人们学会怎么利用它时, 它却变得如此的重要; 我们可以这样说: 「半导体是一堆不值钱的石头」, 我们也可以这样说: 「半导体是非常有价值的东西」; 之所以会有这样矛盾的结果出现, 是因为半导体的材料是一种具双重性质的物质, 它可以是一种导体也可以是一种绝缘体, 而到底是导体还是绝缘体? 取决于半导体工业界中最重要的两件事(A 与B 事件):
A、What is done to it?
B、How to control the current?
这两个动作可以说是点石成金, 如果加了该加的东西, 再加上知道怎么控制电流(Current),那它就会变成半导体; 相反的,它就是一块没有用的石头, 以下是科学百科全书对半导体的诠释:
Asemicondutor is a material that can behave either as a conductor or aninsulator depending on what is done to it.
We cancontrol the amount of current that can pass through a semiconductor.
现在我们来看一下半导体的历史发展,法拉第(Michael Faraday, 1791-1867) 是第一个注意到有半导体这种材料的人, 法拉第的发现很多, 最有名的是磁可以转化为电的电磁感应现象。这里我们要讲的则是法拉第较少为人所知的一项发现, 那就是他在公元1833年发现硫化银(Silver Sulfide) 的电阻与普通的金属不同, 它的电阻随着温度的上升而降低, 而普通金属的电阻都是随着温度的上升而增加的。半导体从1833年被Faraday 发现后, 其中经历相当多的屈折故事, 事实上在发现后近一百年内, 科学家对半导体现象仍存在有截然不同的正反见解,也就是说半导体从发现到完全被证实足足有一百多年之久, 可见半导体的奥妙与艰深难懂, 但是近年来半导体的发展却是相当的快速, 从1969年第一颗包含一个晶体管(Transistor) 的芯片(Chip) 被发明至今, 短短的五十年之间, 技术已经可以做到把超过两千万个晶体管放到同一片芯片上了。以下为半导体在发展上所发生的一些大事:
1833 –Faraday discovered semiconductivity in Ag2S
1841 –Hittorf showed Faraday wrong
1902 –Straints showed Faraday right
1911 –Koenigsberger and Weiss termed “semiconductor”
1920 –Juband showed Faraday wrong
1933 –Wagner showed Faraday right
1935 –Gudden “Si is not a semiconductor”
1947 –Bardeen, Brattain, Shockley discovered transistor
1962 –First semiconductor laser
1969 –Single transistor on one chip
1999 ~Over 1010 transistors on one chip
02、半导体组件与半导体工业的发展
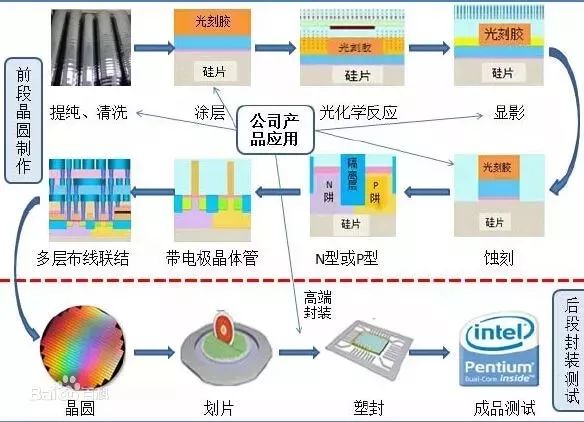
现在我们来看一些半导体组件以及近年来半导体工业是如何的发展, 首先我们先来看一下半导体组件是如何产生的, 一般来讲,半导体组件的产生需要通过晶圆、黄光、切割等· · ·几个步骤, 如图一所示。
半导体的主要材料是从石头或砂子中萃取出硅, 经高温溶化成99.9%的纯硅铸块(Ingot), Ingot 长得像一个纯银色的不锈钢圆柱, 经钻石锯切割后成一块块直径为4、6或8吋大的晶圆(Wafer), 经过消毒、磨光后的晶圆像一面光滑的镜子, 每一块晶圆最后将含上百个相同的芯片(Chip), 这些芯片就是我们去计算机零售商购买的微处理器(Micro Processor) 或易失存储器(DRAM)。
芯片的制造过程大致如下: 首先晶圆需经过化学沉淀、扩散以及离子植入方式使其带正电,此谓掺入杂质(Doping), 然后此带正电晶圆再置入一个1200℃的烘炉内烘烤氧化而在表面形成一层不导电的氧化层(Dioxide), 然后再铺上一层胶固状的不透光体(Photoresist), 接着一片铺陈着复杂集成电路设计图的模版置于此晶圆上, 经过紫外线照射使Photoresist依设计图路径被软化,此谓光罩(Mask); 之后再置于黄光室将软化的Photoresist 清除, 接下来再把Dioxide部份用热气蚀刻(Etching) 掉而形成电路信道, 这些信道再Dope 成带负电的硅化物,最后信道与信道之间再铺上一条条铝(或铜) 线使其相连成一个完整的集成电路IC (Integrated Circuit), 此步骤叫Interconnect,图二是IC 最基本的示意结构之一。
上述的这些步骤通常会重复好多次, 因此晶圆上一层一层的IC 图被铺设起像一层层大楼被建造起来, 再经过切割、封装、测试后成为一片片像姆指甲大小般的Chip。
这个产业从设计、制造、光罩、封装到测试等过程, 皆有专业公司负责而形成一个紧密且高效率的垂直整合工业团队也是一个重要的因素。
图一. 半导体简要制造过程
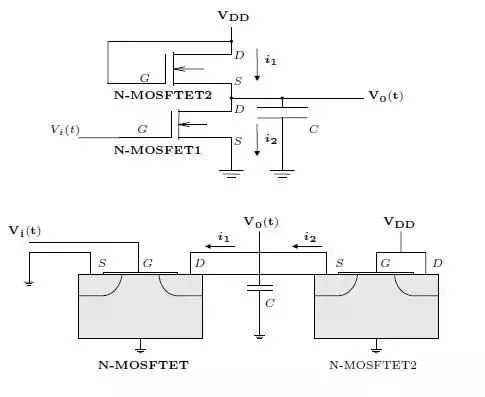
图二. Metal-Oxide-Silicon Field Effect Transistor
现在我们来看看一个最基本的IC 结构:
MOSFETInvertor (反向器), 如图二, 图中Vi 是输入电压, V0 是输出电压, 如果MOSFET(在纯硅上加了不同的杂质后的半导体,A 事件) 的导电特性适当, 我们则可控制(B事件) i1 与i2 的电流大小进入而控制电容C 使其充电或不充电(0或1计算机的基本运算于焉开始)。
上面的集成电路里, 每一个MOSFET组件, 就长得如图三:
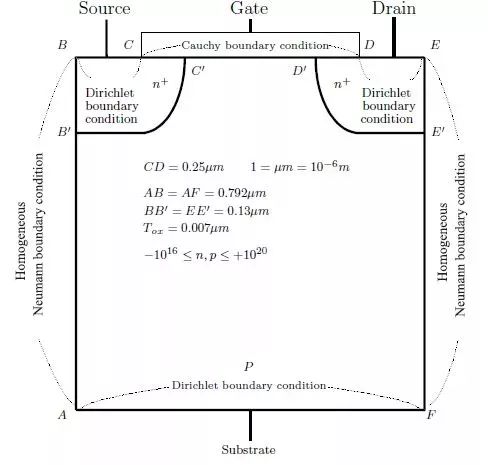
图三. MOSFET 基本组件
当不同电压加在S(Source), G(Gate),D(Drain) 时, 我们希望电子(负电荷) 能有效地从C′跑到D′ 而使S 与D 间通电, 当CD 的距离愈小时, 组件的尺寸就愈小, 现在已经可以量产10纳米的组件了, 这里10纳米就是代表CD 的距离也就是导电线的线宽。
03、半导体数学简介
半导体数学其实是指半导体物理与工程中相关的数学问题, 而半导体物理是探讨半导体特性的学科, 需要用到以下几种物理课程:
1、基础物理
2、近代物理
3、量子力学
4、固态物理
5、统计力学
主要的观念是守恒率、运动方程式、电场、电荷; 而在半导体数学方面主要是专门处理半导体的模式与分析, 用到了以下几种数学:
1、微积分
2、高等微积分
3、实变函数
4、泛涵分析
5、微分方程
6、数值分析
7、统计
8、概率
研究主题含模式推导、数学性质、模式的求解、以及用计算机来仿真组件物理特性; 而这些简称为半导体数学为什么要存在于半导体工业中呢? 我们可以从它的制作过程:「沙子」→ 晶圆→ · · · → 封装→ 切割→ 贩卖, 这整个点石成金术可不是三天两夜就变的出来的,从最原始的硅元素,到IC 芯片,起码需要花三个月的时间才能成就一颗有价值的IC,在这段漫长的时间里, 有数以百计的程序需要被处理, 只要其中有一步骤稍微出了差错,就全功尽弃,因此, 如果我们能先透过半导体数学的模拟计算, 来预测某个条件下, 组件所具有的物理特性, 我们便能快速的找出最适合某类组件的组成系数, 就能节省开发新组件所需的成本, 这样的好处在越往小组件发展, 所节省的成本就越明显, 可以看出半导体数学在制作过程中所占居的位置。
从1969 年第一颗包含一个晶体管(Transistor) 的芯片(Chip) 被发明至今, 短短的五十年间, 技术已经可以做到把超过两千万个晶体管放到同一片芯片上了。随着半导体产业的突飞猛进, 组件的尺寸越来越小, 晶体管的数目越来越多, 相对的研发的成本也越来越高, 在此情况下, 想要对每一种设计理念, 包括不同的组件尺寸(Device Geometry)、组件材质(Device Material)、不同的偏压(Bias)、以及制程技术中的微影(Lithography)、参杂(Diffusion、Implantation)· · · 等, 都加以实际实验是非常不实际的, 其付出的成本可以说是天文数字, 因此就有人把数学引进半导体业界, 主要分成组件仿真(Device Simulation) 和制程模拟(Process Simulation),以下主要讨论组件仿真的部分, 希望能以数学的方程式来描述半导体的特性。但是此时就会遇到两个无法避免的难题:
1. 如何找到可以描述半导体特性的数学方程式?
2. 如何找出这些方程式的真正解?
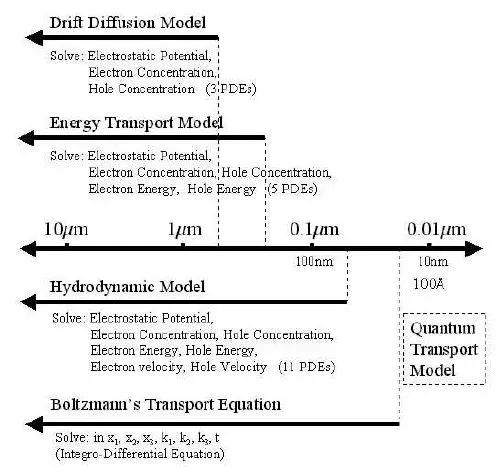
对于第一个问题, 经由数学家和物理学家的不断努力下, 现在已找到了许多可以描述半导体特性的方程式, 下面列出一些可以描述半导体特性的方程式及其所适用的组件大小(约略尺寸):
1、Drift Diffusion Model (大于0.7μm)
2、Energy Transport Model (大于0.3μm)
3、Hydrodynamic Model (大于0.07μm)
4、Boltzmann’s Transport Equation (大于0.03μm)
5、Quantum TransportModel (可用于小于0.01μm)
图四. 适用于不同组件尺寸的数学模式
一般来讲较上方的方程式是由下方的方程式做了一些关键性的假设或忽略所得到的,但随着组件的大小渐渐的变小, 这些可以简化方程式的假设也变得不成立了, 所以越下方的方程式其复杂度会远远超过上方的, 对此我们可以依据组件的大小来选择所需的方程式, 以免大才小用。
至于第二个问题, 很不幸的答案是没有方法, 对于工程界有兴趣的问题, 现今的数学并没有方法求得这些方程式的真正解, 那怕是最简单的Drift Diffusion Model 都没有办法, 更不要说是Boltzmann’s Transport Equation 或Quantum Transport Model了。相信大家一定会觉得很奇怪, 既然没有办法解这些方程式, 那如何把数学带进半导体产业呢? 虽然数学没有办法解出真正的解,但借由数值方法和高运算能力的计算机, 我们可以得到近似的解,只要近似解够接近真正解, 我们就可以用此近似解来当作实验所得的数据, 如此就可以把一些不良的设计在此阶段就先加以剔除。但是随着方程式的逐渐复杂化, 如今连想要求得近似解的难度也越来越高了, 对此我们只有期望能有新的方法来计算这些方程式, 及更快速的计算机能早日被发明出来以满足呈爆炸性成长的计算量。
04、半导体数学模型的意义
在上面, 依组件尺寸的大小, 我们看到了相当多的数学模式可以用来描述半导体特性, 在这里我们选择最基本的Drift Diffusion (漂移扩散)Model 来简略地看看这些数学方程式的物理意义:
DriftDiffusion Model:
(1)Δφ=q/εs*(n − p + D)
(2)∂n/∂t=∇*(Dn∇n)−∇*(μnn∇φ)+R
(3)∂p/∂t=∇* (Dp∇p)−∇ * (μpn∇φ)+R
对这三个方程式, 我们想要寻求三个未知函数(φ, n, p) 的解, 这里n 代表在图三正方形区域ABEF 内的电子浓度(单位面积内电子的个数), 如果ABEF 依摩尔定律一路往下缩小, 我们可以想象将来的组件只有一个电子, 的确, 这即是目前科学界非常重要的研究课题之一「单电子晶体管」, 高中化学我们学过原子最外层能阶的电子可能受外在环境影响而逃脱原子的束缚而在物质晶格上游走(即漂移), 因此n 是代表这批“游离”电子的浓度, 如果原子没办法留住它的电子而任其游走天涯(形成电流), 原子将带正电荷我们称之为电洞, 而p 即代表电洞的浓度。电学最基本的定律库伦定律告诉我们带电的东西A(如电子本身) 会形成一个电场E, 而E 对另外一个带电的东西B 形成有位能φ存在的现象, 电位能与电场的关系是E = − (位能变化) / (位置变化) 以二维空间而言
E = −∇φ= −(∂/∂x,∂/∂y)φ= −(∂φ/∂x, ∂φ/∂y)
这里∂φ/∂x即代表φ在x 方向变化的情形。
ABEF 内的电子浓度由于受到外加电场(φ的边界条件) 以及我们在纯硅上加了不同的物质(A 事件, Doping) 而有所变化,这即是D 在(1) 式右边的意义, q 是基本电荷常数, "s 是介电系数, 也是常数而(1) 式即代表电场因电子在不同位置有不同数量而产生的变化, 即−∇E 等于q/εs*(n − p + D)对φ而言, (1) 式是φ的二阶偏微分方程式,即
Δφ= ∇∙∇φ=(∂/∂x,∂/∂y)∙ (∂φ/∂x, ∂φ/∂y)=∂2φ/∂x2+∂2φ/∂y2
现在我们来看看第二个式子, 此式称之为电子连续方程式, 是依据质量不减定律算来的, 为了简化起见, 我们把问题放在一维空间来考虑, 想象x 轴是一条密度不均匀的河流(电子流;高速公路上的车流), 其流速在x 点t 时间时为v 向东流去, 令Q 代表单位时间内通过x 的电子数, 考虑电子流在某一线段I = (x, x + Δx) 的情形:∫x x+Δx[n(s, t +Δt) − n(s, t)]ds: 表示在时段Δt 内电子在I 的增加总数量, [Q(x, t)−Q(x + Δx, t)] Δt: 表示在_t时间内电子流入与流出I 的总数量, ∫x x+Δx (R(s, t )Δt) ds:表示电子在I 与Δt 内因碰撞或与电洞相结合而得的总增加量, 因此R 代表一个生成或消灭的函数, 质量不减定律告诉我们:
∫x x+Δx[n(s, t+Δt) − n(s, t)]ds = [Q(x, t)−Q(x+Δx, t)]Δt
+∫x x+Δx (R(s, t )Δt) ds
两边除以ΔtΔx 后再令Δt → 0, Δx → 0我们得∂n/∂t = −∂Q/∂x + R 现在我们想想看Q这个函数与n 和φ的关系是什么, 考虑Q = Dn∂n/∂x +μnuE (其中E = −∂/∂x ), 这里Dn代表电子在硅晶格上的扩散系数(正数),Q 与∂n/∂x成正比, 意思是如果∂n/∂x= 0 即在x 点附近电子数相同, 即无扩散现象否则电子会往较稀疏的地方疏散, 另一项μnnE 其中μn 表示电子在组件内移动的能力(Mobility), 可以想象得到的是如果μn, n, 或E愈大, 则电子数量在时间t 通过x 点会愈大,因此μnnE 代表了Drift Diffusion Model中Drift 的意义, 而Dn =∂n/∂x表示Diffusion。以上的解释对电洞也成立, 因此有第(3) 式。
我们在这里省略了很多的物理参数, 条件, 变量等, 没有交待, 但是对于方程式(1)~(3) 的主要数学符号与相对应的物理意义希望已经提供了轮廓性的描述, 简单的说(1)~(3) 是一群电子在图三中从Source 跑到Drain 的数学表示式且仅适用于某些组件尺寸大小。
05、目前由半导体数学建构而成的模拟工具
基于上节各种不同的数学模式(Models), 全球有许多大学、相关研究机构, 甚至如英特尔、IBM 等公司皆有研究群全力地发展完整的半导体数值仿真器, 而功能较完整,且技术较先进的学术研究群有:
1、史丹福大学– TCAD 研究群。
2、麻省理工学院微系统科技实验室。
3、维也纳大学– TCAD 研究群。
4、普渡大学– 计算电子研究群。
5、美国计算电子研究中心。
其中, 史丹福大学的TCAD 研发团队,结合了电子工程、物理、数学、计算器等不同领域的人才、系所环境, 目前其技术领先世界水平约10年, 其相关的研究从制程仿真、组件仿真、电路仿真到系统都做, 也写计算数学核心。它所研发的SUPREM 和PISES两套仿真器, 由于功能强大, 广为商业界所爱用。
由威尼斯大学TCAD 团队所发展的MINIMOS Simulation Tool, 是早期几个少数仿真器中,功能更为完备, 更为成熟的仿真器, 举凡制程仿真, 组件仿真, 电路仿真都有做, 广为学术界所爱用。
而普渡大学的Computational Electronics Hub 是以TCAD 整合为主, 它搜集了所有可以见的到的TCAD 相关资料, 并以因特网浏览接口开放给学术界免费使用。
目前半导体工业界里, 有许多公司投入TCAD 的研发, 较著名的有: Silvaco、Integrated SystemsEngineering(ISE)、和Avant!, Silvaco 与Avant! 两公司的主要技术核心源自于史丹福大学TCAD 研究群所开发出来的学术性软件, 而ISE 的技术则源自于瑞士联邦科技大学以及维也纳大学。目前所知的所有组件仿真软件对于小于0.1微米的组件都无法获得满意的数值计算结果, 我们也正朝这些困难迈进, 希望能在此竞争非常激烈、时效性非常紧迫的研究领域有所突破与贡献。
06、结语
虽然半导体工业是目前我国最重要的工业之一, 但是十之八九的半导体制造商甚至学术研究实验室仍然以实验方式来取得所谓的what is done to it and how to control current,这样做有三个很大的缺点:
1. 成本过高、费时费工。
2. 无法取得较佳设计篮图与制造参数值
3. 容易造成污染。
这是整个半导体工业里很大的问题, 只要在半导体工业里带入所谓的半导体数学与软件, 将有助于解决上述问题; 而且当半导体组件的尺寸越小, 半导体工业就愈需要这些相关的基础研究了。
在半导体组件日渐缩小的情况下, 以前所被简略的物理特性也都一一呈现出其重要性来, 因此我们需要更为较精确更为复杂的数学模式来替代物理实验, 其所代表的意义是在更小的区域中未知函数的变化更为复杂,想要求得较精确的近似解则需要更多的计算量,进而使得仿真组件特性须要耗费更多的时间,另外, 数值模拟结果必需与实验相互验证、比较, 因此数学、物理与工程等领域的整合也是非常重要的环结, 所以半导体模拟是需要非常高度的科学计算技术与扎实的基础科学基础。
声明:本文版权归原作者所有,文章收集于网络,为传播信息而发,如有侵权,请联系小编及时处理,谢谢!
文章来源:数哲三叁叔
《视觉的盛宴:深度玩转人脸识别》作为高端课程,内容安排上也不同于传统的在线课程,本课程将分为经典算法实现(课内)和工程开发实践(课外)两个部分,覆盖五大核心问题,逐步引导学员,分级探索工程应用,鼓励和组织学员尝试产品设计,并可为优秀学员提供实习和创业机会。点击下方二维码报名课程: