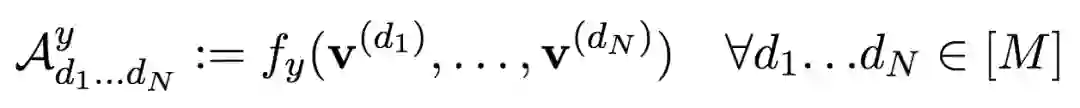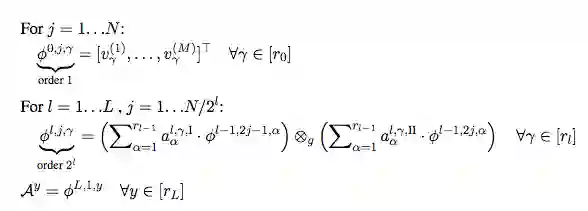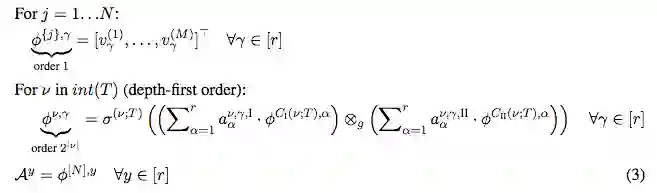基于混合张量分解提升扩张卷积网络
希伯来大学的研究人员Nadav Cohen、Ronen Tamari、Amnon Shashua将在ICLR 2018上口头报告他们的研究《Boosting Dilated Convolutional Networks with Mixed Tensor Decompositions》(基于混合张量分解提升扩张卷积网络)。该研究引入了混合张量分解这一新概念,证明了相互连通的扩张卷积网络提升了表达效率。该研究也是ICLR 2018十佳论文。
介绍
深度学习之所以如此成功,其中关键的推动因素之一就是深度神经网络能紧凑地表示多种多样的函数。近些年来,机器学习理论社区比较关注这一现象。社区提出了表达效率(expressive efficiency)的概念,以形式化地论证不同模型的表示能力。
表达效率的形式化定义为:给定网络架构A和B,其尺寸参数(通常为网络层的宽度)分别为rA、rB,当满足以下两个条件时,架构A的表达效率高于架构B:
任何由尺寸为rB的B网络实现的函数可以被A网络实现(或逼近),且rA ∈ O(rB)。
存在由尺寸为rA的A网络实现的函数,B网络无法实现(或逼近),除非rB ∈ Ω(f(rA)),f为超线性(super-linear)函数。 研究深度神经网络表达效率的研究,主要关注架构的深度,和较浅的网络相比,较深的网络表达效率更高。
然而,网络的连通性是否影响模型的表达效率,之前一直悬而未决。本研究通过连通扩张卷积网络(dilated convolutional network),得到了混合扩张卷积网络(mixed dilated convolutional network),并引入了相应的混合张量分解的概念,从而基于张量分析(tensor analysis)论证了连通性能够提升表达效率。
张量分析
让我们温习一下张量分析。
张量分析的核心概念是张量(tensor)。简单来说,张量就是多维数组(multi-dimensional array)。
下面举例说明有关张量的一些术语。
一个4 x 3的矩阵(matrix)是一个2阶(order)张量,2阶意味着它有2个模(mode),模1有4维(dimension),模2有3维(dimension)。
张量分析的基本运算是张量积(tensor product),记为⊗。替换张量积中的乘法运算,Cohen和Shashua在2016年提出了广义张量积(generalized tensor product),记为⊗g。
另外,σ(A)表示据σ函数对张量A进行模排列(mode permutation)后所得的张量。
研究张量时,常常需要将张量转化为二维数据,这一过程称为矩阵化(matricization)。
混合张量分解
最近,深度学习社区越来越关注扩张卷积网络。大多数传统的卷积架构主要应用于图像和视频,包含多个连续卷积层的扩张卷积网络则更多地应用于序列处理任务。例如,当前在音频和文本处理任务中达到最先进表现的WaveNet和ByteNet,就采用了扩张卷积网络。
研究人员基于张量分析研究了WaveNet所采用的扩张卷积网络(称为基线网络)。研究人员对网络的输入输出映射进行了离散化(discretization)处理。基线网络可以看成一个函数fy(x[t-N+1], ..., x[t]),其中t为自然时间索引。基于有限(指数级)的输入点,可以生成对应该函数的N维查询表。该查询表称为网格张量(grid tensor)。
该网格张量可以用层级张量分解(hierarchical tensor decomposition)表达:
这一表达称为基线分解(baseline decomposition)。
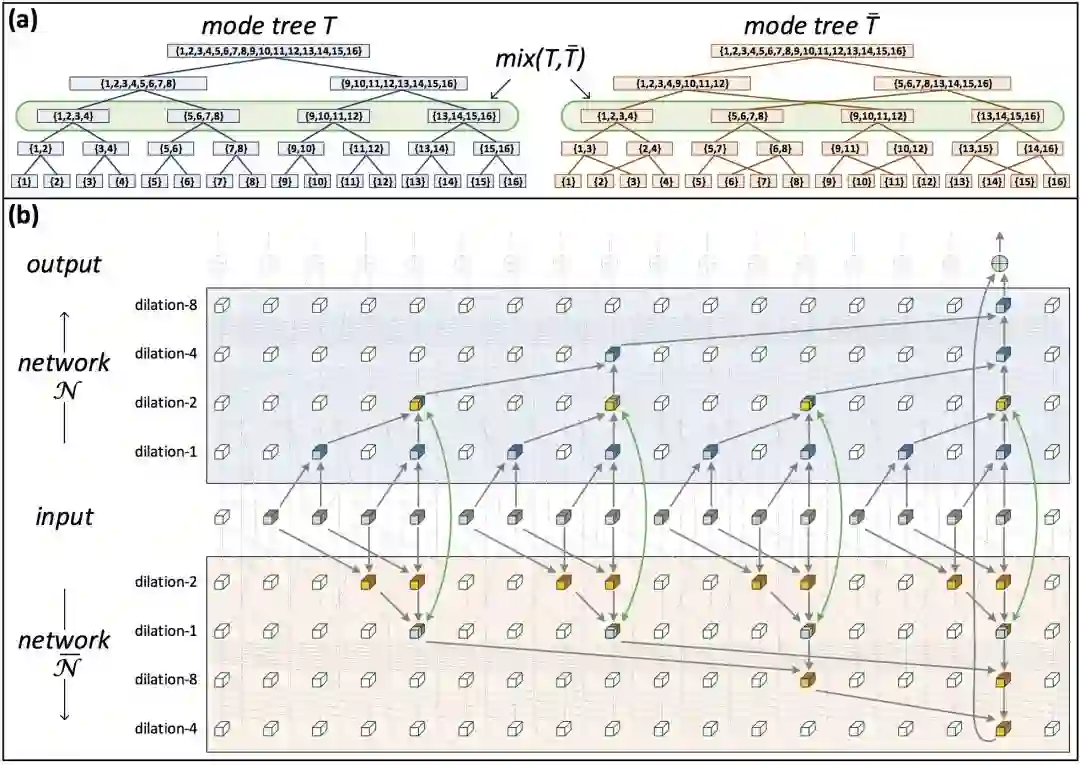
接着,研究人员引入了模树的概念,基于模树的层级张量分解表达,称为树分解(tree decomposition):
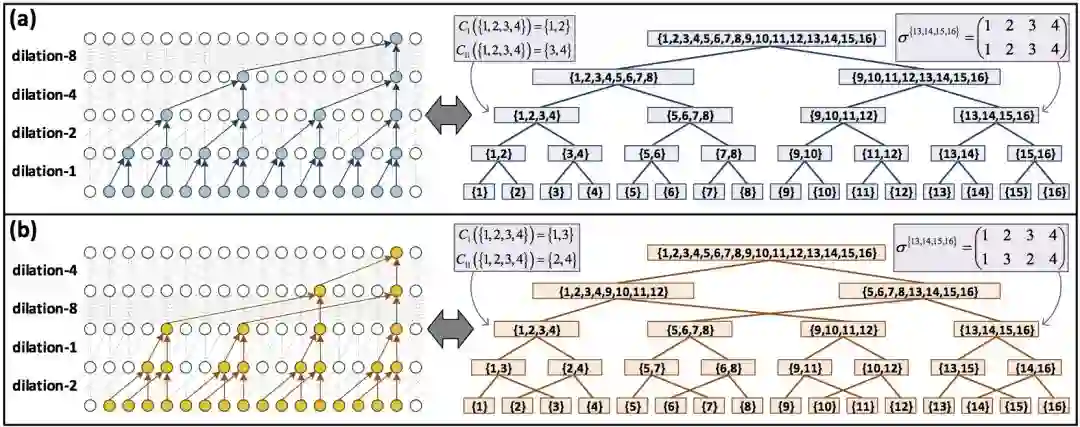
模树选择的不同导向不同的树分解,不同的树分解对应网络不同的扩张。研究人员关注的是基线网络和交换不同层的扩张得到的网络分别对应的树。
基于将不同的扩张卷积网络表示为对应不同的模树的层级张量分解的框架,研究人员引入了混合张量分解(mixed tensor decomposition)这一概念。
例如,上图右侧的两棵树,从中选取同时存在于两棵树的节点,称为混合节点(mixture node)。在每个混合节点处,交换两个分解的张量。将经混合张量分解后的两棵树对应的网络混合(互相连通),可以得到一个混合网络。
张量分解的形式化定义为:
然后,研究人员研究了混合网络相对于单独网络的表达效率。也就是说,任何由单独网络实现的函数可以由混合网络在尺寸不超过线性增长的前提下实现,相反,存在由混合网络实现的函数,无法被单独网络实现,或者实现的成本很昂贵(超线性的尺寸增长)。从张量分解的角度,这可以表述为两个命题:
混合分解可以在尺寸不超过线性增长的前提下,实现单个树分解。
存在混合分解可实现的张量,无法由单独树分解实现,除非允许超线性的尺寸增长。
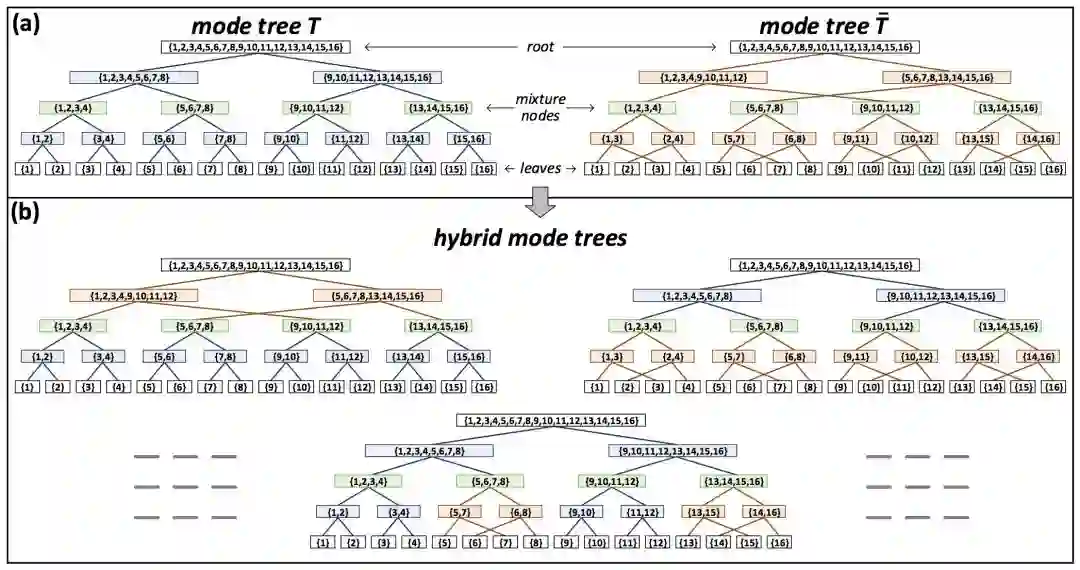
研究人员引入了混合模树(hybrid mode tree)的概念,通过组合两颗树,可得到混合模树。
上面的示意图展示了2棵模树的3种可能的混合模树。每棵混合模树是原模树的区间(segment)的组合。区间为特定根节点或混合节点的所有非叶子孙(non-leaf descendant),其中不通过其他任何混合节点。
研究人员证明了,2棵树的混合分解可以在尺寸不超过线性增长的前提下,实现任何混合树的树分解。由于单棵树是其本身的混合树,研究人员也就证明了上文的命题1。
接着,研究人员展示了,存在一个混合树的树分解只能通过超线性增长的树实现的情形,从而证明了上文的命题2。
篇幅所限,我们这里不给出具体的证明过程,不过可以简单讨论一下背后的直觉。
如前所述,混合张量分解在融合不同模树的树分解的过程中,交换了混合节点处的张量。我们可以把每个混合节点看成一个决策点,可以传播两个计算中的一个(由原本的两棵模树中的一棵承担的计算),无论传播的是哪一个计算,选定的计算都会同时在两棵模树间传播。所有混合节点处的决策组合产生了一个流经两棵树的计算路径,等价于混合模树的树分解。可能的混合模树的数量与混合节点的数量是指数关系,因此混合分解相当于指数级数量的混合模树的树分解(其中包括原本的树分解)。所以,混合分解当然可以表达原本的树分解能够表达的函数。另一方面,混合分解所代表的很多混合模树和原树差异显著,因此,混合分解能表达的函数,原本的树分解未必能表达,或者表达的代价会很昂贵。
试验结果
研究人员简单测试了混合扩张卷积网络的表现。
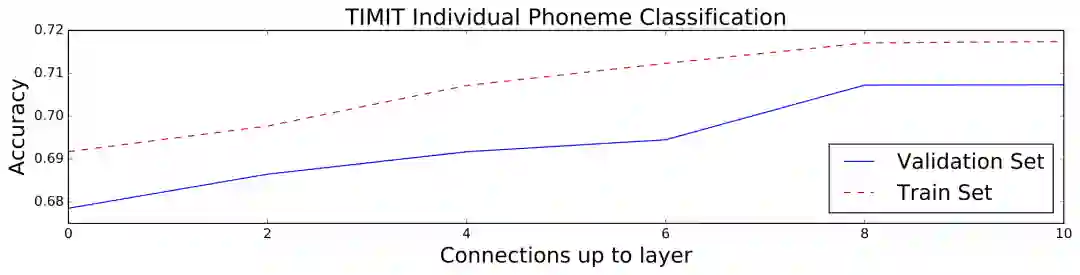
研究人员在TIMIT语音语料库上训练了基线扩张网络(使用和WaveNet类似的架构参数),交换基线网络的奇数层和偶数层的扩张所得网络,以及一些基于两者的混合扩张网络。下图显示了训练效果,当网络间的连通性增加时,在不增加额外的算力成本的前提下,分类精确度也增加了。
TIMIT数据集包含6300句人工标注音位的语音。
如前所述,基线网络使用与WaveNet类似的配置:
ReLU激活(g(a, b) = max{a+b, 0})
每层32通道
用256维one-hot输入向量表示音频信号
12层网络,输入窗口为
2 ** 12 = 4096样本
研究人员基于Caffe框架搭建了网络,使用Adam优化(默认超参数,β1 = 0.9、β2 = 0.999,学习率 0.001),相应的权重衰减和batch尺寸为10-5、128。训练迭代数为35000。
论文地址
论文可通过预印本文库获取: arXiv:1703.06846