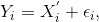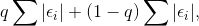数据分析师应该知道的16种回归技术：分位数回归

2018 年 8 月 8 日 数萃大数据

分位数回归是线性回归的扩展，当数据中存在异常值或数据具有高偏性和异方差性时，可以采用分位数回归来分析数据。

线性回归是给定的自变量，预测因变量的均值。由于均值不能描述整个分布的属性，因此对均值的建模不能充分反映自变量与因变量间的相互关系。分位数会回归可以基于给定的自变量预测因变量的任意分位数或百分比。对于分位数回归，需要注意的是它只适用于具有连续型因变量的数据集。

分位数回归

对于q分位数，设回归模型：

看上去像线性回归模型，但是最小化的目标函数为：

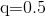
对应一种特殊的分位数回归模型：中位数回归或绝对最小偏差回归，此时对应的最小化目标函数为：

注：不同分位数下模型参数的估计值也不同。

同线性回归相比，分位数回归具有以下优势：

益于异方差数据分析
对异常值稳健
通过不同的分位数描述因变量的分布特征
当数据有偏时，比线性回归更有用

案例

R中进行分位数回归可以使用quantreg包中的rq函数，该函数的使用方法与lm函数相同，另外这个包也提供了关于分位数回归的可视化方法，如查看某个系数在不同分位数回归下的变化情况和置信区间。

构造具有异方差的变量

  
  
    
   
   
     x <- seq(0,100,length.out = 100)
   
   
     sig <- 0.1 + 0.05*x
   
   
     b_0 <- 6;b_1 <- 0.1
   
   
     set.seed(1)
   
   
     e <- rnorm(100,mean = 0, sd = sig)
   
   
     y <- b_0 + b_1*x + e 
   
   
     dat <- data.frame(x,y)

在不同分位数下进行分位数回归

  
  
    
   
   
     qs <- 1:9/10
   
   
     qr <- rq(y ~ x, data=dat, tau = qs)
   
   
     coef(qr)

线性回归

  
  
    
   
   
     lr <- lm(y ~ x, data=dat)
   
   
     coef(lr)

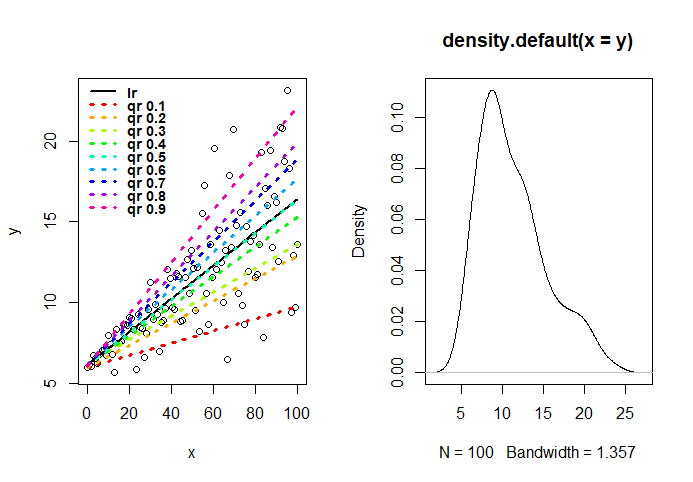
下面左图是y的密度图，可以看到y稍微左偏(不同教材关于左右偏的定义不同，这里认为那边胖尾朝那边偏)；右图是lr和qr拟合图，可以看到qr=0.5(中位数回归)的拟合曲线几乎和lr拟合曲线一致。

  
  
    
   
   
     op=par(mfrow=c(1,2))
   
   
     cols <- rainbow(9)
   
   
     plot(x,y)
   
   
     lines(x,coef(lr)[1]+x*coef(lr)[2],lwd=2)
   
   
     for (i in 1:9) {
   
   
       lines(x,coef(qr)[1,i]+x*coef(qr)[2,i],lty=3,
   
   
             col=cols[i],lwd=3)
   
   
     }
   
   
     legend('topleft',c('lr',paste('qr',qs)),
   
   
            lty=c(1,rep(3,9)),lwd = c(2,rep(3,9)),
   
   
            col = c('black',cols),bty = 'n',
   
   
            cex = 0.85,text.font = 2)
   
   
     plot(density(y))
   
   
     par(op)

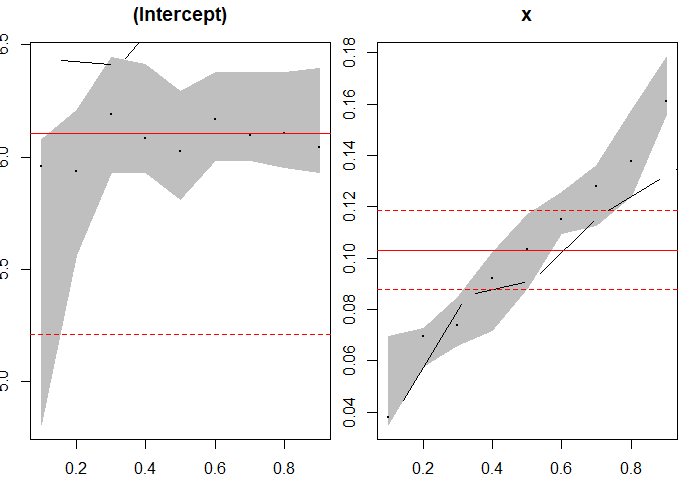
查看不同分位数下截距和斜率的变化，图中的红色实线是线性回归下的截距和斜率，红色虚线是其对应的95%区间.由于quantreg包对基础绘图中plot的改写,一页多图能使用par中mfrow和mfcol设置，不过cowplot中的plot_grid函数可以解决这个问题，它适用于一切绘图系统的一页多图设置。

  
  
    
   
   
     p1=function() plot(summary(qr),'(Intercept)')
   
   
     p2=function() plot(summary(qr),'x')
   
   
     cowplot::plot_grid(p1,p2)