人工智能数学基础【文末赠书】

2020 年 12 月 6 日 AINLP

数学是思维的体操，也是学习人工智能的基石。在人工智能算法的学习过程中，很多初学者遭遇的挫折多半是来自看不懂算法的数学推导过程，进而无法理解算法原理，在应用中只能调整参数或换工具包，却很难优化算法。要理解一个算法的内在逻辑，没有必要的数学知识是不行的，这一点是人工智能编程和以往传统程序编程的不同之处。

下面通过一些案例了解一下：

Python中常用的定积分求解方法及案例解析

【例1】应用SciPy科学计算库求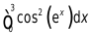的定积分。

解：本例题使用了SciPy科学计算库的quad函数，它的一般形式是scipy. integrate.quad(f,a,b)，其中f是要积分的函数名称，a和b分别是下限和上限。

【代码如下】

>>> import numpy as np

>>> from scipy.integrate import quad

>>> func=lambda x:np.cos(np.exp(x))**2 #定义被积分函数

>>> solution=quad(func,0,3) # 调用quad积分函数

>>> print （solution）

【结果说明】

输出结果：(1.296467785724373, 1.397797133112089e－09)。前一个为积分值，后一个为误差。

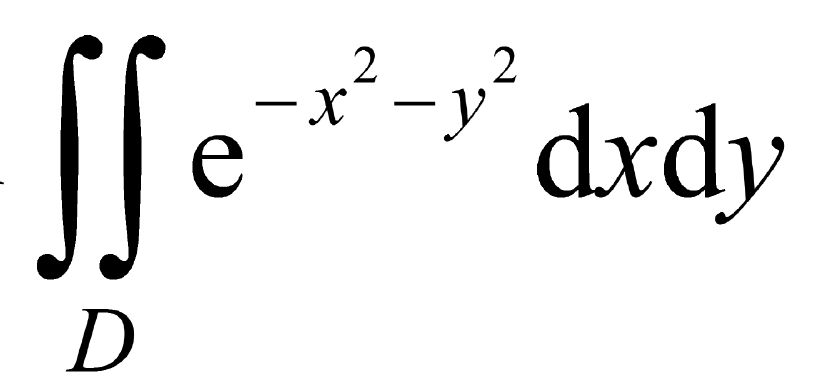
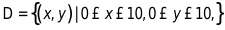
【例2】应用SciPy科学计算库求，其中。

解：dblquad函数的一般形式是scipy.integrate.dblquad(func,a,b,gfun,hfun)。其中，func是要积分的函数名称，a和b分别是变量x的下限和上限，gfun和hfun是定义变量y的下限和上限的函数名称。请注意，即使gfun和hfun是常数，它们在很多情况下也必须定义为函数。例如本题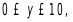，即使y的下限和上限为常数，也要定义函数为gfun(x)=0、hfun(x)=10。本题函数gfun(x)、hfun(x)的表达形式为lambda x:y_a 和lambda x:y_b，其中y_a 、y_b的值分别为0和10。

【代码如下】

>>> import numpy as np

>>> from scipy.integrate import dblquad

>>> def integrand(x,y):

... return np.exp(－x**2－y**2)

>>> x_a=0

>>> x_b=10

>>> y_a=0

>>> y_b=10

>>> solution,abserr=dblquad(integrand,x_a,x_b, lambda x :y_a,lambda x:y_b)

>>> print(solution,abserr)

【结果说明】

输出结果：(0.7853981633974476,1.375309851021853e－08)。第一个为积分值，第二个为误差。

以上采用SciPy科学计算库中的数值积分函数直接求解定积分，下面通过定积分定义的基本概念，编程模拟实现求解定积分。

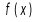
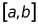
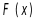
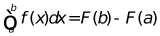
从上节内容知道，函数在区间上连续，且其原函数为，则可用牛顿－莱布尼茨公式求定积分的值。牛顿－莱布尼茨公式无论在理论上还是在解决实际问题上都具有重要作用，但它并不能完全解决定积分的计算问题，有些情况它就无能为力，例如，被积函数的原函数很难用初等函数表达出来、原函数存在但表达式太复杂、被积函数没有具体的解析表达式、函数关系由表格或图形表示等。这些情况中，积分并不十分准确。因此，利用原函数计算积分具有局限性。

根据3.3小节定积分的定义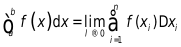可知，定积分的求解过程大致分为以下4个步骤。

（1）分割，。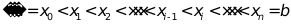

（2）近似，。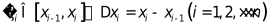

（3）求和，。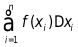

（4）求极限，。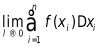

上面的求解过程为使用计算机求解定积分提供了算法思路。将求积区间进行n等分，步长为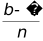，循环n次求解n个小梯形面积之和，结果即为定积分近似解。

【例3】应用Python编程实现求定积分近似解，并用例3.6进行验证。

解：数值计算是指有效利用计算机求数学问题近似解的方法与过程，以及由相关理论构成的学科。数值计算主要研究如何利用计算机更好地解决各种数学问题。本例求定积分近似解是数值计算研究领域的一个典型应用。

【代码如下】

>>> from numpy import *

>>> a,b=0,3

>>> def f(x): #例3.6的求积函数模型

... return cos(exp(x))**2

>>> def trape(n): #数值计算

... h=(b－a)/n

... x=a

... sum=0

... for i in range(1,n):

... x2=a+i*h

... sum=sum+(f(x)+f(x2))*h/2

... x=x2

... return sum

...

分别将求积区间进行n=10，100，1000，10000，100000等分，用来验证自定义的求定积分函数trape(n)的结果值。

【运行结果】

>>> trape(10)

0.944822326405313

>>> trape(100)

1.2843391540917448

>>> trape(1000)

1.2960750567338157

>>> trape(10000)

1.296434741500134

>>> trape(100000)

1.2964645400078032

【结果说明】

从结果可以看出，当积分区间分为100000等份时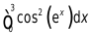，的值为1.2964645400078032，与例3.6的结果近似。本例求定积分的算法过程来源于最基本的定积分数学描述原理，并运用Python编程实现，经过实例验证，定积分求解结果达到要求。在本例中积分区间还可以继续细分，直到结果值基本不再变化时，可以达到更高的精确度。

本文摘自北京大学出版社《人工智能数学基础》一书。文章略有修改，请按照出版图书为准，经出版社授权发布。

最后，福利时间，这次我们还是直接抽奖，送4本《人工智能数学基础》，感兴趣的同学可以关注【Python时代与机器学习】，回复【读书】获取抽奖小程序直接参与抽奖即可，截止12月9日周三晚20点，感谢大家的关注：

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。