数学和物理的共同演化

2018 年 6 月 20 日 中科院物理所

本文经「原理」（微信公众号：principia1687）授权转载，

禁止二次转载。

物理领域的重大突破有时需要数学的协助，反之亦然。

1905年，爱因斯坦提出了狭义相对论，将时间和空间联姻，这使我们对宇宙的理解发生了革命性的变化。然而，狭义相对论的成功，并没有阻止他进一步地探索更深层的问题，因为他还没有将引力的影响纳入到他的理论中。

七年后，当时在苏黎世联邦理工学院的爱因斯坦，正酝酿着一个可以颠覆牛顿万有引力定律的理论。但是，爱因斯坦在扩展狭义相对论时却遇到了难题，他必须通过使用一些新的方法和技巧才有可能完成这一壮举。幸运的是，爱因斯坦的好朋友和同事格罗斯曼（Marcel Grossmann）伸出援手，带来了一个十分令人激动的优雅方法：黎曼几何。

○ 黎曼在19世纪发展出了一套特殊的曲率几何概念时，他丝毫没在意过物理学。那时的他绝对想不到，在20世纪初，他的工作会在爱因斯坦的笔下为物理学的革命性发展起到推波助澜的作用。| 图片来源：symmetrymagazine

十九世纪中叶，德国数学家黎曼（Bernhard Riemann）发展了黎曼几何的数学框架。在当时，黎曼几何本身就是一个具有革新性的框架。不同于之前将数学图形看成是三维空间的子集，黎曼几何通过更本质的方法直接研究图形的性质。例如，一个球可被看作是三维空间内所有距离原点刚好为1的点的集合。但它也可以被视为每一个点都有着特殊曲率属性的二维物体。后面的这种定义对于理解球这样的几何图形来说或许不是那么重要，但对于更复杂的流形和更高维的空间，这种定义的价值就显而易见了。

在1912年的时候，黎曼几何依然是一个新颖的理论，还未完全渗透到数学领域，但它正好是爱因斯坦所需要的。黎曼几何赋予爱因斯坦一个强大的数学基础，使他得以构建出一个全新的引力理论——广义相对论的准确等式。1913年，爱因斯坦和格罗斯曼发表了他们突破性的工作。理论物理学家 Peter Woit 认为“如果没有数学家的帮助，很难想象爱因斯坦怎样才能完成相对论的工作。”

广义相对论的故事当然能让数学家们感到骄傲。在这个故事里，数学仿佛就像是一个引路人，在恰当的时机出现在物理学家的身边，为一片灰暗的物理学世界带来光明。

但是，数学和物理的相互影响远比这个故事里讲述的更复杂。在大部分有记录的历史中，物理和数学甚至不是分开的学科。古希腊、埃及和巴比伦的数学认为我们生活在一个距离、时间和重力都按某种特定方式运行的世界中。

布朗大学的物理学家 Sylvester James Gates 说，“牛顿是第一个为了达到学术巅峰而发明一项新的数学领域的物理学家。这个数学领域就是微积分。”

微积分让解决一些经典的几何问题变得更加简单，但其最初的目的是为牛顿提供了一种分析运动的新方法，以及改变了牛顿观察物理的视角。在这个关于微积分的故事中，数学更像是一个让一切事物变得井然有序的管家，而不是在危难关头力挽狂澜的救世主。

即使物理和数学成为了两个学科之后，他们之间仍然是紧密联系的。“回溯物理和数学的早期发展历程，你会发现确定一个人是物理学家还是数学家是很困难的。” Woit说道。

○ 诺特（Emmy Noether）将自然界中的对称性和守恒定律联系了起来，可以说她是史上最具深刻洞见的数学物理学家之一。对于一些数学家而言，看到诺特的名字出现在物理学领域是令人惊讶的，因为他们多数是通过抽象代数才了解她的。| 图片来源：symmetrymagazine

纵观历史，数学和物理这两个领域都给对方提供过重要的概念。数学家外尔（Hermann Weyl）在李群（Lie group）方面的工作就为理解量子力学中的对称性提供了非常重要的基础。理论物理学家狄拉克在他1930年的著名书籍《量子力学原理》中，就使用了狄拉克道尔塔(δ)函数来描述粒子物理中点粒子的概念（点粒子描述的是任何小到可以用一个点来模拟的理想化情况）。二维的δ函数在x=0的位置的值为无穷大，而在其他任何地方都为0。狄拉克声明δ函数的积分、也就是δ函数所覆盖的面积为1。严格地讲，并不存在具有这种性质的函数。但是狄拉克对δ函数的使用最终启发了数学家施瓦茨（Laurent Schwartz），他用严密的数学方式发展出了分布理论。现如今，分布理论在常微分方程和偏微分方程领域已经变得极为重要。

尽管现代研究人员对自身领域的关注越来越多，研究领域的细化和专业化也越来越明显，但物理和数学的界限仍然模糊。一个物理学家可以获得数学领域最具权威的奖项之一——菲尔兹奖。而一个数学家，比如Maxim Kontsevich，也可同时获得科学突破奖的物理奖和数学奖。现在，人们可以参加由数学系或者物理系举办的关于量子场论、黑洞或者弦论的研讨会。自2011年起，弦数学（String Math）的年度讨论会议就把数学家和物理学家汇聚到了一起，让他们一同研究弦论和量子场论中的交叉领域。

弦论可能是关于数学和物理互相影响的最佳示例。在弦论的理论框架中，狄拉克所描述的点粒子变成了一维的弦。这个理论模型中的一部分描述了一种被称为引力子的理论粒子，这是一种传递引力的假想粒子。

大多数人认为我们通过三维的空间和一维的时间来感知宇宙。但是弦论却是构架在十维中的。在1984年，随着研究弦论的物理学家激增，包括后来被授予菲尔兹勋章的物理学家威滕（Edward Witten）在内的一批研究人员发现了弦论所需空间中的另外六个维度，被称为卡拉比-丘流形（Calabi-Yau manifold）。

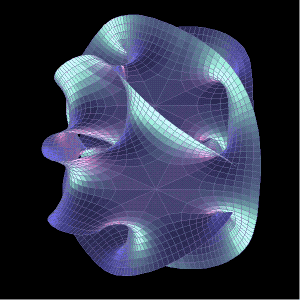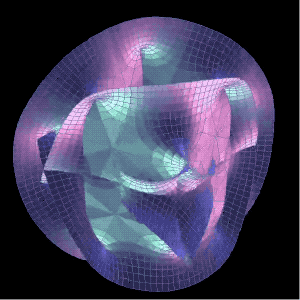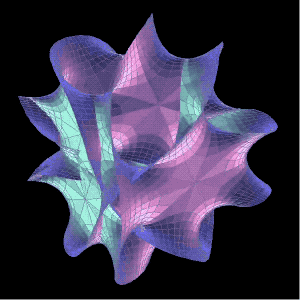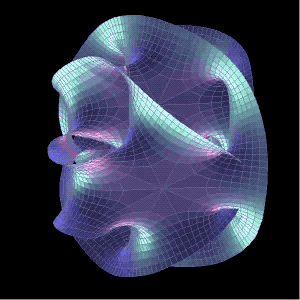
○ 六维卡拉比-丘流形。| 图片来源：Jeff Bryant / Visualization

当数学家们还在为阐明各种流形的结构而争吵时，物理学家只希望能获得几个可能有效的数学结果，他们找到了卡拉比-丘流形。而数学家却还不能确定他们对流形的划分是正确的。

当物理学家和数学家研究这些空间结构的时候，他们发现卡拉比-丘流形具有非常有趣的对偶性。两个看起来完全不同的流形可能描述的是同一种物理结构。这背后的思想被称为镜像对称。这种性质的研究在数学中迅速繁荣，并形成了一个全新的数学分支。弦论的框架几乎成为了数学家的游乐场，带来了无数新的研究分支。