NeurIPS 2021 | 寻找用于变分布泛化的隐式因果因子

论文链接:
https://arxiv.org/pdf/2011.02203
代码链接:
https://github.com/wubotong/LaCIM
这篇论文将 CSG 模型推广到了多训练域的情况,即用来处理领域泛化(domain generalization)任务,并给出了相应的算法和理论。为了建模与领域标号 d 的关系,此时的先验分布记为 p^d (s,v)。为避免在图模型中以及在算法和理论中暗含给定 d 之后 s 与 v 的独立性,研究员们引入了混淆变量(confounder)c。它解释了 s 与 v 之间的虚假关联(spurious correlation),因为尽管 s 和 v 之间没有因果关系,但若忽略 c,那看上去 s 和 v 就会有相关性:p^d (s,v)=∫p^d (c) p^d (s│c) p^d (v│c) dc。拓展后的模型如图5所示,被称为隐式因果不变模型(Latent Causal Invariant Model,LaCIM)。
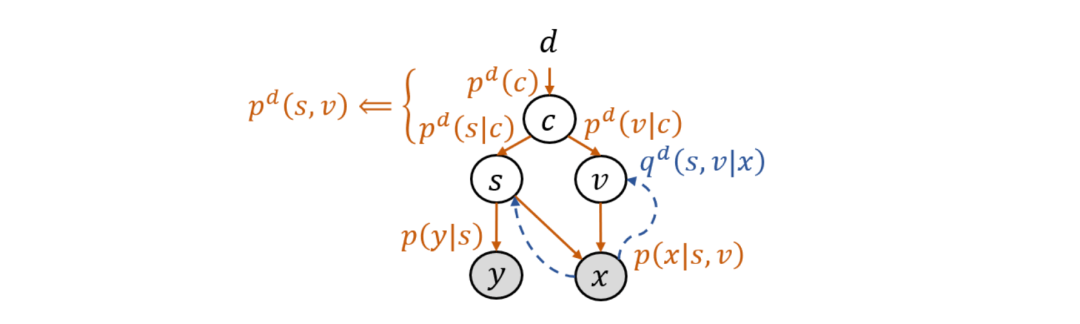
图5:隐式因果不变模型(LaCIM)
LaCIM 的训练方法与 CSG 类似,只是需要对所有训练域上的目标函数求和,并在各训练域上使用各自的先验模型 p^d (s,v) 和推断模型 q^d (s,v│x)。而其预测方法则与 CSG-ind 类似,区别在于推断 (s,v) 不通过一个推断模型,而是直接使用最大后验估计(maximum a posteriori estimate, MAP):p^(d^' ) (y│x)=p(y│s(x) ), 其中 (s(x),v(x))≔argmax_(s,v) p(x│s,v) p^⊥ (s,v)^λ .
理论
由于需要建模各分布与领域标号 d 的关系,理论分析中需要加入更多的结构。因此,假设 c∈[C]≔{1,…,C},且 p^d (s│c) 和 p^d (v│c) 都属于指数分布族(exponential family),进而定义相应的识别性概念,称为指数识别性:存在一个可从真实 LaCIM 变换到所学 LaCIM 的重参,且此重参可在允许一个分量置换和整体平移的意义下分别恢复出真实 p^d (s│c) 和 p^d (v│c) 的充分统计量。
定理(多训练域上的指数可识别性):假设 p(x│s,v) 和 p(y│s) 是特定加性噪声形式,且 p^d (s│c) 和 p^d (v│c) 的充分统计量线性独立。那么当各训练域在特定意义下足够多样时,一个学好了的 LaCIM 就取得了指数识别性。
此定理的结论(取得指数识别性)比单训练域上可识别性定理的结论(取得语义识别性)更强。这体现在,前者不仅要求后者所要求的学到的 s 未混入真实的 v,还要求学到的 v 未混入真实的 s,即要求学到的 s 和 v 是解耦的(disentangled)。之所以能得到更强的结论,是因为多个足够多样的训练域为模型带来了更多的信息,且指数分布族也为模型带来了更具体的结构。另外,此结论也强于 identifiable-VAE [Khemakhem’20] 的结论,因为此结论要求充分统计量的分量置换不能跨越 s 和 v 的内部。
实验
在实验中,研究员们选择了一些最新的领域泛化数据集,包括 NICO 自然图片数据集、彩色 MNIST,以及预测阿尔兹海默症的 ADNI 数据集。表2中的结果表明 LaCIM 取得了最好的表现。可以注意到 LaCIM 也比不区分 s 和 v 的变种 LaCIMz 表现好,说明了将 s 和 v 分别建模的好处。图6中的可视化分析表明,LaCIM 很好地区分开了语义和多样因子,且关注图片中具有语义信息的区域。
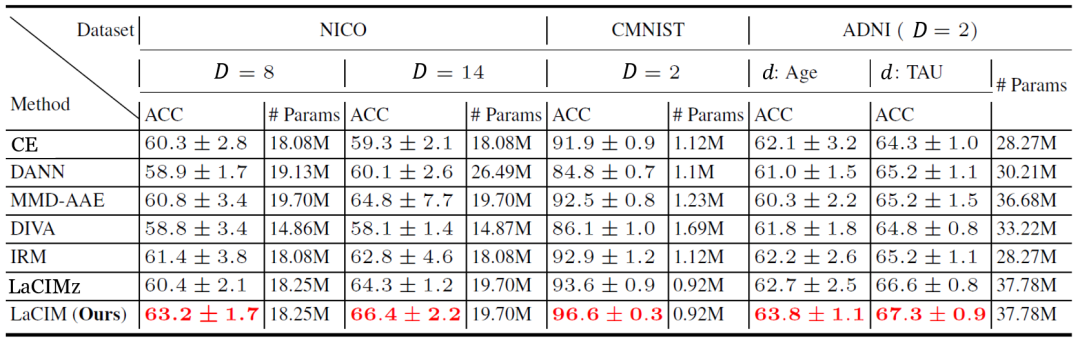
表2: 领域泛化的各数据集上各方法的表现(预测准确度%)

图6:领域泛化任务中各方法的可视化结果
专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)
后台回复“LCFG” 就可以获取《NeurIPS 2021 | 寻找用于变分布泛化的隐式因果因子》专知下载链接





