学界 | 用单张图片推理场景结构：UC Berkeley提出3D景深联合学习方法

选自BAIR Blog

作者：Shubham Tulsiani、Tinghui Zhou

机器之心经授权编译

参与：smith、蒋思源、李泽南

最近，UC Berkeley 的研究人员撰文介绍了他们在计算机视觉研究中的最新成果：利用单幅图片进行 3D 推断的计算模型。据介绍，新的方法可以在未经有标记数据训练的情况下达成很好的表现。这种方法在无人驾驶汽车等领域具有很大潜力，同时，研究人员认为构建新模型的原则也可以应用到机器学习的其他领域中。目前，该研究相关的两篇论文已经提交 CVPR2017 大会。

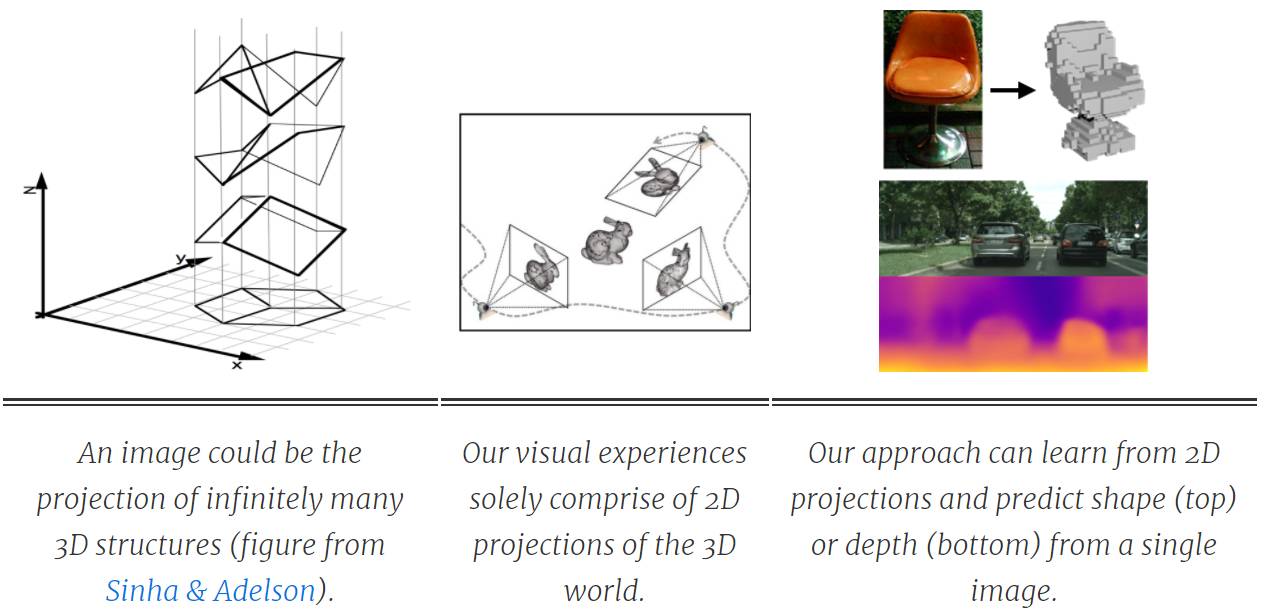
给定一张平面图，人类很容易推断出潜在场景丰富的三维结构。因为从平面图推断立体结构是一种模糊性的任务（如下图左边），我们必须依赖过去的视觉经验。这些视觉经验都是从三维世界在二维上的投影（视网膜上的投影）而获得的。因此，我们的三维感知能力的学习信号可能就来源自在世界不同的角度间建立起一致性联系，从而获取三维真实世界的信息。UC Berkeley 的研究人员提出了一种类人的方法，该方法可以构建三维场景的预测系统。

构建单幅图片 3D 推断的计算模型一直是计算机直觉中探讨的问题。早期的 Blocks World（论文：Machine perception of three-dimensional solids）或 3D surface from line drawings（论文：Interpreting Line Drawings as Three-Dimensional Surfaces）等项目都是利用几何线索的显式推理来优化三维结构。近年来，利用监督学习方法可以获得更加真实的设定和三维表征的定性推断（Hoiem et al.）或定量推断（Saxena et al）。在真实设定中获得优秀成果的趋势已经随着目前基于 CNN 实体（e.g. Eigen & Fergus, Wang et al.）的发展而进步，但它是以增加直接 3D 监督为代价的，所以这种范式相当有限。获得这种大规模监督数据的成本是巨大的，因此我们希望我们的计算系统能像人一样不需要 3D 监督而学习进行 3D 预测。

考虑到这一目标，我们的研究工作和其他最近的方法都在探索另外一种形式的监督：为学习单视角的三维结构而建的多视角观察（multi-view observations）。有趣的是，这些不同的研究工作不仅分享了合并多视角监督这一目标，同时应用的方法都遵循共同的原则。这些方法的统一基础是学习和几何之间的相互作用，学习系统所进行的预测期望和多视角观察得到「几何一致性（geometrically consistent）」。因此，几何学就成为了学习系统和多视角训练数据间的桥梁。

通过几何一致性（Geometric Consistency）进行学习

我们的目的是去学习一个预测器 P（通常是一个神经网络），它可以根据单幅 2D 图像推断出 3D 结果。在监督环境下，训练数据包含不同视角的多种观测结果。就像之前提示的那样，几何图形就像一个桥梁，它使用训练数据来学习预测器 P。这是由于我们清楚地知道在简明的几何方程的形式下，3D 表征和对应的 2D 投影之间的关系。因此我们就可以通过训练 P 来预测 3D 结果，此 3D 表征和与其相关联的 2D 观察结果是保持几何一致性的。

为了说明训练过程，在预测器 P 和几何输出之间设置了一个简单的策略网络，检验器 V。我们给 P 输入一个单一的图像 I，而且它预测出了一个 3D 形状 S. V，然后此 3D 形状 S. V 会被给予预测结果 S，和一个来此不同相机视角 C 的观测结果 O，它会使用几何方程来验证这些结果是否是一致的。我们让 P 去预测 S，从而能通过 V 的一致性检测。其中的核心就是由于 P 不知道（O，C）将要用来验证其预测结果，它将不得不去预测与所有可能观察结果相一致的 S（与未知的真实值 Sgt 相似）。这就使我们要定义下面的训练算法，从而在仅使用多视角监督（multi-view supervision）的情况下来学习从 2D 到 3D 的预测结果。

• 选取一个随机训练图像 I，此图像与从视角 C 观察到的结果 O 相关。

• 预测 S=P(I)。使用 V 来检测（S,O,C）的一致性。

• 更新 P，使用梯度下降，使 S 与（O，C）更一致。

• 重复此过程直至其收敛。

近期使用多视角监督来推行单一视角预测的方法全部遵守此模板，差异就是被推行的 3D 预测形式（例如深度或形状），和所需多视角观察结果的种类（例如彩色图像或者前景模板）。我们现在正在关注的两篇论文可以推进多视角监督模型的发展。第一篇论文利用经典射线一致性公式引入了一个一般的检验器，可以测量 3D 形状与不同种类观测结果 O 间的一致性；而第二篇论文说明了进一步解放所需要的监督是具有可能性的，并且提出了一个方法来学习从 2D 到 3D 的预测结果，它甚至没有利用训练时所需的相机视角 C。

可微分射线一致性（Differentiable Ray Consistency）

在我们近期的论文中，我们制定了一个检验器 V 来测量 3D 形状（表现为一个概率占据网格）和 2D 观察结果间的一致性。我们的通用性公式通过利用不同种类的多视角观察结果来对体积式的 3D 预测结果进行学习，比如监测到的前景模板，深度，彩色图像，语义等。定义 V 是因为观察结果 O 中的每一个像素都对应一条有相关信息的射线。然后我们可以想象一下，一次一条射线，计算形状 S 和射线 r 之间的一致性，这样就不用计算观察结果 O 和形状 S 之间的几何一致性了。

上图描绘了形式化射线一致性的各方面成本。a) 我们测量一致性的三维形体预测和样本射线。b,c) 我们通过三维形体和计算事件概率追踪射线，即不同路径上射线最终投影点的概率。d) 我们可以度量射线终止事件和该射线可用信息之间的不一致性成本。e) 通过间射线一致性成本定义为时间成本期望值，我们可以计算梯度以更新为更具一致性的预测。在这个案例中，我们可视化了一个深度观察 O，我们方法的优势在于它可以通过简单定义相应的事件成本函数而允许合并多种观察（如颜色图片、前景等）。

使用我们的框架在不同设定中从二维预测三维的结果展示在下图。注意，所有的可视化预测都是从预测器 P 训练的单张 RGB 图像中获得，并且没有使用 3D 监督。

在未监督视频中学习深度和视角

请注意，在上述工作中，输入验证器 V 的内容是已知摄像头视角的。这从具有感觉运动功能的智能代理（例如具有里程记录设备的人或机器人）的角度来看是合理的，但在应用到更多非结构化数据源（例如视频）时会面临挑战。在另一篇近期发表的论文《Unsupervised Learning of Depth and Ego-Motion from Video》中，研究人员展示了姿态要求也是不必要的，事实上我们可以使用单张图片联合学习进行 3D 预测。

更具体地说，验证器 V 在这个例子中是基于可微分的深度视角合成器在源视角（即观察者视角）的基础上通过预测深度和像素输出的目标视角。在这里深度建图和摄像头视角都被预测，随后通过合成的和实际目标视图之间的像素重建误差来定义一致性。通过联合学习场景几何和摄像头姿态，我们能够对未经标记的视频剪辑进行系统训练，无需任何有关深度或视角的直接监督。

让验证器形成深度视图合成器，同时学习深度和图像角度，可以让我们在图像未经直接监督标记深度和角度的情况下训练整个系统。

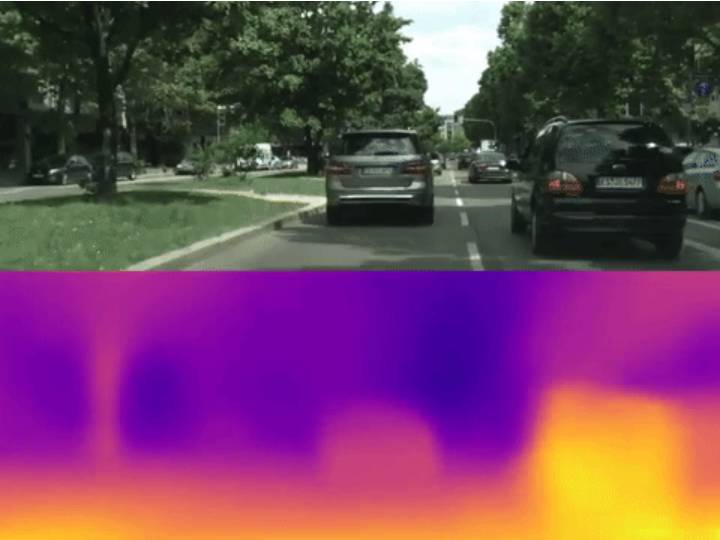
研究人员在 KITTI 和 Cityscapes 数据集中训练并评估了新系统的性能，其中包括汽车在市内行驶时驾驶员视角的视频片段。下图展示了我们的单视角深度网络逐帧（即时且平滑）预测的能力。

更多细节可以在项目页面找到：https://people.eecs.berkeley.edu/~tinghuiz/projects/SfMLearner/

令人惊讶的是，尽管未经任何真值标签的训练，我们的单视角深度模型已经与一些基线监督模型达到同样的效果了，而姿态估算模型也与建立完备的 SLAM 系统相当。

在最近发表的论文《Unsupervised Learning of Depth and Ego-Motion from Video》中，你可以找到其中的更多细节：https://arxiv.org/abs/1704.07813

在计算机视觉领域里，学习单图 3D 场景而不经过 3D 监督是一个激动人心的课题。使用几何作为学习系统和多视角训练数据的桥梁可以让我们绕过获取地面真值 3D 标签繁琐而昂贵的过程。更广泛的说，人们可以将几何一致性解释为元监督的一种形式，不推测眼前的事物是什么，而去推测它的行为是什么样的。UC Berkeley 的研究者们相信这种原则可以应用到其他领域中去，在训练数据缺乏标记的情况下让机器学习发挥作用。

感谢 Alexei Efros 与 Jitendra Malik 对本研究的悉心指导。

本文基于以下两篇论文（均已被 CVPR 2017 大会接收）：

Multi-view Supervision for Single-view Reconstruction

via Differentiable Ray Consistency. S. Tulsiani, T. Zhou, A. A. Efros, J. Malik. In CVPR, 2017：https://shubhtuls.github.io/drc/

Unsupervised Learning of Depth and Ego-Motion from Video. T. Zhou, M. Brown, N. Snavely, D. Lowe. In CVPR, 2017：https://people.eecs.berkeley.edu/~tinghuiz/projects/SfMLearner/

近期其他多视角 3D 监督预测方法的研究：

Unsupervised CNN for Single View Depth Estimation: Geometry to the Rescue. R. Garg, B. G. Vijay Kumar, G. Carneiro, I. Reid. In ECCV, 2016：https://arxiv.org/abs/1603.04992

Perspective Transformer Nets: Learning Single-View 3D Object Reconstruction without 3D Supervision. X. Yan, J. Yang, E. Yumer, Y. Guo, H. Lee. In NIPS, 2016：https://sites.google.com/site/skywalkeryxc/perspective_transformer_nets

Unsupervised Learning of 3D Structure from Images. D. J. Rezende, S. M. Ali Eslami, S. Mohamed, P. Battaglia, M. Jaderberg, N. Heess. In NIPS, 2016：https://arxiv.org/abs/1607.00662

3D Shape Induction from 2D Views of Multiple Objects. M. Gadelha, S. Maji, R. Wang. arXiv preprint, 2016：http://mgadelha.me/home/prgan/index.html

Unsupervised Monocular Depth Estimation

with Left-Right Consistency. C. Godard, O. M. Aodha, G. J. Brostow. In CVPR, 2017：http://visual.cs.ucl.ac.uk/pubs/monoDepth/

原文链接：http://bair.berkeley.edu/blog/2017/07/11/confluence-of-geometry-and-learning/

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者/实习生）：hr@jiqizhixin.com

投稿或寻求报道：editor@jiqizhixin.com

广告&商务合作：bd@jiqizhixin.com

点击阅读原文，查看机器之心官网↓↓↓