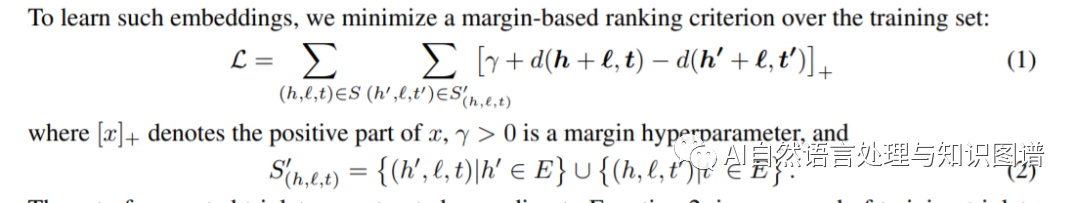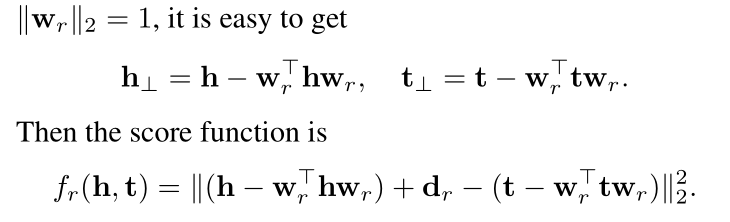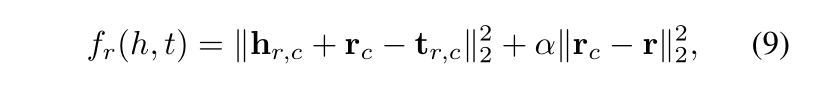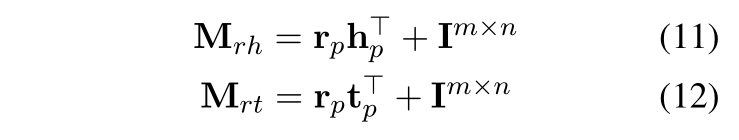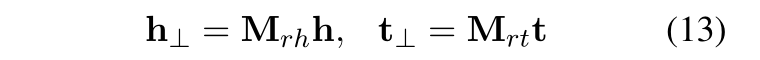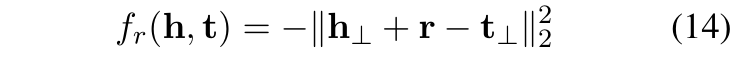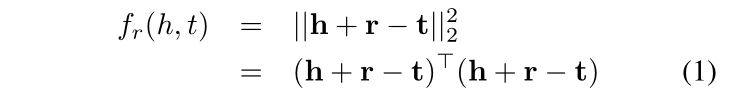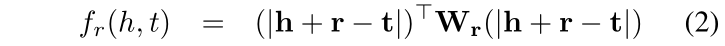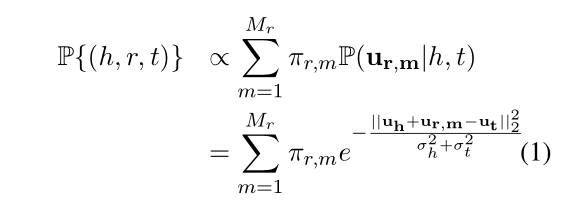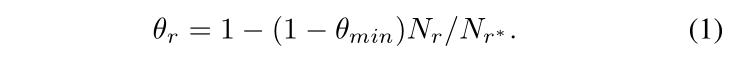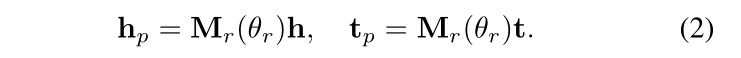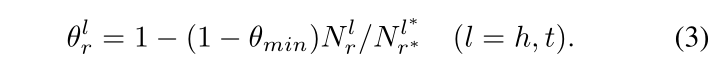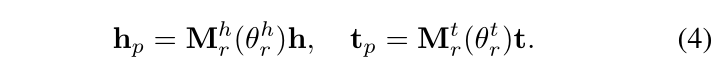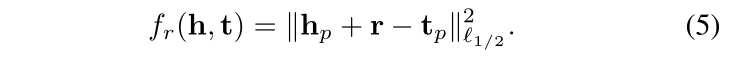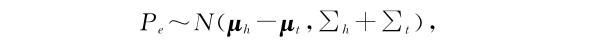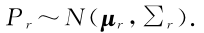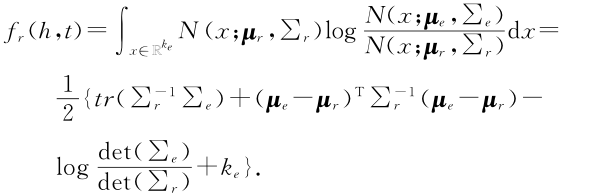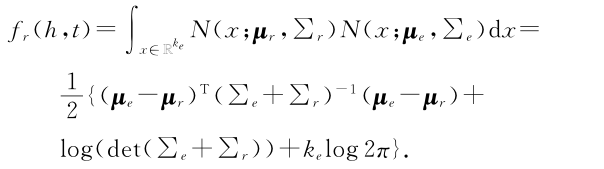知识表示学习Trans系列梳理(论文+代码)

2020 年 5 月 28 日 深度学习自然语言处理

来自：AI自然语言处理与知识图谱

知识表示学习Trans系列梳理

导语：本文将简短梳理知识表示学习Trans系列方法，包含TransE、TransH、TransR、TransD、TransA、TransG、TranSparse以及KG2E，并且结合Github清华开源的高星代码了解一下实现过程，以便能通过代码看出他们之间的联系和区别。

简谈TransE

Author：Bordes A, Usunier N, Garciaduran A, et al.

Title: Translating Embeddings for Modeling Multi-relational Data.

Accepted: Neural Information Processing Systems, NIPS2013.

翻译模型从 TransE 开始，并衍生出一系列模型。

首先来看看 TransE 的名字来源，它的论文标题是：Translating Embeddings for Modeling Multi-relational Data。从这个标题我们不难猜想出为什么简称为 TransE，以及为什么称之为翻译模型。除此之外，这篇论文也是始于2013年，发表在NIPS。

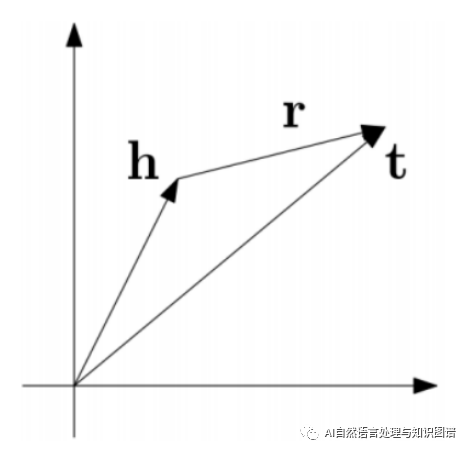
TransE 模型的基本思想就是把 relation 看做是 head 到 tail 的翻译，认为一个正确的知识三元组应该满足 h+ r =(约等于) t，而错误的不满足，通俗来讲就是头实体 embedding 加上关系 embedding 近似等于尾实体 embedding ，见下图，思想就是这么的简单但却高效。

TransE 定义了一个距离函数d(h + r, t)来衡量 h + r 和 t 之间的距离，我们也可以使用 L1 或 L2 范数。TransE采用最大间隔的方法，其目标函数如下：

其中，S是正确的三元组，S’是通过替换 h 或 t 所得错误的三元组。γ 是间隔距离超参数，[x]₊表示正值函数，即 x > 0 时，[x]₊= x；当 x ≤ 0 时，[x]₊= 0 。

我们来看一下OpenKE中的 TransE 代码部分：

最开始是在初始化__init__中定义了两个Embedding矩阵，分别为实体Embedding和关系Embedding，并且对其初始化。

self.ent_embeddings = nn.Embedding(self.ent_tot, self.dim)self.rel_embeddings = nn.Embedding(self.rel_tot, self.dim)对其采用xavier_uniform_初始化或者uniform_初始化的方式

接下来我们看下forward中的实现。

forward中主要是获取头尾实体以及关系的Embedding，其中头尾实体都是共用一个实体Embedding矩阵。
最主要的就是 _calc 这部分，其实也很简单，核心就是计算score，并且做个范数的约束。

   def _calc(self, h, t, r, mode):    if self.norm_flag:      h = F.normalize(h, 2, -1)      r = F.normalize(r, 2, -1)      t = F.normalize(t, 2, -1)    if mode != 'normal':      h = h.view(-1, r.shape[0], h.shape[-1])      t = t.view(-1, r.shape[0], t.shape[-1])      r = r.view(-1, r.shape[0], r.shape[-1])    if mode == 'head_batch':      score = h + (r - t)    else:      score = (h + r) - t    score = torch.norm(score, self.p_norm, -1).flatten()    return score
  def forward(self, data):    batch_h = data['batch_h']    batch_t = data['batch_t']    batch_r = data['batch_r']    mode = data['mode']    h = self.ent_embeddings(batch_h)    t = self.ent_embeddings(batch_t)    r = self.rel_embeddings(batch_r)    score = self._calc(h, t, r, mode)    if self.margin_flag:      return self.margin - score    else:      return score

在计算Loss部分，采用的是MarginLoss，margin参数值设置为5.0

# define the loss functionmodel = NegativeSampling(  model = transe,   loss = MarginLoss(margin = 5.0),  batch_size = train_dataloader.get_batch_size())

以上便是 TransE 的简短介绍和代码简析，我们接下来再看一下 TransH。

简谈TransH

Title: Knowledge graph embedding by translating on hyperplanes.

Author：Wang Z, Zhang J, Feng J, et al.

Accepted：National conference on artificial intelligence, AAAI 2014.

TransE 模型由于它简单高效所以取得了很大的突破，但是优点有时候也往往伴随着缺点，TransE 的对简单关系的建模效果显著，但是对复杂关系的建模效果却十分不理想，如1-N，N-1，N-N这样的复杂关系，所以才提出了后续的很多模型变种，TransH 便是其中一个。

为了更好的理解上面所述的复杂关系，我们在此说明，按照知识库中关系两端连接实体的数量，可以将关系类型划分为 1-1、 1-N、N-1 和 N-N 四种。以 N-1 类型关系为例，指的是该类型关系中的一个尾实体会平均对应多个头实体，其他的类推。

接下来我们看一下为什么 TransE 对复杂关系建模效果不好？以及 TransH 的建模思想。

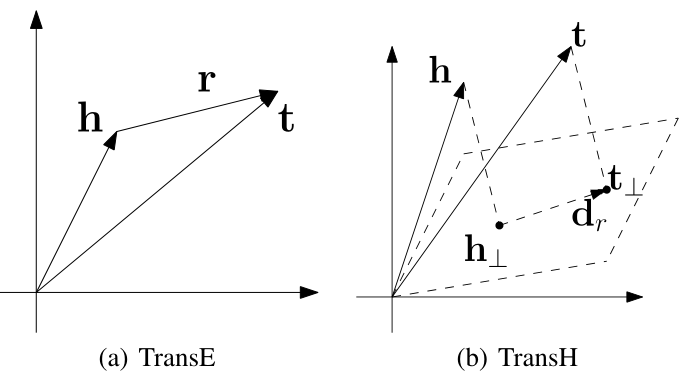
上面说 TransE 对复杂关系建模不好，假定我们存在多个关系三元组，其中关系和尾实体都是固定不变的，而头实体对应多个，这就是N-1的关系，那么根据 TransE 的思想(上图a)建模，多个头实体将会得到非常相近的向量表示，可能近乎为统一含义，这对于不同业务下的不同场景是不合理的。

TransH 的动机就是解决这种复杂关系，那么它具体是怎么解决的呢？

TransH 的核心思想是对于关系每一个 r，有一个超平面

回到我们上面的N-1的复杂关系问题，对于三元组(h, r, t)和(h1, r, t)，根据 TransE 的思想, h1 = h。而对于 TransH 来说，只需要满足 h 和 h1 在关系 r 的超平面上的投影相同就行啦，这样就可以区分出 h 和 h1，两个的向量表示是不同的。

下面是 TransH 的头尾实体映射的向量计算以及损失函数。

看下 TransH 名称的由来，translating on hyperplanes(超平面)

我们来看一下OpenKE中的 TransH 代码部分：

最开始是在初始化__init__中定义了三个Embedding矩阵，并且对其初始化。这与TransE 不同的就是多了一个Embedding，代表的是关系的超平面Embedding。

self.ent_embeddings = nn.Embedding(self.ent_tot, self.dim)self.rel_embeddings = nn.Embedding(self.rel_tot, self.dim)self.norm_vector = nn.Embedding(self.rel_tot, self.dim)对其采用xavier_uniform_初始化或者uniform_初始化的方式

接下来我们看下 forward 中的实现。

这部分的代码和 TransE 大致相同，多了一个 TransH 的核心部分，就是头尾实体映射到超平面的向量转化，即 _transfer 函数实现。

 def _calc(self, h, t, r, mode):    same as TransE      def _transfer(self, e, norm):    norm = F.normalize(norm, p = 2, dim = -1)    if e.shape[0] != norm.shape[0]:      e = e.view(-1, norm.shape[0], e.shape[-1])      norm = norm.view(-1, norm.shape[0], norm.shape[-1])      e = e - torch.sum(e * norm, -1, True) * norm      return e.view(-1, e.shape[-1])    else:      return e - torch.sum(e * norm, -1, True) * norm
  def forward(self, data):    batch_h = data['batch_h']    batch_t = data['batch_t']    batch_r = data['batch_r']    mode = data['mode']    h = self.ent_embeddings(batch_h)    t = self.ent_embeddings(batch_t)    r = self.rel_embeddings(batch_r)    r_norm = self.norm_vector(batch_r)    h = self._transfer(h, r_norm)    t = self._transfer(t, r_norm)    score = self._calc(h ,t, r, mode)    if self.margin_flag:      return self.margin - score    else:      return score

在计算Loss部分，采用的是MarginLoss，margin参数值设置为4.0

# define the loss functionmodel = NegativeSampling(  model = transh,   loss = MarginLoss(margin = 4.0),  batch_size = train_dataloader.get_batch_size())

简谈TransR

Title: Learning Entity and Relation Embeddings for Knowledge Graph Completion

Author：Lin Y, Liu Z, Zhu X, et al.

Accepted：National conference on artificial intelligence, AAAI 2015.

TransR 方法的提出是在 TransE 和 TransH 的基础之上，TransE 和TransR 虽然多取得了很大的进步，但是他们实体和关系都是映射在同一语义空间中，然而实体包含多种属性，不同的关系对应不同的实体属性，因此，在实体空间中，有些实体是相似的，因而彼此接近，但某些特定实体属性却有相当大的不同，因而在相关的关系空间中彼此相距甚远，TransR 的提出缘起于此。

所谓 TransR 是指将实体和关系映射到不同的语义空间，并且关系不再是单一的，而是多个关系空间，头尾实体的翻译也是在相应的关系空间中完成。这个 R 代表的是 Relation Space。

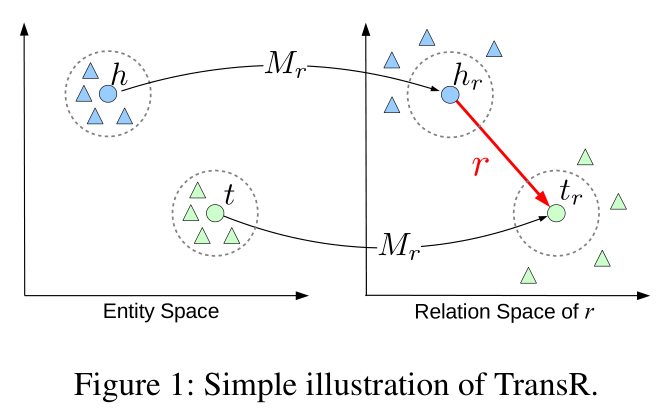
下面是 TransR 的模型图，我们能够看出实体和关系表示在不同的语义空间中。

对于每一个三元组(h, r, t)，将头尾实体表示在实体空间，将关系表示在关系空间，并且，对于每一个关系 r，存在一个映射矩阵 Wr，通过这个矩阵将 h, t 映射到关系 r 所在空间，得到 hr 和 tr，使 hr + r = tr。在这种关系的作用下，具有这种关系的头/尾实体彼此接近(彩色的圆圈)，不具有此关系（彩色的三角形）的实体彼此远离。

下面是一些公式的定义。

在本文中，TransR 还进行了变体，叫做 CTransR，其中的 C 是 Cluster，表示聚类聚类。具体来说，仅通过一个关系向量不足以满足头尾实体对的多样性表示，比如关系（location_location_contains）其实包含 country-city、country-university、continent-country 等多种含义。

因此对于某一种关系的全部实体对（h，t），采用聚类的方式得到多种聚类结果，学习每种聚类结果的关系表示，用 TransE模型训练得到的 h, t，将 h-t 作为它的表示，对于每一类的关系都有一个映射矩阵 Mr 和一个向量表示 r，其他和 TransR 一样。

具体的定义如下：

接下来，看一下 TransR 的代码。

最开始是在初始化__init__中定义了三个Embedding矩阵，并且对其初始化。这里的

transfer_matrix ，代表的是不同关系的Embedding。

self.ent_embeddings = nn.Embedding(self.ent_tot, self.dim_e)self.rel_embeddings = nn.Embedding(self.rel_tot, self.dim_r)self.transfer_matrix = nn.Embedding(self.rel_tot, self.dim_e * self.dim_r)对其采用xavier_uniform_初始化或者uniform_初始化的方式

接下来我们看下 forward 中的实现。

这部分的代码和其他的大致相同，多了一个 TransR 的核心部分，就是头尾实体映射到不同关系空间，即 _transfer 函数实现。

  def _calc(self, h, t, r, mode):    same as TransE
  def _transfer(self, e, r_transfer):    r_transfer = r_transfer.view(-1, self.dim_e, self.dim_r)    if e.shape[0] != r_transfer.shape[0]:      e = e.view(-1, r_transfer.shape[0], self.dim_e).permute(1, 0, 2)      e = torch.matmul(e, r_transfer).permute(1, 0, 2)    else:      e = e.view(-1, 1, self.dim_e)      e = torch.matmul(e, r_transfer)    return e.view(-1, self.dim_r)
  def forward(self, data):    batch_h = data['batch_h']    batch_t = data['batch_t']    batch_r = data['batch_r']    mode = data['mode']    h = self.ent_embeddings(batch_h)    t = self.ent_embeddings(batch_t)    r = self.rel_embeddings(batch_r)    r_transfer = self.transfer_matrix(batch_r)    h = self._transfer(h, r_transfer)    t = self._transfer(t, r_transfer)    score = self._calc(h ,t, r, mode)    if self.margin_flag:      return self.margin - score    else:      return score

在计算Loss部分，采用的是MarginLoss，margin参数值设置为4.0

# define the loss functionmodel_r = NegativeSampling(  model = transr,  loss = MarginLoss(margin = 4.0),  batch_size = train_dataloader.get_batch_size())

简谈TransD

Title: Knowledge graph embedding via dynamic mapping matrix

Author：Ji G, He S, Xu L, et al.

Accepted：ACL 2015.

TransD 方法的提出是在 TransR 的基础之上，虽然 TransR 相对于前两种方法有显著的效果，但是也存在明显的缺点，如下：

(1) 在同一关系 r 下, 头尾实体共用相同的投影矩阵，然而，一个关系的头尾实体存在很大的差异，例如（美国，总统，奥巴马），美国是一个实体，代表国家，奥巴马是一个实体，代表的是人物。

(2) TransR 仅仅让给投影矩阵与关系有关是不合理的，因为投影矩阵是头尾实体与关系的交互过程，应该与实体和关系都相关。

(3) TransR 模型的参数急剧增加，计算的时间复杂度大大提高。

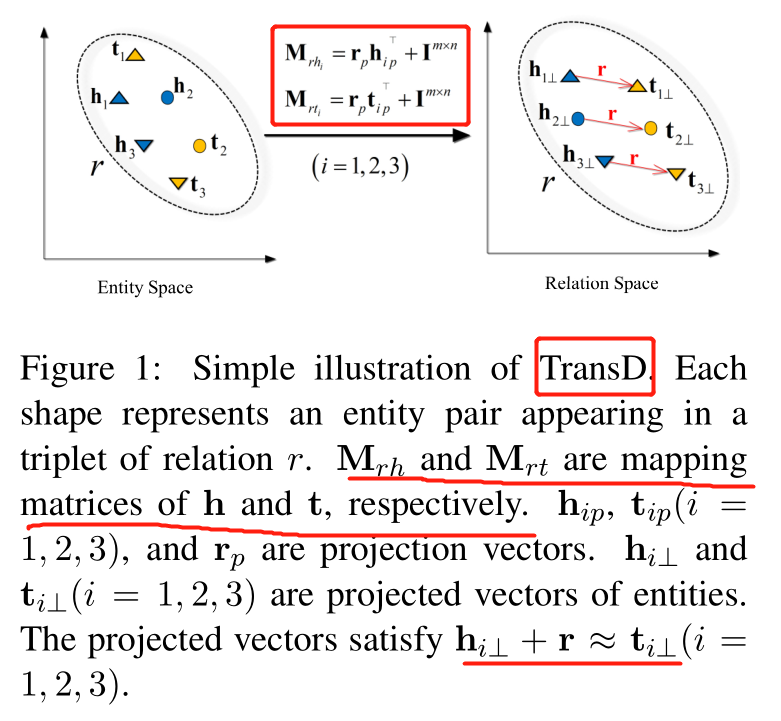
下面是 TransD 的模型图。

我们来看下 TransD 的模型思想，给定一个三元组(h, r, t)，TransD 将头尾实体分别投影到关系空间得到投影矩阵 Mrh 和 Mrt ,这样得到的投影矩阵便与实体和关系都有关系。获取投影矩阵之后，和 TransR 一样，计算头尾实体的投影向量。

接下来，看一下 TransD 的代码。最开始是在初始化__init__中定义了四个 Embedding 矩阵，并且对其初始化。这里的 ent_transfer 和 rel_transfer 代表的是实体关系转换矩阵。

self.ent_embeddings = nn.Embedding(self.ent_tot, self.dim_e)self.rel_embeddings = nn.Embedding(self.rel_tot, self.dim_r)self.ent_transfer = nn.Embedding(self.ent_tot, self.dim_e)self.rel_transfer = nn.Embedding(self.rel_tot, self.dim_r)对其采用xavier_uniform_初始化或者uniform_初始化的方式

接下来我们看下 forward 中的实现。

  def _transfer(self, e, e_transfer, r_transfer):    if e.shape[0] != r_transfer.shape[0]:      e = e.view(-1, r_transfer.shape[0], e.shape[-1])      e_transfer = e_transfer.view(-1, r_transfer.shape[0], e_transfer.shape[-1])      r_transfer = r_transfer.view(-1, r_transfer.shape[0], r_transfer.shape[-1])      e = F.normalize(        self._resize(e, -1, r_transfer.size()[-1]) + torch.sum(e * e_transfer, -1, True) * r_transfer,        p = 2,         dim = -1      )            return e.view(-1, e.shape[-1])    else:      return F.normalize(        self._resize(e, -1, r_transfer.size()[-1]) + torch.sum(e * e_transfer, -1, True) * r_transfer,        p = 2,         dim = -1      )
  def forward(self, data):    batch_h = data['batch_h']    batch_t = data['batch_t']    batch_r = data['batch_r']    mode = data['mode']    h = self.ent_embeddings(batch_h)    t = self.ent_embeddings(batch_t)    r = self.rel_embeddings(batch_r)    # 实体和关系不同的空间表示    h_transfer = self.ent_transfer(batch_h)    t_transfer = self.ent_transfer(batch_t)    r_transfer = self.rel_transfer(batch_r)    # 计算投影矩阵和投影实体向量    h = self._transfer(h, h_transfer, r_transfer)    t = self._transfer(t, t_transfer, r_transfer)    score = self._calc(h, t, r, mode)    if self.margin_flag:      return self.margin - score    else:      return score

‍

在计算Loss部分，采用的是MarginLoss，margin参数值设置为4.0

# define the loss functionmodel = NegativeSampling(  model = transd,   loss = MarginLoss(margin = 4.0),  batch_size = train_dataloader.get_batch_size())

简谈TransA

Title: TransA: An Adaptive Approach for Knowledge Graph Embedding

Author：Xiao H, Huang M, Hao Y, et al.

TransA模型认为前述的模型都存在以下两个问题，(1) 损失函数中的距离度量太过简单，不具备灵活性（2）由于损失函数过于简单，实体和关系向量的每一维都等同对待，但是不同维度的重要度不一样，有些维度效果好，有些维度可能是噪音。

具体看一下这两个问题：

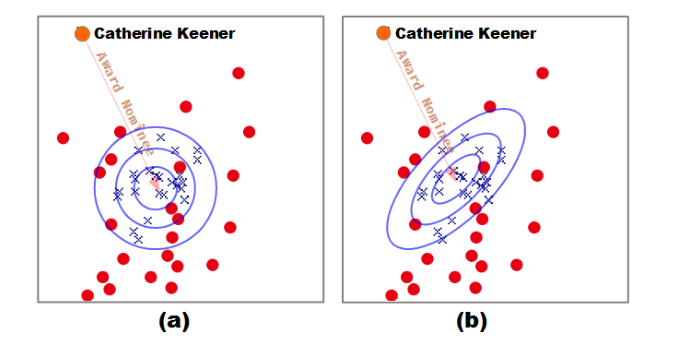
下图是采用 PCA 降维呈现的向量可视化界面，是匹配演员提名奖的尾实体，蓝色可以看为正例，即匹配，红色圆点代表为匹配，即负例。a/b 分别呈现的是 TransE 和 TransA，TransE 采用类似欧氏距离度量方式，分错了7个点，而 TransA采用马氏距离分错了三个点，减少了四个错误划分。

上述方法中实体和关系向量的每一维都等同对待，但是不同维度的重要度不一样，有些维度效果好，有些维度可能是噪音，因此将其等同对待是不合理的。

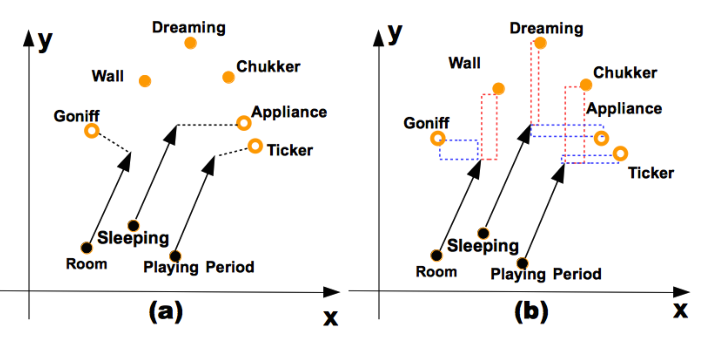
来看下图，实点表示正确匹配，空心点表示错误匹配，箭头表示某种关系(HasPart)，我们来看一个例子，在图(a)中采用欧式距离得到的结果中有一个三元组(Sleeping，HasPart, Appliance)，但是它是错误的，正确的三元组是(Sleeping，HasPart, Dreaming)。TransA 为了不等同对待向量的每一维，对向量维度加权，赋予不同的权重，在图(b)中对 xy 轴进行了拆解，对 y 轴加权，对 x轴降权，这样x轴就有一个较小的loss，会向正确的三元组方向学习。

具体的来看一下：以往的TransE是公式(1)，公式(2)是TransA的损失函数，其中增加了Wr权重矩阵，并且是与关系r相关的非负权值矩阵，除此之外，对于 h+r 和 t 采用了绝对值的方式。

简谈TransG

Title:TransG : A Generative Mixture Model for Knowledge Graph Embedding

Author：Xiao H, Huang M, Zhu X.

Accepted：ACL 2016.

TransD 模型的提出是为了解决关系的多种语义问题，和上面的 TransR 解决的问题类似，一种关系可能存在多种语义表达。

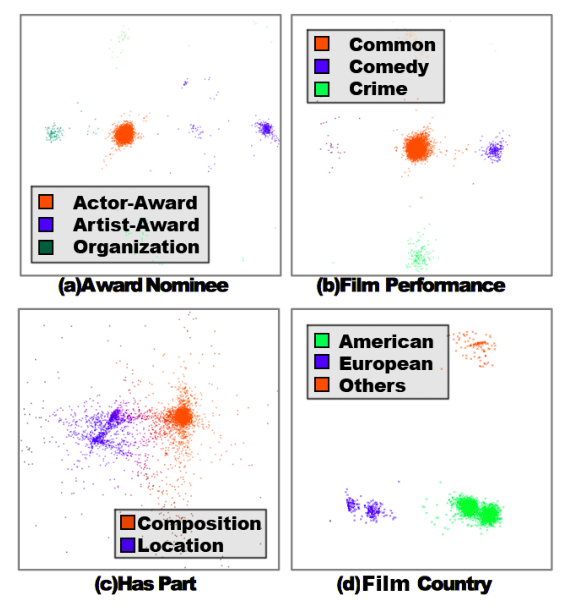
我们来看一个简单的实验，如下图。下图是对TransE关系向量聚类的可视化结果，从图中能够看出，每一种关系都聚类为不同的簇，每一个簇代表的是某种潜在的语义表示，说明关系存在多种潜在的语义表示，如图(d)的关系 Film Country，至少存在三个潜在的语义表示，分别为美国、欧洲、其他国家。

TransG具体是怎么来做的？TransG认为既然一种关系存在多种语义表达，那么将每种语义采用高斯分布来刻画。具体的公式定义如下，Mr代表的是潜在语义关系数量，

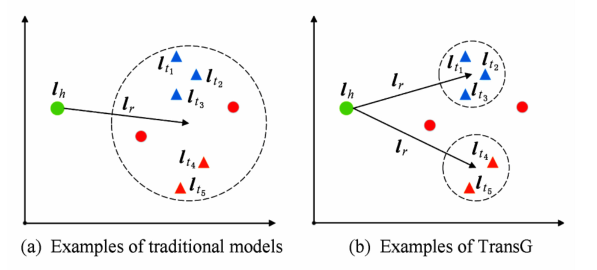
最后来看下传统模型和 TransG 模型的比较，如下图，其中三角形为正确的尾实体，圆点为错误的尾实体，不同颜色的三角代表不同的语义表达。(a) 为传统模型示例，由于将关系 r 的所有语义混为一谈，导致错误的实体无法被区分，(b) 中为 TransG的模型示例，TransG 利用高斯分布刻画不同语义关系，从而能够区分出错误实体。

简谈TranSparse

Title: Knowledge Graph Completion with Adaptive Sparse Transfer Matrix

Author：Ji G, Liu K, He S, et al

Accepted：AAAI 2016.

实体库中实体和关系的 异质性(heterogeneous) 和 不平衡性(unbalanced) 是知识表示学习的两个难题。

异质性(heterogeneous)：关系链接实体的数量不一致，有的很多，有的很少。

不平衡性(unbalanced)：某些关系头尾实体的种类和数量可能差别巨大。

如下图是两种问题在FB15k的关系统计

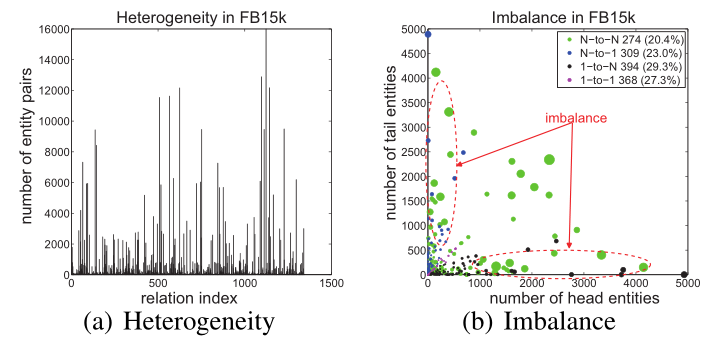
在以前的方法中，简单或者复杂关系都有相同数量参数的矩阵。然而，复杂的关系连接更多的头尾实体，比简单的关系更有意义。因此，复杂的关系需要更多的参数来充分学习，而简单的关系需要更少的参数来适当地学习，这就可以防止模型不完全拟合或过度拟合。TranSparse 认为关系的复杂性链接三元组(或实体)的数量成正比，因为链接的数据越多，它包含的知识就越多。

TranSparse 模型是在 TransR 的模型基础之上，采用稀疏矩阵代替了 TransR 中的稠密矩阵，因为采用稀疏矩阵 Mr，所以命名为 TranSparse，针对异质性问题提出TranSparse(share)，针对不平衡性提出 TranSparse(separate)。

TranSparse(share)：对于每一个关系，有翻译向量 r 和稀疏矩阵 Mr，稀疏矩阵的稀疏度由关系链接的实体对数量决定，稀疏度 θr 的定义如下，其中 Nr 表示关系链接的实体对的数量，Nr* 表示最大实体对的数量(关系链接最多的实体对)，θmin 为稀疏度超参数，取值在 [0, 1] 之间，根据下面的公式(2)可以得到头尾实体的投影矩阵。

TranSparse(separate)：对于每一个关系，设置两个投影矩阵，分别为头实体 Mrh 和尾实体 Mrt，两者的稀疏度 θrl 和上面的有所改动，具体如下，其中 Nrl 表示关系 r 在位置 l 处链接的实体的数量，Nr*l 表示 Nrl 中最大的数，θmin 为稀疏度超参数，取值在 [0, 1] 之间，根据下面的公式(4)可以得到头尾实体的投影矩阵。

以上两个方法的损失函数均为如下定义：

简谈KG2E

Title: Learning to Represent Knowledge Graphs with Gaussian Embedding

Author：He S, Liu K, Ji G, et al.

Accepted：ACM 2015.

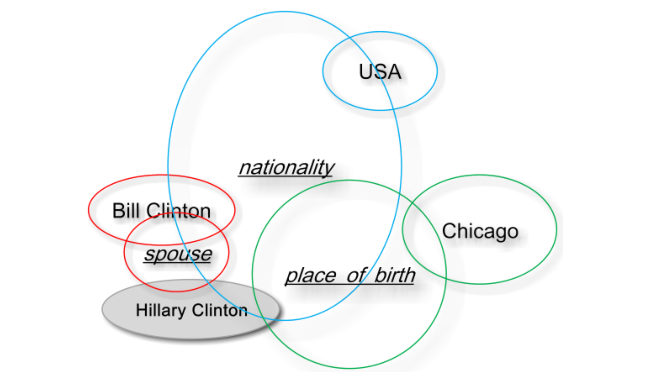
作者认为以前的方法都是将实体和关系嵌入到点向量空间中，这些模型总是以同样的方式看待所有的实体和关系，而作者认为实体库中的实体和关系本身就就存在不确定性，以前的方法模型忽略了这一不确定性。

针对这种不确定性，文中给出了图示，如下图所示，带有下划线的表示关系，每个圆圈代表不同实体和关系的表示，他们分别于 Bill Clinton构成了三元组，圆圈越大代表其不确定性越大，从图中我们能够看出 nationality这个关系的不确定性是最大的。

基于上述不确定性问题，本文提出 KG2E，与以往不同的是不再采用点空间，而是基于密度，采用高斯分布表示实体和关系，其中均值表示其所处的中心位置，而协方差可以恰当的表示其不确定度。

KG2E使用 h-t 表示头尾实体之间的关系，实体可以用一个概率分布表示，如下：

关系 r 也同样是一个高斯分布：

可以根据上述两个概率分布估算三元组的得分。

KG2E考虑了两种计算概率相似度的方法：KL-距离(KL-divergence)和期望概率(expected likelihood)。

KL距离是一种不对称相似度，得分函数定义如下：

期望概率是一种对称相似度，得分函数如下：

结束语

小白用几天的时间学习了知识表示学习的8篇典型论文，包含TransE、TransH、TransR、TransD、TransA、TransG、TranSparse以及KG2E，并简单看了下Github 的开源代码 OpenKE，每种方法都有各自的优势与劣势，有的适合研究却不适合业界应用，有的在业界也可以大胆尝试，看完之后，收获不小，整理为这一篇文章，分享给大家，文章篇幅较长，可能存在书写错误之处，还请见谅。

参考资料

Bordes A, Usunier N, Garcia-Duran A, et al. Translating embeddings for modeling multi-relational data[C]//Advances in neural information processing systems. 2013: 2787-2795.
Wang Z, Zhang J, Feng J, et al. Knowledge graph embedding by translating on hyperplanes[C]//Twenty-Eighth AAAI conference on artificial intelligence. 2014.
Lin Y, Liu Z, Sun M, et al. Learning entity and relation embeddings for knowledge graph completion[C]//Twenty-ninth AAAI conference on artificial intelligence. 2015.
Ji G, He S, Xu L, et al. Knowledge graph embedding via dynamic mapping matrix[C]//Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). 2015: 687-696.
Xiao H, Huang M, Hao Y, et al. TransA: An Adaptive Approach for Knowledge Graph Embedding[J]. arXiv: Computation and Language, 2015.
Xiao H, Huang M, Hao Y, et al. TransG : A Generative Mixture Model for Knowledge Graph Embedding[J]. arXiv: Computation and Language, 2015.
Ji G, Liu K, He S, et al. Knowledge graph completion with adaptive sparse transfer matrix[C]. national conference on artificial intelligence, 2016: 985-991.
He S, Liu K, Ji G, et al. Learning to represent knowledge graphs with gaussian embedding[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. 2015: 623-632.
刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247-261.
https://github.com/thunlp/OpenKE