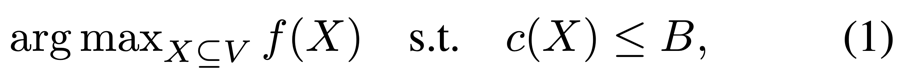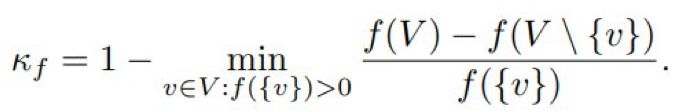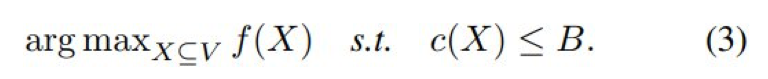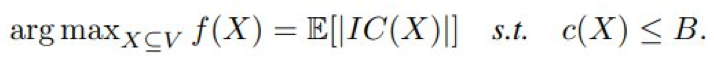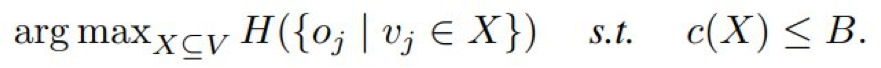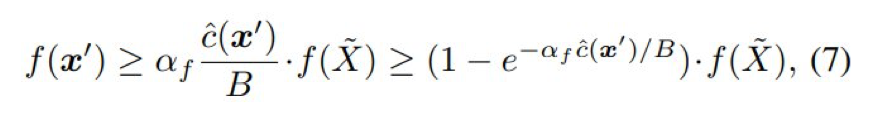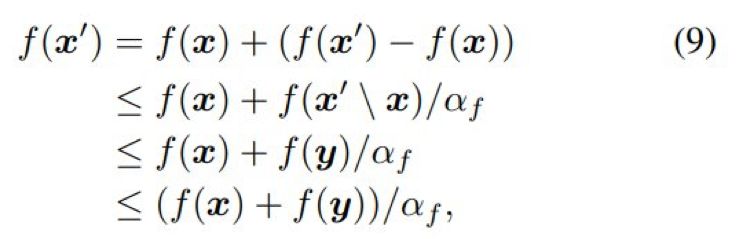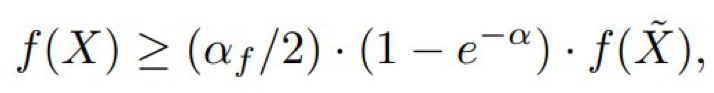日前,AAAI 2020 已在美国纽约隆重召开。
不久之前,大会官方公布了今年的论文收录信息:
收到 8800 篇提交论文,评审了 7737 篇,接收 1591 篇,接收率 20.6%。
为向读者们分享更多的优质内容、促进学术交流,机器之心策划了多期AAAI 2020 论文线上分享。
近日,机器之心邀请了南京大学人工智能学院研究助理卞超通过线上分享的方式介绍他们入选 AAAI 2020 的研究论文《An Efficient Evolutionary Algorithm for Subset Selection with General Cost Constraints》。
这篇论文提出了一个高效的演化算法 EAMC,来解决一般约束下的子集选择问题。
本文将对这项研究成果进行介绍。
论文地址:
http://www.lamda.nju.edu.cn/qianc/aaai20-eamc-final.pdf
子集选择问题是一个 NP-hard 问题,并且具有很多应用场景,比如最大覆盖、影响力最大化和传感器放置。
该问题的目标是从 n 个元素中,选择满足约束 c 的一个子集,使得目标函数 f 的值最大:
![]()
其中 f 和 c 都是单调的,但并不一定满足子模性。
针对这类问题,现有的代表性算法有广义贪心算法和 POMC。
广义贪心算法耗时较短,但是受限于它的贪心行为,其找到的解质量往往一般;
POMC 作为随机优化算法,可以使用更多的时间来找到质量更好的解,但是其缺乏多项式的运行时间保证。
为此,这篇 AAAI 2020 论文提出了一个高效的演化算法 EAMC。
通过优化一个整合了 f 和 c 的代理函数,它可以在多项式时间内找到目前已知最好的近似解。
研究者还在最大覆盖、影响力最大化和传感器放置等任务上进行了实验,结果表明该算法的表现优于广义贪心算法。
令 R 和 R^+ 分别表示实数集和非负实数集。
给定一个全集 V = {v_1, v_2, ... , v_n},研究的问题是在 V 的子集上的函数 f : 2^V → R。
如果 ∀X ⊆ Y 时 f(X) ≤ f(Y),则称集合函数 f 是单调的,这说明往一个集合添加更多元素时永远不会导致函数值减少。
不失一般性地,假设,这些单调函数是归一化的,即 f(∅) = 0。
如果对于任意 X ⊆ Y ⊆ V 和 v ∉ Y,有 f(X∪{v})−f(X)≥f(Y∪{v})−f(Y),则称集合函数 f 是子模 (submodular) 函数,这表示该函数具有增益递减性质,即向集合 X 增加元素时所带来的收益大于向 X 的超集 Y 添加同样的元素。
对于一个广义的集合函数 f,如定义 1 所示的子模比(submodularity)的概念可用于度量 f 所具有的子模性的程度。
当 f 单调时,有这两个结论:
(1)0 ≤ α_f ≤ 1;
(2)α_f = 1 当且仅当 f 是子模函数。
注意,在衡量 f 与子模性的相近程度方面还存在其它一些符号,比如 Krause and Cevher 2010; Das and Kempe 2011; Zhou and Spanos 2016 等中使用的符号。
定义 1:
子模比。
非负集合函数 f 的子模比定义为:
![]()
定义 2 所代表的总曲率描述了单调子模函数 f 与模块度(modularity)的相近程度。
很容易验证 1 ≥ 1 – κ_f ≥ 0。在这篇论文中,研究者用
κ_f 表示广义 单调函数。
根据式(2),如果没有子模性,则 1/α_f ≥ 1 – κ_f ≥ 0 成立。
定义 2:
总曲率。
定义单调子模集合函数 f 的总曲率为:
![]()
定义 3 给出了本研究所关注的问题,即最大化单调目标 f,使得单调成本函数 c 的上界处在预算 B 的约束下。
f 和 c 并不必须都是子模函数。
假设 f 由一个 value oracle 给定,即对于任意子集 X,都有一个算法可以查询 oracle 以得到 f(X) 的值。
和之前一些论文一样,研究者也假设精确的成本函数 c 是无法得到的,而只能得到一个 ψ(n) 近似 cˆ,其中 ∀X ⊆ V : c(X) ≤ cˆ(X) ≤ ψ(n) · c(X)。
这是因为在某些现实应用中,精确计算 c 所需的时间可能呈指数增长。
定义 3:
文本所研究的广义问题。
给定一个单调目标函数 f : 2^V → R^+、一个单调成本函数 c : 2^V → R^+ 以及预算 B,目标是找到:
![]()
这篇论文在三种应用上通过实验研究了单调子模目标函数。
第一种应用是最大覆盖问题。
给定一组覆盖了元素全域的集合,最大覆盖任务的目标是在一定成本预算下选择出某些集合并使得这些集合的并集是最大的。
可以很容易验证:
f 是单调的子模函数。
定义 4:
最大覆盖。
给定一个元素集合 U、U 的一组子集 V ={S1, S2, . . . , Sn}、一个单调成本函数 c : 2^V →R^+ 以及预算 B,目标是找到:
![]()
第二种应用是影响力最大化,其目标是识别社交网络中有影响力的用户集。
首先定义一个有向图 G = (V, E) 来表示社交网络,其中每个节点都是一个用户,每条边 (u, v) ∈ E(带有概率 p_{u,v})表示用户 u 到 v 的影响力强度。
给定预算 B,影响力最大化的目标是找到 V 的一个子集 X,使得由源自 X 的传播而激活的节点的预期数量最大。
独立级联(Independence Cascade/IC)是一种基础的传播模型。
其使用一个集合 A_t 来记录在时间 t 激活的节点;
在时间 t+1,u ∈ A_t 的每个未激活的邻近节点 v 都有 p_{u,v} 的概率被激活。
这个过程不断重复,直到到达没有节点再被激活的时间。
将由 X 的传播而激活的节点集记为 IC(X),这是一个随机变量。
目标 E[|IC(X)|] 被称为影响力传播度(influence spread),这是一个单调子模函数,其中 E[·] 是指随机变量的期望。
定义 5:
影响力最大化。
给定一个有向图 G = (V, E),对于 (u, v)∈E,边概率为 p_{u,v};
以及单调成本函数 c : 2^V →R^+ 和预算 B,目标是找到:
![]()
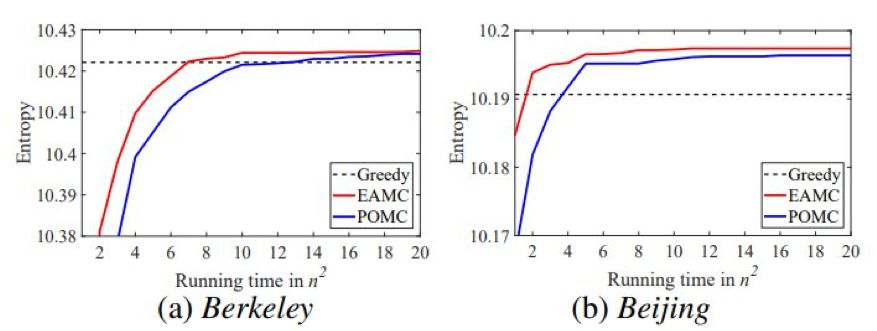
第三个应用是传感器放置,其目标是决定有限数量的传感器的放置位置,使得不确定度能最大限度地降低。
令 o_j 表示一个随机变量,其代表通过在位置 v_j 安装传感器而收集到的观察数据。
注意,对于已经观察到子集 S 的随机变量的总集合 U,其条件熵(即剩余的不确定度)为 H(U | S) = H(U) − H(S),其中 H(·) 表示熵。
因此,这个任务的目标是选择一个位置子集 X,使得 {o_j | v_j ∈ X} 的熵最大。
已知熵 H(·) 是一个单调子模函数。
定义 6:
传感器放置。
给定 n 个位置 V = {v_1, v_2, ... , v_n}、单调成本函数 c : 2^V →R^+ 和预算 B,目标是找到:
![]()
对于这些应用,成本限制可能是简单的规模限制,即 c(X) = |X|;
或一般的线性成本限制,即![]() 。
但在某些情况中,这个限制可能更加复杂,比如路径限制,这是单调非子模的。
举个例子,在移动机器人传感领域,需要计入在不同位置之间移动的成本以及在这些位置进行测量的成本。
用图 G = (V, E) 表示所有位置的路径网络,其中 c_e 表示穿过一条边 e ∈ E 的成本,c_v 表示访问一个节点 v ∈ V 的成本。
成本函数为
。
但在某些情况中,这个限制可能更加复杂,比如路径限制,这是单调非子模的。
举个例子,在移动机器人传感领域,需要计入在不同位置之间移动的成本以及在这些位置进行测量的成本。
用图 G = (V, E) 表示所有位置的路径网络,其中 c_e 表示穿过一条边 e ∈ E 的成本,c_v 表示访问一个节点 v ∈ V 的成本。
成本函数为![]() ,
其中
,
其中 ![]() 是
访问 X 中每个节点至少一次的最短行走的成本,这通常是非子模的,而且无法在多项式时间中得到准确的计算。
本文的实验中,线性约束和路由约束都会用到。
这一节介绍研究者为最大化有单调成本限制的单调函数所提出的一种简单演化算法:
EAMC。
EAMC 不会最大化式(3)中的 f,而是引入了一个替代目标 g,并对其进行最大化,用数学表示为:
是
访问 X 中每个节点至少一次的最短行走的成本,这通常是非子模的,而且无法在多项式时间中得到准确的计算。
本文的实验中,线性约束和路由约束都会用到。
这一节介绍研究者为最大化有单调成本限制的单调函数所提出的一种简单演化算法:
EAMC。
EAMC 不会最大化式(3)中的 f,而是引入了一个替代目标 g,并对其进行最大化,用数学表示为:
![]()
可以看到,g 同时纳入了原有的目标函数 f 以及成本 cˆ。
更小的 cˆ 值和更大的 f 值都会导致 g 的值更大。
在优化过程中,EAMC 会保留一个种群 P,然后新生成的解 x' 只会与 bin(|x'|) 中解进行比较。
bin(|x'|) 的定义为:
![]()
也就是说,x' 只与 P 中与 x' 有同样大小的解相比。
这样的设置会让这个解群 P 更加多样化,由此能够提升该算法的搜索能力。
由于问题式 (3) 需要在满足预算限制的同时实现 f 的最大化,所以 EAMC 只会考虑满足 cˆ(x')≤B 的 x';
在运行过程中,除了有最大 g 值的解之外,每个 bin 都保留有截至目前所生成的最大 f 值的解。
算法 3 描述了 EAMC 的执行过程。
从空集 0^n 开始(行 1),不断尝试改善每个 bin 中的解的 g 值(行 2-21)。
在每次迭代中,通过随机翻转从当前 P 中选出的解 x 来生成一个新的解 x'(行 3-4);
而且只有当 x' 满足限制条件时才会被包含进 P 中(行 5)。
如果 bin(|x'|) = ∅,则将 x' 添加进 P,并将 u^|x'| 和 v^|x'| 分别用于保留有目前所生成的最大 g 和 f 值的大小为 |x'| 的两个解(行 7-9);
否则,x' 与 bin(|x'|) 中的解进行比较,如果截至目前生成的最大 g 或 f 得到提升,则更新 bin(|x'|)(行 10-18)。
可以看到,每个 bin(i) 都只包含解 u^i 和 v^i,它们可能是一样的。
在 T 轮迭代后,P 中有最大 f 值的解被输出(行 22)。
注意,因为行 5,P 中的所有解都必须满足约束。
![]()
EAMC 需要知道子模比 α_f,因为替代目标 g 需要使用它。
对于子模的 f,α_f = 1。
对于非子模的 f,精确计算 α_f 可能需要指数级的时间,不过可以在 α_f 上使用一个下限来替代。
注意,α_f 的这个下限在一些单调非子模应用中已被推导出来,比如贝叶斯实验设计和行列式函数最大化。
这一节为 EAMC 的一般近似界给出了证明,如定理 3 所示。
相比于定理 2,EAMC 能实现与 POMC 同样的近似保证,即![]() ,
但预期的运行时间是多项式的上限。
其证明依赖于引理 1,可以直观地看到,这意味着对于任意子集,某个特定项的包含都至少能将 f 提升一定量,这个量与离最佳结果的当前距离成比例。
这里假设 ∀v ∈ V : cˆ({v}) ≤ B;
因为在优化前可以将任意 cˆ({v}) > B 的 v 直接移除。
,
但预期的运行时间是多项式的上限。
其证明依赖于引理 1,可以直观地看到,这意味着对于任意子集,某个特定项的包含都至少能将 f 提升一定量,这个量与离最佳结果的当前距离成比例。
这里假设 ∀v ∈ V : cˆ({v}) ≤ B;
因为在优化前可以将任意 cˆ({v}) > B 的 v 直接移除。
![]()
![]()
证明。
通过分析如下定义的量 J_max,可以证明该定理。
![]()
令 P_max 表示 EAMC 运行期间种群 P 的最大规模。
研究者首先表明,在至多 enP_max 个预期数量的迭代后,J_max ≥ 1。
很容易看到,解 0^n 将总是位于 P 中,因为只有同样规模大小的解可以进行比较,而 0^n 是大小为 0 为唯一解。
根据引理 1,翻转一个 0^n 的一个特定 0 位(即添加一个特定项)可以生成一个新的解 x',使得:
![]()
其中由于 ∀r ∈ R : 1 − r ≤ e^−r,后一个不等号是成立的。
在每轮迭代中,x' 都至少能以
![]() 的概率生成,其中 1/P_max 是从解群选出 0^n 的概率的下界,
的概率生成,其中 1/P_max 是从解群选出 0^n 的概率的下界,![]() 是在保持其它位不变的同时翻转 0^n 的特定比特的概率。因此,生成 x' 的预期迭代次数至多为 enP_max。注意,根据式 (6) 和 (7),
是在保持其它位不变的同时翻转 0^n 的特定比特的概率。因此,生成 x' 的预期迭代次数至多为 enP_max。注意,根据式 (6) 和 (7),![]() 。如果 x' 包含在 P 中,则有 J_max ≥ 1;否则,bin(1) 中必然存在一个 g 值更大的解,这意味着 J_max ≥ 1。
。如果 x' 包含在 P 中,则有 J_max ≥ 1;否则,bin(1) 中必然存在一个 g 值更大的解,这意味着 J_max ≥ 1。
假设当前的 J_max = i。
根据算法 3 的行 11-13 和行 17,bin(i) 中解的最大 g 值不会减小,因此 J_max 也不会减小。
这说明总是存在满足![]() 的
x ∈ bin(i)。
接下来考虑 J_max 增大,直到找到一个 f 值至少为
的
x ∈ bin(i)。
接下来考虑 J_max 增大,直到找到一个 f 值至少为![]() 的解。
令 x 表示有最大 g 值的解。
根据引理 1,翻转 x 的特定 0 位可以生成一个满足 |x'| = i + 1 的解 x',且
的解。
令 x 表示有最大 g 值的解。
根据引理 1,翻转 x 的特定 0 位可以生成一个满足 |x'| = i + 1 的解 x',且
![]()
其中,由于 J_max = i,根据![]() ,第一个不等式成立;
而根据 ∀r ∈ R : 1 − r ≤ e^−r,最后一个不等式也成立。
因此,可以得到
,第一个不等式成立;
而根据 ∀r ∈ R : 1 − r ≤ e^−r,最后一个不等式也成立。
因此,可以得到![]() 。
在每轮迭代中,x' 能以至少
。
在每轮迭代中,x' 能以至少![]() 的
概率生成,这说明在生成满足 |x'| = i + 1 和
的
概率生成,这说明在生成满足 |x'| = i + 1 和![]() 的 x' 之前的预期迭代数量至多为 enP_max。
然后,考虑 cˆ(x') 的两种情况:
(1)如果 cˆ(x') > B,则式 (8) 说明
的 x' 之前的预期迭代数量至多为 enP_max。
然后,考虑 cˆ(x') 的两种情况:
(1)如果 cˆ(x') > B,则式 (8) 说明![]() 。
令
。
令![]() ,
则有:
,
则有:
![]()
其中,根据定义 1,第一个不等式成立;
根据 α_f ∈ [0, 1],最后一个不等式成立。
在每轮迭代中,可通过选择 0^n 并翻转特定的 0 位来生成 y(以至少 1/enP_max 的概率发生)。
因此,在至多 enP_max 个预期迭代轮数中可以生成 y。
根据行 7-10 和 14-17 中 P 的更新流程,可以知道一旦生成了 y,P 总是包含一个满足 f(z) ≥ f(y) 的解 z ∈ bin(1)。
可以验证,总是存在一个满足 f(z') ≥ f(x) 的解 z' ∈ bin(i)。
根据算法 3 的行 22,最后返回的解会是 f 值最大的解。
因此,EAMC 输出的解的 f 值至少为:
![]()
(2)如果 cˆ(x') ≤ B,根据行 7-13 和 17 的更新流程,可知 x' 将被加入到 P 中,因为不存在满足 g(z) ≥ g(x') 的 z ∈ bin(i + 1);
否则 g(z) ≥ g(x') ≥ f(X˜),这与 J_max 的定义相矛盾。
现在,J_max = i + 1.
重复以上分析,EAMC 将输出满足![]() 的解 z,这意味着达到了所需的近似保证,或者 J_max 将继续增大,直到到达最大值 n。
后面的情况意味着 cˆ(1^n) ≤ B,而 EAMC 将输出 1^n;
因为 f 单调,所以这是最优的。
现在来看看预期的迭代总数。
要使 J_max ≥ 1,预期的迭代数量最大为 enP_max;
为了将 J_max 从 1 增大到 n,预期的迭代数量至多为 (n-1) · enP_max;
为了生成 y,预期的迭代数量至多为 enP_max。
因为 bin(i) 中最多有两个解,其中 1 ≤ i ≤ n – 1(算法 3 的行 17);
而 bin(0) 和 bin(n) 最多只有一个解,有 P_max ≤ 2n。
因此,预期的迭代总数至多为
的解 z,这意味着达到了所需的近似保证,或者 J_max 将继续增大,直到到达最大值 n。
后面的情况意味着 cˆ(1^n) ≤ B,而 EAMC 将输出 1^n;
因为 f 单调,所以这是最优的。
现在来看看预期的迭代总数。
要使 J_max ≥ 1,预期的迭代数量最大为 enP_max;
为了将 J_max 从 1 增大到 n,预期的迭代数量至多为 (n-1) · enP_max;
为了生成 y,预期的迭代数量至多为 enP_max。
因为 bin(i) 中最多有两个解,其中 1 ≤ i ≤ n – 1(算法 3 的行 17);
而 bin(0) 和 bin(n) 最多只有一个解,有 P_max ≤ 2n。
因此,预期的迭代总数至多为![]() 。
。
当对 α_f 的确切计算很困难时,在 α_f 上的下界(用 α 表示)可以用在替代目标 g 中,EAMC 能实现![]() 的近似比,如推论 1 所示。
在定理 3 的证明中,近似比中包含第一个 α_f 的因子(即
α_f/2)是从式(9)推导出来的,这不依赖于 g。
因此,这个因子会保持不变。
包含第二个 α_f 的因子(即
的近似比,如推论 1 所示。
在定理 3 的证明中,近似比中包含第一个 α_f 的因子(即
α_f/2)是从式(9)推导出来的,这不依赖于 g。
因此,这个因子会保持不变。
包含第二个 α_f 的因子(即![]() )是从式(8)推导的,这会应用于 g 的定义。
因为现在 α 被用在 g 中,这个因子中的 α_f 会相应地变为 α。
推论 1。
对于定义 3 中的问题,当在 α_f 上的下界(用 α 表示)应用于式(6)中的替代目标 g 上时,满足
)是从式(8)推导的,这会应用于 g 的定义。
因为现在 α 被用在 g 中,这个因子中的 α_f 会相应地变为 α。
推论 1。
对于定义 3 中的问题,当在 α_f 上的下界(用 α 表示)应用于式(6)中的替代目标 g 上时,满足![]() 的 EAMC 可找到一个子集 X ⊆ V,其满足条件
的 EAMC 可找到一个子集 X ⊆ V,其满足条件
![]()
![]()
图 1:有两种线性成本限制(出度和随机)的最大覆盖。覆盖的顶点数量:越大越好。
![]()
图 2:有两种线性成本限制(出度和随机)的影响力最大化。影响力传播度:越大越好。
![]()
✄------------------------------------------------
加入机器之心(全职记者 / 实习生):hr@jiqizhixin.com
投稿或寻求报道:content
@jiqizhixin.com
广告 & 商务合作:bd@jiqizhixin.com
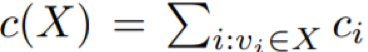 。
但在某些情况中,这个限制可能更加复杂,比如路径限制,这是单调非子模的。
举个例子,在移动机器人传感领域,需要计入在不同位置之间移动的成本以及在这些位置进行测量的成本。
用图 G = (V, E) 表示所有位置的路径网络,其中 c_e 表示穿过一条边 e ∈ E 的成本,c_v 表示访问一个节点 v ∈ V 的成本。
成本函数为
。
但在某些情况中,这个限制可能更加复杂,比如路径限制,这是单调非子模的。
举个例子,在移动机器人传感领域,需要计入在不同位置之间移动的成本以及在这些位置进行测量的成本。
用图 G = (V, E) 表示所有位置的路径网络,其中 c_e 表示穿过一条边 e ∈ E 的成本,c_v 表示访问一个节点 v ∈ V 的成本。
成本函数为 ,
其中
,
其中  是
访问 X 中每个节点至少一次的最短行走的成本,这通常是非子模的,而且无法在多项式时间中得到准确的计算。
本文的实验中,线性约束和路由约束都会用到。
是
访问 X 中每个节点至少一次的最短行走的成本,这通常是非子模的,而且无法在多项式时间中得到准确的计算。
本文的实验中,线性约束和路由约束都会用到。
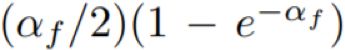 ,
但预期的运行时间是多项式的上限。
其证明依赖于引理 1,可以直观地看到,这意味着对于任意子集,某个特定项的包含都至少能将 f 提升一定量,这个量与离最佳结果的当前距离成比例。
这里假设 ∀v ∈ V : cˆ({v}) ≤ B;
因为在优化前可以将任意 cˆ({v}) > B 的 v 直接移除。
,
但预期的运行时间是多项式的上限。
其证明依赖于引理 1,可以直观地看到,这意味着对于任意子集,某个特定项的包含都至少能将 f 提升一定量,这个量与离最佳结果的当前距离成比例。
这里假设 ∀v ∈ V : cˆ({v}) ≤ B;
因为在优化前可以将任意 cˆ({v}) > B 的 v 直接移除。

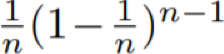

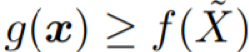 的
x ∈ bin(i)。
的
x ∈ bin(i)。
 的解。
令 x 表示有最大 g 值的解。
根据引理 1,翻转 x 的特定 0 位可以生成一个满足 |x'| = i + 1 的解 x',且
的解。
令 x 表示有最大 g 值的解。
根据引理 1,翻转 x 的特定 0 位可以生成一个满足 |x'| = i + 1 的解 x',且
 ,第一个不等式成立;
而根据 ∀r ∈ R : 1 − r ≤ e^−r,最后一个不等式也成立。
因此,可以得到
,第一个不等式成立;
而根据 ∀r ∈ R : 1 − r ≤ e^−r,最后一个不等式也成立。
因此,可以得到 。
在每轮迭代中,x' 能以至少
。
在每轮迭代中,x' 能以至少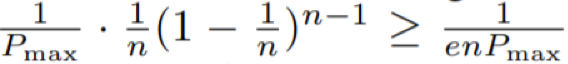 的
概率生成,这说明在生成满足 |x'| = i + 1 和
的
概率生成,这说明在生成满足 |x'| = i + 1 和 的 x' 之前的预期迭代数量至多为 enP_max。
然后,考虑 cˆ(x') 的两种情况:
的 x' 之前的预期迭代数量至多为 enP_max。
然后,考虑 cˆ(x') 的两种情况:
 。
令
。
令 ,
则有:
,
则有:
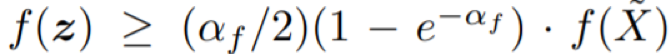 的解 z,这意味着达到了所需的近似保证,或者 J_max 将继续增大,直到到达最大值 n。
后面的情况意味着 cˆ(1^n) ≤ B,而 EAMC 将输出 1^n;
因为 f 单调,所以这是最优的。
的解 z,这意味着达到了所需的近似保证,或者 J_max 将继续增大,直到到达最大值 n。
后面的情况意味着 cˆ(1^n) ≤ B,而 EAMC 将输出 1^n;
因为 f 单调,所以这是最优的。
 。
。
 的近似比,如推论 1 所示。
在定理 3 的证明中,近似比中包含第一个 α_f 的因子(即
α_f/2)是从式(9)推导出来的,这不依赖于 g。
因此,这个因子会保持不变。
包含第二个 α_f 的因子(即
的近似比,如推论 1 所示。
在定理 3 的证明中,近似比中包含第一个 α_f 的因子(即
α_f/2)是从式(9)推导出来的,这不依赖于 g。
因此,这个因子会保持不变。
包含第二个 α_f 的因子(即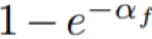 )是从式(8)推导的,这会应用于 g 的定义。
因为现在 α 被用在 g 中,这个因子中的 α_f 会相应地变为 α。
)是从式(8)推导的,这会应用于 g 的定义。
因为现在 α 被用在 g 中,这个因子中的 α_f 会相应地变为 α。
 的 EAMC 可找到一个子集 X ⊆ V,其满足条件
的 EAMC 可找到一个子集 X ⊆ V,其满足条件