变量选择

会员服务 ·

2017 年 12 月 7 日 Datartisan数据工匠

点击上方

Datartisan数据工匠

可以订阅哦！

主要内容

本章包括以下主题：

常规机器学习算法（预测或聚类）的最佳变量排名。
选择具有和不具有预测模型变量的规则。
变量在群体中的作用（直觉和信息理论）。
用R探索在实践中最好的变量子集。

选择最佳变量也称为特征选择，选择最重要的预测因子，选择最佳预测因子等。

图像：是神经网络吗？不。来自“千年模拟项目”的黑暗物质。

导言

选择最好的变量就像做一个故事的总结，我们要关注那些最能概括我们谈论内容的细节。我们要取得在关于不必要的细节谈论太多（过度拟合）和关于故事的本质谈论太少（拟合不足）两者之间的平衡。

另一个例子可能是购买新笔记本电脑的决定过程：我们最关心的是什么功能？价格，颜色和运输方式？颜色和电池寿命？还是只是价格？

从信息理论的角度来看，机器学习的关键点在于，我们正在研究的数据具有熵（混沌）。当我们选择变量时，我们正在通过添加信息来减少我们系统的熵。

什么是“最好的”选择？

这章说“最好”，但我们最好首先提出一个概念点，一般来说，没有唯一的最佳变量选择。

从这个观点出发是很重要的，因为在探索许多根据预测能力对变量进行排序的算法时，我们可以找到不同的和相似的结果。

比如：

算法1选择了最佳变量var_1，其次是var_5和var_14。
算法2做了这个排名：var_1，var_5和var_3。

我们可以假设，基于算法1，精度为80％，而基于算法2的精度为78％。考虑到每个模型都有内在的差异，结果可以看作是一样的。

这个观点可以帮助我们缩短追求完美变量选择的时间。

然而，在极端情况下，会有一组变量在许多算法中排名很高，对于那些没有预测能力的变量也是如此。经过几次运行，最可靠的变量将迅速出现，所以：

结论：如果结果不好，重点应该是改进和检查数据预处理步骤。下一节将举例说明。

深入变量排名

给一个特定指标的变量排名在文献和算法中是一个常见的单变量分析问题。

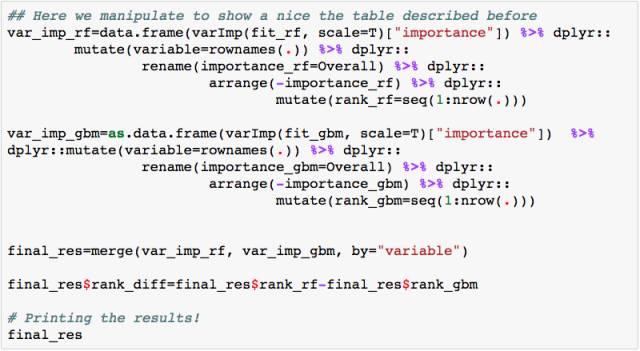
我们将创建两个模型：随机森林和梯度提升机（GBM），使用R包caret来对数据进行交叉验证。如下，我们将比较每个模型返回的最佳变量排名。

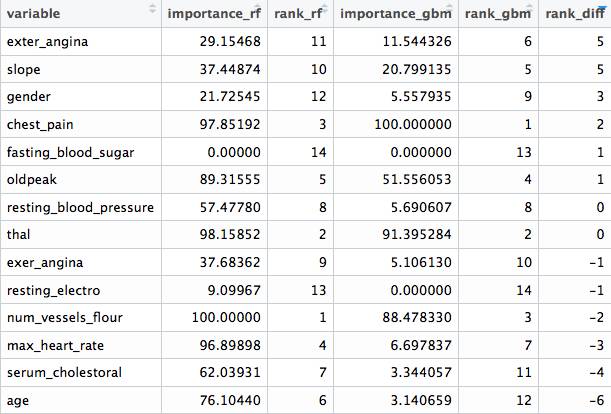
现在我们可以进行比较。 importance_rf和importance_gbm这两列代表着每个算法测量的权重。基于每个度量，有着代表权重序列的rank_rf和rank_gbm，最终rank_diff(rank_rf-rank_gbm) 代表每个算法对变量排序的不同。

可以看到有在两个模型(fasting_blood_sugar)中都不重要的变量。另有一些变量保持在权重的前列，比如chest_pain和thal.

根据该特定模型，不同的预测模型实现方式有自己判断什么是最佳特征的标准。这种不同算法的排名不同。有关内部重要性度量的更多信息，请参见caret documnetation

更重要的是，在诸如GBM和随机森林这样的基于树的模型中，有一个择取变量的随机组件，选择时的权重基于构建树时的先验和自动变量。每个变量的权重还依赖于其他因素，而不仅仅取决于其独立的贡献：变量在组中作用。我们将在稍后回到此部分内容。

虽然排名会因算法而异，但一般来说，我们之前提到的所有这些结果之间存在相关性。

结论：每个排名都不是“最后的真相” ，它给了我们信息的相对位置。

选择的规则

做变量选择有两种主要方法：

预测模型依赖：

像我们以前看到的那样，这是最常见的。该模型将根据一个精确度的内在度量来对变量进行排序。在树型模型中，诸如信息增益，基尼指数，节点杂质等指标。参考文献[4]，[5]。

非预测模型依赖：

有趣的是这些方法不像其他方法那样流行，但它们被证明在与基因组数据相关的领域表现非常出色。它们主要用于寻找与某些疾病相关的相关基因（输入变量），如癌症（目标变量）。

来自这个领域的数据的特点是拥有大量的变量（数千个），比其他领域的问题要大得多。

执行此操作的一种算法是mRMR ，最小冗余最大相关特征选择（Minimum Redundancy Maximum Relevance Feature Selection）的缩写。它在mRMRe包中有自己的R实现。

改进变量

变量可以通过对它们进行处理来增加预测能力。

这本书现在包括：

分类变量改进。
通过cross_plot函数合并变量，减少数值变量中的噪声。
为预测模型进行异常值预处理。
分析，缺失数据：预测建模的分析，处理和插补。

还有更多即将推出……

依据专业领域知识进行清理

它与算法程序无关，而是与数据所属的领域有关。

想象一下来自调查的数据。这次调查有一年的历史，前三个月没有良好的过程控制。插入数据时，用户可以输入任何想要的内容。这段期间的变量可能是虚假的。

如果数据在给定的时间段内变量为空，为零或极端值时，那么会很容易识别。

我们应该问自己一个问题：

这个数据是否可靠？请记住，预测模型将像一个孩子一样学习，它不会判断数据，只是从中学习。如果数据在给定的时间内是虚假的，那么我们应该删除这些输入。

在这一点上更进一步，我们应该进行更深入的探索性数据分析。不管是从数字上还是图形上。

变量集体发挥作用

在选择最佳变量时，主要目的是获取那些携带关于目标、结果和因变量的信息最多的变量。

预测模型将根据其从1到'N'的输入变量找到其权重或参数。

在解释事件时变量通常不是孤立工作的。引用亚里士多德的话：

“The whole is greater than the sum of its parts.”

在选择最佳特征时同样如此：

使用两个变量构建预测模型可能会比仅使用单变量构建的模型具有更高的精度。

例如：构建基于变量var_1的模型可以导致总体准确度达到60％。另一方面，构建基于var_2的模型可以达到72％的精度。但是当我们组合var_1和var_2这两个变量时，我们可以达到80％以上的精度。

R中的示例：集体发挥作用的变量

以下代码可以作为例子说明亚里士多德在多年前说的话：

模型1基于输入变量max_heart_rate

模型2基于输入变量chest_pain

模型3基于输入变量max_heart_rate和chest_pain每个模型返回指标ROC，结果要同时考虑两个变量做出的改进，而不是将每个变量隔离。

一个小例子（基于信息理论）

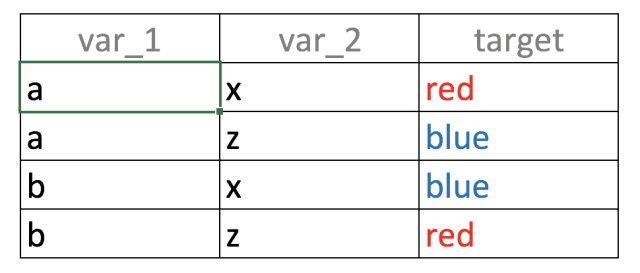
考虑以下大型数据表，有4行，2个输入变量（var_1，var_2）和一个结果（target）：

如果我们只建立一个基于var_1的预测模型，会发现什么？ a的值与输出变量blue和red以相同的比例相关（50％）：

如果var_1='a'则target ='red'的可能性为50％（第1行）

如果var_1='b'则target ='blue'的可能性为50％（第2行）

对var_2会得到同样的分析结果。

当相同的输入与不同的结果相关时，它被定义为噪声。就和一个人告诉我们： “明天会下雨的！“另一个说： ”明天肯定不会下雨“ 是一样的。

我们会想... “OMG！我需要伞吗？“ 😱

回到这个例子，同时拿两个变量，输入和输出之间一一对应：”如果var_1='a'而且var_2='x'那么target='red'是100％”。您也可以尝试其他组合。

总结：

这是变量集体发挥作用的一个例子，同时考虑到var_1和var_2时预测能力提升了。

尽管如此，考虑到最后的分析，会引出一个更加深入的话题。如果每列都规定Id（每个值都是独一无二的）来预测会怎样？输入输出之间是一一对应的...但它是一个有用的模型吗？本书将会用更多信息理论的知识进一步说明。

结论

基于heart_disease数据做出的R语言示例显示在考虑两个变量时预测成功率平均提高了9％而不是太差。😉这个改进的百分比是变量分组工作的成果。
在变量包含信息（如maxheartrate和chestpain （或var1和var_2 ））的情况下，会显出效果。
将噪声变量放在良好变量旁边通常会影响整体性能。
如果输入变量之间不相关，则在同组中工作效果更好。这在实践中难以优化。在下一节会有进一步说明...

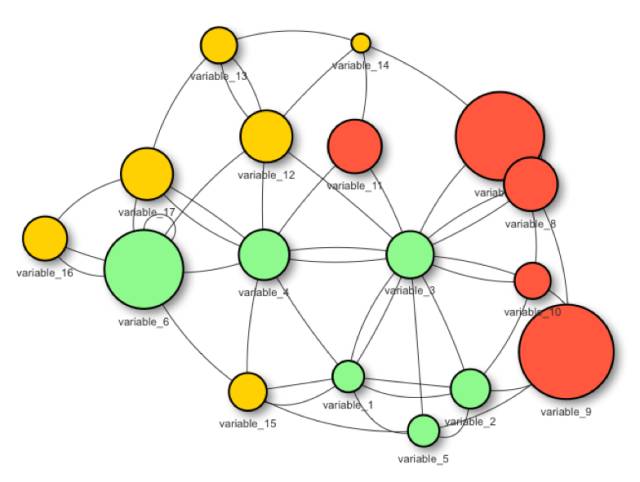
输入变量之间的相关性

理想的情况是建立一个预测模型，只有它们之间不相关的变量。在实践中，为所有变量保持这种情况是很难的。

通常会有一组变量在它们之间不相关，但也有其他一些变量至少有一些相关性。

在实践中一个合适的解决方案要排除强相关性的变量。

关于如何衡量相关性，对于线性或非线性程序，结果可能会有很大差异。

添加相关变量有什么问题？

问题是我们增加了模型的复杂性：它通常更耗时，更难理解，更难解释，更不准确等。这是我们在减少分类变量中的基数方面的一个作用。

一般规则是：尝试添加与输出相关但不相关的前N个变量。这将在下一节说明。

保持简洁

自然以最简短的方式运作。 - 亚里士多德。

奥卡姆剃刀法则：在多个假设中，应该选择最简单的假设。

重新用机器学习来解释这个句子，那些“假设”可以看作是变量，所以我们有：

在不同的预测模型中，应该选择最少的变量。

当然，还有增减变量和模型的准确性的权衡。

具有大量变量的预测模型往往会过度拟合。而另一方面，具有低数量变量的模型将导致拟合不足。

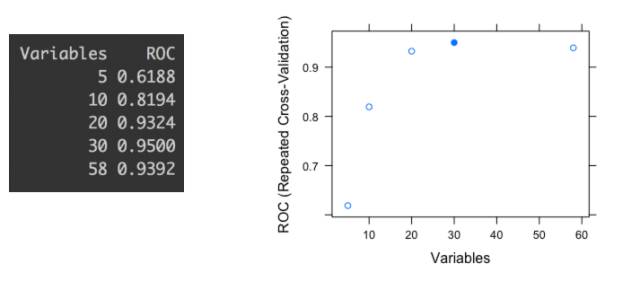
高和低的概念对于被分析的数据来说是高度主观的。实际上，我们可能会有一些精度指标，例如ROC值。如下图所示：

最后一幅图显示了不同的变量子集（5,10,20,30和58）的ROC精度指标。每个点表示给定一定数量的用于构建模型的变量的ROC值。

我们可以检查当模型用30个变量构建时最高的ROC。如果我们仅基于自动化流程做选择，那么我们可能会选择一个倾向于过拟合的子集。该报告由R（参考[2]）中的caret库产生，但在其他软件中也是类似。

仔细观察子集元素数为20和30之间的差异;只有1.8％的改善 - 从0.9324到0.95-选择10个变量。换句话说：选择50％以上的变量会影响不到2％的改进。

甚至更进一步，这个2％可能是一个误差幅度，由每个预测模型的预测变量而产生。

结论:

在这种情况下，根据奥卡姆的剃刀原理，最好的解决方案是用20个变量的子集构建模型。

可以尝试向别人解释 - 并且理解 - 具有20个变量的模型比有30个变量的类似模型更好。

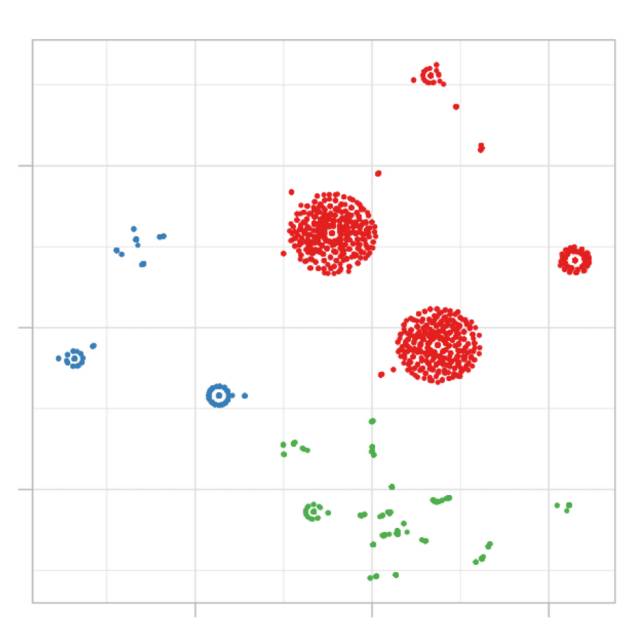
聚类中的变量选择？

这个概念通常只出现在预测建模中，即有一些变量来预测目标。在聚类中，没有目标变量，我们让数据说话，而自然分割根据一些距离度量而出现。

然而，并不是每一个变量都用同样的方式对集群模型的不同之处作出贡献。简而言之，如果我们有3个聚类作为产出，并且测量每个变量的平均值，我们会预期这些平均值在它们之间是相当不同的，不是吗？

建立2个聚类模型，在第一个模型中age变量的平均值为24,33和26年;而在第二个模型中，我们有：23,31和46。在第二个模型中，变量age变化较大，因此与模型更相关。

这只是考虑两个模型的一个例子，但是只考虑一个模型时也是一样的。那些跨越均值距离更大的变量往往会比其他变量更好地定义聚类。

与预测建模不同，在聚类中不太重要的变量不应该被去除，那些变量在该特定模型中并不重要，但是如果我们用其他参数构建另外一个变量，那么它们可能是重要的。集群模型的质量非常主观。

最后，我们可以运行一个随机森林模型，将该集群作为目标变量，以这种方式快速收集最重要的变量。

实践中选择最佳变量

简短的答案

从你使用的算法中获取前N个变量，然后使用此子集重新构建模型。不是每个预测模型都会检索变量排名，但如果是，则使用相同的模型（例如梯度增强机）来获得排名并构建最终模型。

对于那些没有内置选择最佳特征程序的k-最近邻的模型，使用其他算法进行选择是有效的。这将产生比使用所有变量更好的结果。

长的答案

如果可能的话，无论是前N个还是最后的M个变量，请与知道上下文，业务或数据源的人员对列表进行验证。至于这些不良变量，我们可能会在处理变量的时候有遗漏从而对其预测能力产生破坏。
了解每个变量，及其在上下文中的意义（商业，医疗，其他）。
进行探索性数据分析以查看被作为目标变量的最重要变量分布，以及选择是否有意义？如果目标有两个选择，则可以使用函数cross_plot。
变量的平均值是否随时间而显着变化？检查分布的突然变化。
怀疑基的数量排名最高的变量（如邮政编码，可以说超过+100类）。预测模型中的高基数变量可以查看的更多信息。[3]
当进行选择时，也可以作为预测模型，尝试使用包含重新抽样机制（如bootstrapping）的方法和交叉验证。
尝试其他方法来查找变量组，比如之前提到的变量：mRMR。
如果选择不符合要求，请尝试创建新变量，可以查看数据预处理章节。