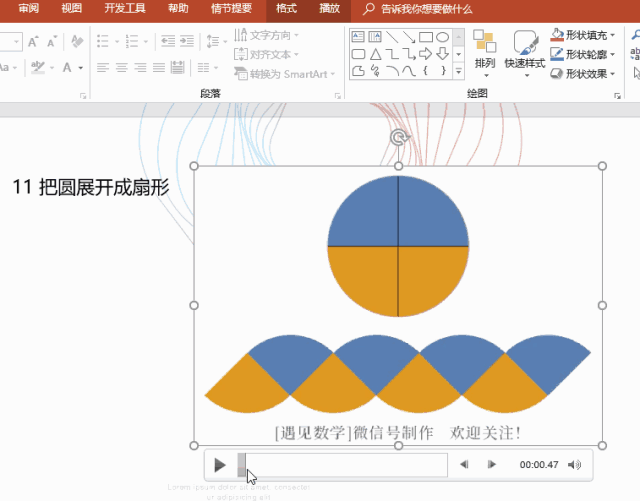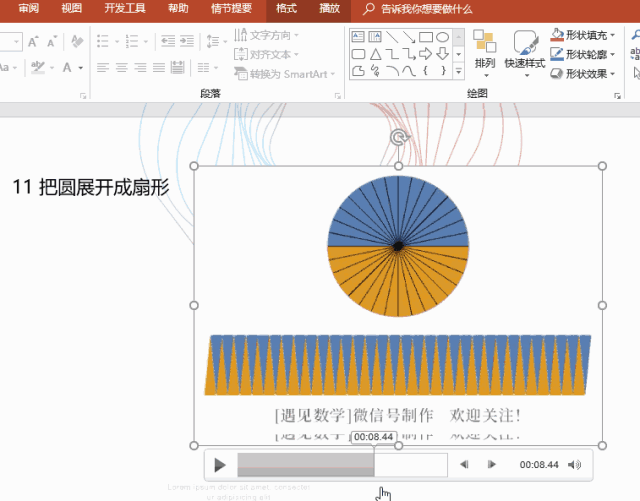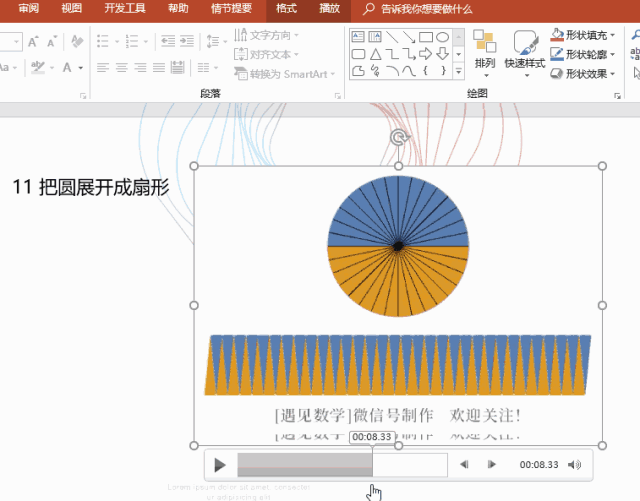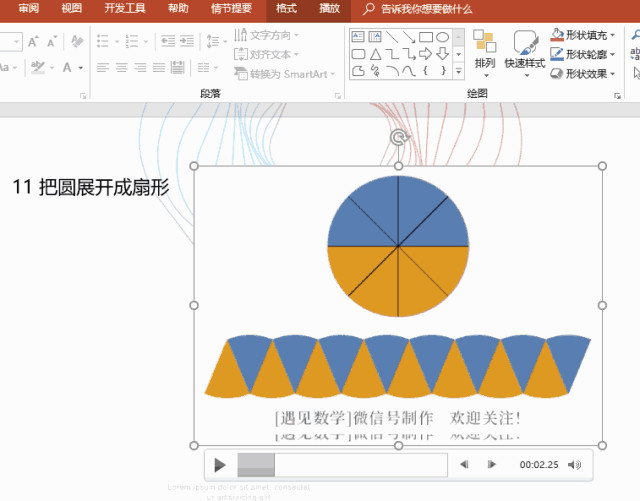
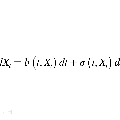微积分的本质在于近似与忽略 - 简单微积分

虽然整体计算很难,但分成较小的部分就会变成简单的累加。这就是微积分厉害之处
下文节选自《简单微积分》, 已获人邮图灵授权许可, [遇见数学] 特此表示感谢!
微积分的真身
微分相关的冒险
不少人会误解“世界中尽是可微函数”。有时在微积分的书里也可以看到这样的表述。
例如,“股价变动的图像可以微分,所以就可以知道未来股价的上下浮动”,如果你读到这样的表述,千万不可相信。


一般讨论股价会使用概率建立模型。最简单的是使用随机摆动的点,即假设股价是随机摆动的。
根据详细的研究可知,这种点的轨迹在任何时候都是锯齿状的(不可微),和上一次的魏尔斯特拉斯函数相似。即,可以证明在点的随机摆动轨迹中,几乎所有的点处都没有切线。股价变动并不是可以用普通微分去预测的温顺之物。在和概率现象纠缠不休的函数中,会频繁出现不可微函数。
图 126 是日经平均股价的图像。锯齿状的线是实际股价,在顺滑的线中,13 周移动平均线是平均了 13 周的股价,26 周移动平均线同样是平均了过去 26 周的股价。在《股价可以预测》这本书中, 恐怕把这条“移动平均线”类的东西作为研究图像了。
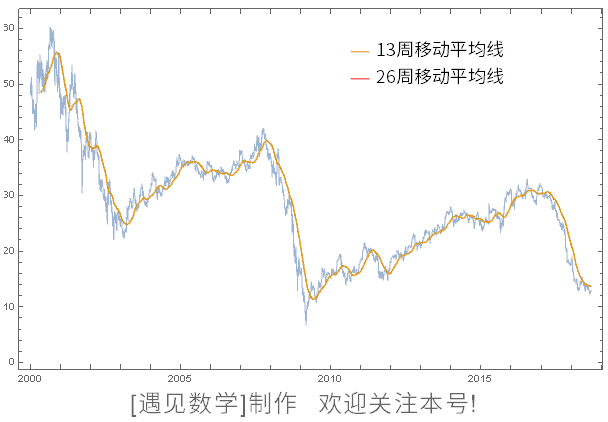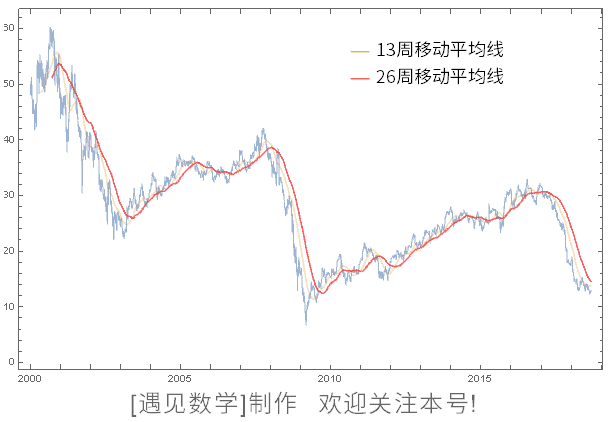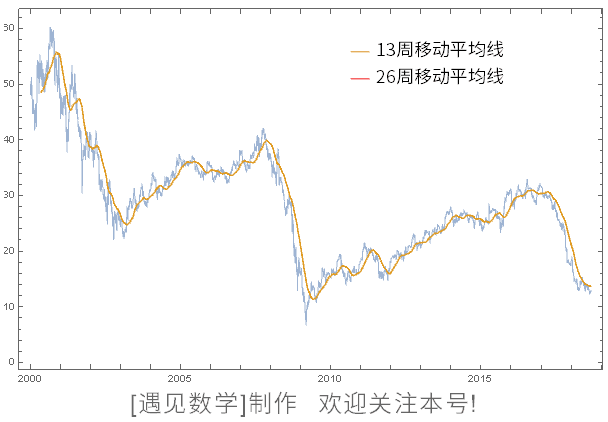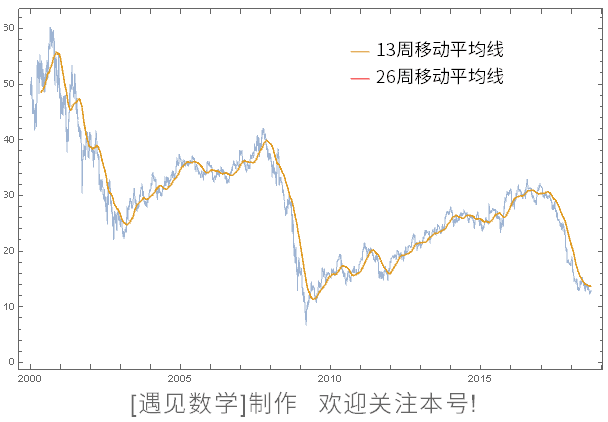
图126 [遇见数学]重新制作了动画, 修改为谷歌平均股价(2000年1月~至今), 书中为日经平均股价数据
移动平均线是低通滤波器(Low Pass Filter)的一种,会移除锯齿状的部分(高频率),只让顺滑的部分(低频率)通过。以声音为例,孩子的声音多是高频率,大叔的声音多是低频率。所以, 如果让孩子的声音通过低通滤波器(Low Pass Filter),孩子的声音就会变得像大叔的声音。
在了解股价“大致波动”的时候,因为锯齿状的部分很碍事,所以应该使用移动平均线。
但是,原本的股价“本质上”就是锯齿状的(图 126 的实线)。想要微分这种任何地方都不可微分的内容,不得不说是错误的。
但是,要说股价预测和微积分完全没有关系的话,也并非如此。这种概率模型叫作随机微分方程,使用某种微积分是可以进行解析的。
虽说如此,但这和通常的微积分相当不一样,是一门独特的数学[23]。当然,即使使用随机微分方程式,也无法去预测股价。
[23] 名称虽然是随机微分方程式, 但是实际上是积分方程式, 而且这种积分也 不是本书中出现的规规矩矩的积分.
微积分的应用虽然不具有预测股价这类功能,但是微积分在现实社会中的作用巨大。可以说,微积分是所有学问的基础,反而很难具体说“微积分在这里起作用”,就像空气和水一样。
近似和忽略
正如前文所述,微积分的本质在于近似与忽略。近似指的是忽略一些东西,只给出大概的答案。
但是,在学校的数学教学中,当被问到“平方后等于 2 的值是多少”时,不能回答“大概是 1.4”,原则上必须回答“是 √2 ”。微积分的本质内容“近似与忽略”可不能被理解成这类方法。
即使是复杂的形状,也可以将其视为简单长方形的组合(积分),函数在局部可以视为切线或者抛物线(微分),这个思考角度才是微积分的要领。
重要的是不要在意细节。不在意细小的部分,“用直线段近似函数图像”就可以搞清楚容积最大的冰激凌蛋卷筒是什么形状,也可以“把曲线看作折线的组合”来计算悬链线的长度。虽然整体计算很难,但分成较小的部分就会变成简单的累加。这就是微积分厉害之处。
实际上,这种思想并不仅限于微积分,可以说整个数学都是这样的。微积分则是了解该方法有效性的最好素材。
实际上,我们居住的现实世界中,近似可以说是无处不在。比如,不存在无限小的东西(无法比基本粒子更小),宇宙也并非无限广阔。
但是,在实际的微积分中,要考虑无限小的量,或者无限大的空间,这是近似。忽略基本粒子的大小,搁置宇宙的边界限制,这种想法或许与事实相悖,但是这种方法给我们带来的恩惠却不可估量。
微分积分的内容是从细致分割图形开始讲起的,之后又讲到自然常数e,最后又到悬链线的长度。读到这里,大家是不是已经自然而然地认可“近似和忽略”的思考方法呢?如果是的话,那么这就是很大的进步了。(本书完)
☟ 点击【阅读原文】进一步查看或购买此书