时间信息编码为机器学习模型特征的三种方法（附链接）

大数据文摘授权转载自数据派THU

作者：Eryk Lewinson

翻译：张睿毅

校对：张睿毅

设置与数据

在本文中，我们主要使用非常知名的Python包，以及依赖于一个相对不为人知的scikit-lego包，这是一个包含许多有用功能的库，这些功能正在扩展scikit-learn的功能。我们导入所需的库，如下所示：

import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as snsfrom datetime import datefrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import FunctionTransformerfrom sklearn.metrics import mean_absolute_errorfrom sklego.preprocessing import RepeatingBasisFunction

为了简单起见，我们使用自生成数据。在此示例中，我们使用人工时间序列。我们首先创建一个空的数据帧，其索引跨越四个日历年（我们使用pd.date_range）。然后，我们创建两列：

• day_nr – 表示时间流逝的数字索引

• day_of_year – 一年中的第一天

最后，我们必须创建时间序列本身。为此，我们将两条变换的正弦曲线和一些随机噪声结合起来。用于生成数据的代码基于scikit-lego文档中包含的代码。

# 避免重复np.random.seed(42)
# 生成日期的数据格式range_of_dates = pd.date_range(start="2017-01-01",                           End="2020-12-30")X = pd.DataFrame(index=range_of_dates)
# 创建日期数据的序列X["day_nr"] = range(len(X))X["day_of_year"] = X.index.day_of_year
# 生成目标成分signal_1 = 3 + 4 * np.sin(X["day_nr"] / 365 * 2 * np.pi)signal_2 = 3 * np.sin(X["day_nr"] / 365 * 4 * np.pi + 365/2)noise = np.random.normal(0, 0.85, len(X))
# 合并获取目标序列y = signal_1 + signal_2 + noise
# 画图y.plot(figsize=(16,4), title="Generated time series");

图 1：生成的时间序列。

然后，我们创建一个新的 DataFrame，在其中存储生成的时间序列。此数据帧将用于比较使用不同特征工程方法的模型性能。

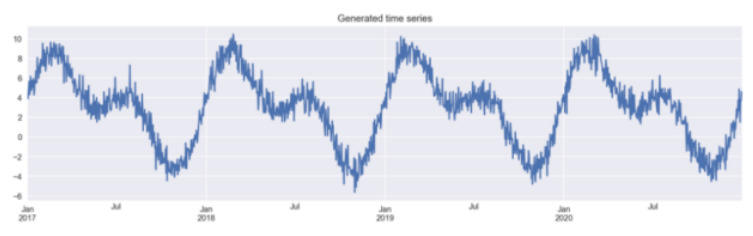
results_df = y.to_frame()results_df.columns = ["actuals "]

创建与时间相关的要素

在本节中，我们将介绍生成时间相关特征的三种老练方法。

在我们深入研究之前，我们应该定义一个评估框架。我们的模拟数据包含四年的观察结果。我们将使用生成的前 3 年的数据作为训练集，并将在第4年进行评估。我们将使用平均绝对误差 （MAE） 作为评估指标。

下面我们定义一个变量，该变量将用于分割两个集合：

TRAIN_END = 3 * 365

方法1：虚拟变量

我们从您很可能已经熟悉的东西开始，至少在某种程度上是这样。对时间相关信息进行编码的最简单方法是使用虚拟变量（也称为单热编码）。

让我们看一个示例。

X_1 = pd.DataFrame(data=pd.get_dummies(X.index.month, drop_first=True, prefix="month"))

在下面，您可以看到我们操作的输出。

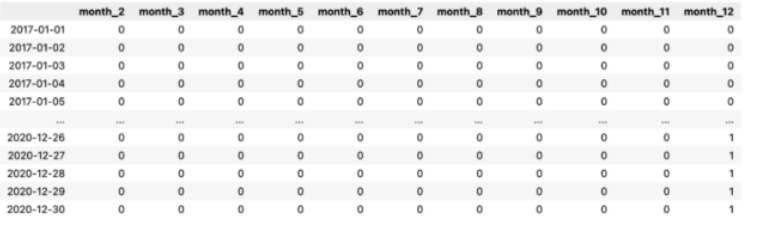
表 1：带有月份假人的数据帧。

首先，我们从 DatetimeIndex 中提取有关月份的信息（编码为 1 到 12 范围内的整数）。然后，我们使用pd.get_dummies函数来创建虚拟变量。每列都包含有关观测值（行）是否来自给定月份的信息。

您可能已经注意到，我们已经降低了一个级别，现在只有11列。我们这样做是为了避免在使用线性模型时可能出现的臭名昭著的虚拟变量陷阱（完美的多重共线性）问题。

在我们的示例中，我们使用虚拟变量方法来获取观测值的月份。其实也可以使用相同的方法获取来自 DatetimeIndex 的一系列其他信息。例如，一年中的日/周/季度，给定一天是否为周末的标志，一个周期的第一天/最后一天等等。可以找到一个列表，其中包含所有可能的从pandas文档索引中提取的功能，可在 pandas.pydata.org找到。

额外提示：以下已经不属于简单练习的范围了，但在现实生活中，我们还可以使用有关特殊日子的信息（想想国定假日，圣诞节，黑色星期五等）来创建功能。holidays是一个不错的Python库，包含每个国家/地区特殊日子的信息，无论过去和未来。

如简介中所述，特征工程的目标是将复杂性从模型转移到特征集。这就是为什么我们将使用最简单的ML模型之一 -线性回归 – 展示一下拟合时间序列的程度，在我们仅使用创建的虚拟数据下。

model_1 = LinearRegression（）.fit（X_1.iloc[：TRAIN_END]， y.iloc[：TRAIN_END]）
results_df["模型_1"] = model_1.predict（X_1）results_df[["actuals"，"model_1"]].plot（figsize=（16，4），title="用月虚拟变量拟合"）plt.axvline（date（2020， 1， 1）， c="m"， linestyle="--"）;

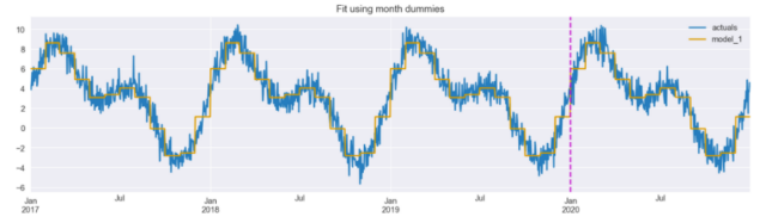
图 2：使用月份假人进行拟合。垂直线将训练集和测试集分开。

我们可以看到，拟合线已经很好地遵循了时间序列，尽管它有点锯齿状（类似阶梯） - 这是由虚拟特征的不连续性引起的。因此我们将尝试通过接下来的两种方法解决此问题。

但在继续之前，值得一提的是，当使用非线性模型（例如决策树（或其集合））时，别将诸如月份，或一年中的某天等特征显式编码设为随机数。这些模型能够学习序数输入特征与目标之间的非单调关系。

方法#2：具有正弦/余弦变换的循环编码

正如我们前面所看到的，拟合的线类似于步骤。这是因为每项虚拟数据都是单独处理的，没有连续性。然而，例如时间等变量存在明显的周期连续性。这意味着什么呢？

想象一下，我们正在处理购买者的数据。当我们纳入观察到的购买者消费月份的信息时，如果连续两个月之间存在更强的联系，是有道理的。按照这个逻辑，12月和1月之间以及1月和2月之间的联系很强。相比之下，1月和7月之间的联系就并不那么紧密。这道理同样适用于其他与时间相关的信息。

那么，我们如何将这些知识融入特征工程中呢？三角函数啊。我们可以使用以下正弦/余弦变换将循环时间特征编码为两个特征。

def sin_transformer(period):return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))

在下面的代码片段中，我们复制初始 DataFrame，添加带有月份数字的列，然后  使用正弦/余弦变换对月份和day_of_year两项进行编码。然后，我们绘制两对曲线。

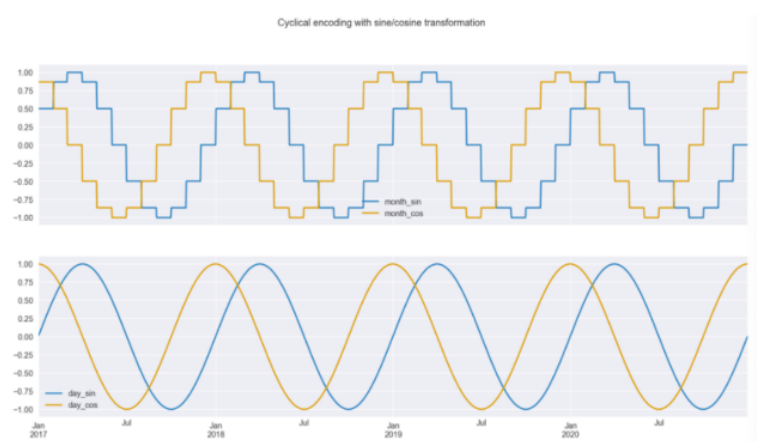
X_2 = X.copy()X_2["月"] = X_2.index.month
X_2["月_sin"] = sin_transformer(12).fit_transform(X_2)[" 月"]X_2["月_cos"] = cos_transformer(12).fit_transform(X_2)[" 月"]
X_2["日_sin"] = sin_transformer(365).fit_transform(X_2)["每年的日"]X_2["日_cos"] = cos_transformer(365).fit_transform(X_2)[" 每年的日"]
fig, ax = plt.subplots(2, 1, sharex=True, figsize=(16,8))X_2[["月_sin", "月_cos"]].plot(ax=ax[0])X_2[["日_sin", "日_cos"]].plot(ax=ax[1])plt.suptitle("用正余弦变换循环编码");

图 3：基于每月和每日频率的正弦/余弦变换。

如图 3 所示，我们可以从转换后的数据中得出两个知识。首先，我们可以很容易地看到，当使用月份进行编码时，曲线是阶跃的，但是当使用每日频率时，曲线要平滑得多；其次，我们也可以理解为什么我们必须使用两条曲线而不是一条曲线。由于曲线的重复性，如果在绘图中绘制一条单年水平直线，则会在两个地方穿过曲线。这还不足以让模型了解观测值的时间点。但是有了这两条曲线，就没有这样的问题，用户可以识别出每一个时间点。让大家看得更明白点，我们在散点图上绘制正弦/余弦函数的值。在图 4 中，我们可以看到一个圆的模式，没有重叠。

图 4：正弦和余弦变换的散点图。

让我们仅使用来自每日频率的新创建要素来拟合相同的线性回归模型。

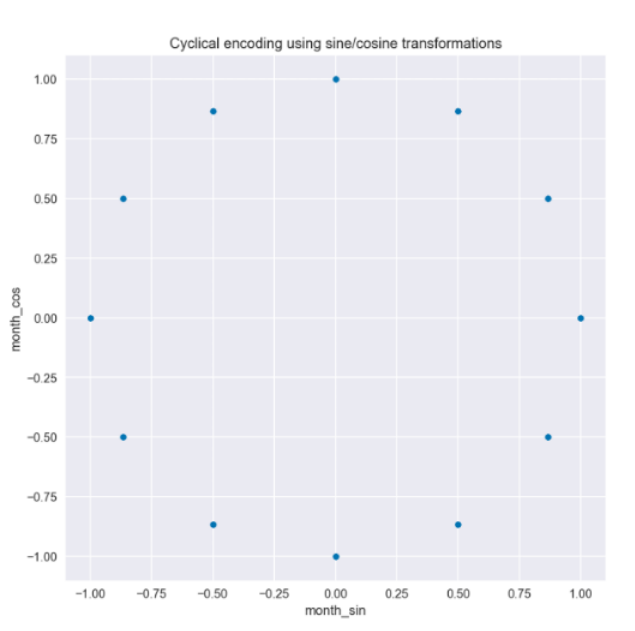
X_2_daily = X_2[["day_sin", "day_cos"]]model_2 = LinearRegression().fit(X_2_daily.iloc[:TRAIN_END],y.iloc[:TRAIN_END])results_df["model_2"] = model_2.predict(X_2_daily)results_df[["actuals", "model_2"]].plot(figsize=(16,4), title="使用正弦/余弦特征拟合")plt.axvline(date(2020, 1, 1), c="m", linestyle="--");

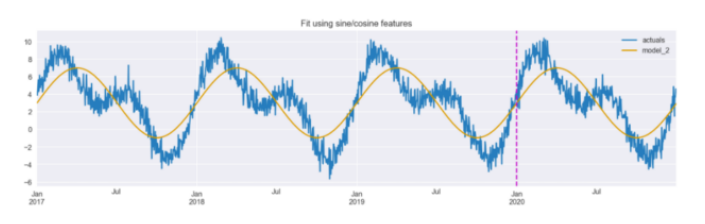
图 5：使用正弦/余弦变换拟合。垂直线将训练集和测试集分开。

图 5 显示，该模型能够拾取数据的总体趋势，识别具有较高和较低的周期。但是，预测的幅度似乎不太准确，乍一看，这种拟合似乎比使用第一种方法，虚拟变量，实现的拟合更差（图 2）。

在我们讨论第三种特征工程技术之前，值得一提的是，这种方法存在一个严重的缺点，尤其会在使用基于树的模型时，缺点很明显。最初设计，基于树的模型就是基于当时的单个特征进行拆分。正如我们之前提到的，正弦/余弦特征应该同时考虑，以便正确识别一段时间内的时间点。

方法#3：径向基函数

最后一种方法使用径向基函数。我们不会详细介绍它们的实际情况，但您可以在此处阅读有关该主题的更多信息。从本质上讲，我们再次希望解决第一种方法遇到的问题，即我们的时间特征具有连续性。

我们使用方便的scikit-lego库，它提供了RepeatmentBasisFunction类，并指定了以下参数：

• 我们要创建的基函数的数量（我们选择：12个）。

• 用于为 径向基函数（RBF）编制索引的列。我们这里采用的列是，该观测值来自一年中的哪一天。

• 输入范围 – 我们这里，范围是从1到365。

• 如何处理数据帧的其余列，我们将使用这些数据帧来拟合估计器。"drop"将仅保留创建的 RBF 功能，"passthrough "将保留旧功能和新功能。

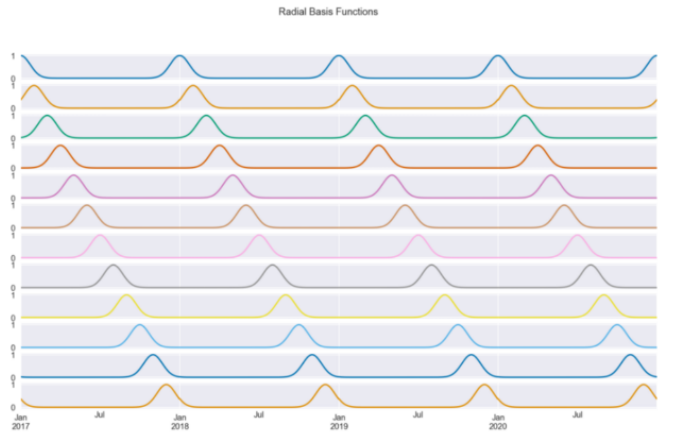
rbf = RepeatingBasisFunction(n_periods=12,                         column="day_of_year",                         input_range=(1,365),                         remainder="drop")rbf.fit(X)X_3 = pd.DataFrame(index=X.index,               data=rbf.transform(X))
X_3.plot(subplots=True, figsize=(14, 8),     sharex=True, title="Radial Basis Functions",     legend=False);

图 6：12 个径向基函数。

图 6 展示，我们使用日数作为输入，创建了 12 个径向基函数。每条曲线都包含有关多靠近本年某一天的信息（在选择此列的情况下）。例如，第一条曲线测量从1月1日开始的距离，因此它在每年的第一天达到峰值，在之后和当初升高的幅度对称地减小。

根据设计，基函数在输入范围内的间距相等。我们选择了12，因为我们希望RBF类似于月份。这样，每个函数都会显示到月份第一天的距离（由于月份的长度不相等）。

与前面的方法类似，让我们使用 12 个RBF 特征去拟合线性回归模型。

model_3 = LinearRegression().fit(X_3.iloc[:TRAIN_END], y.iloc[:TRAIN_END])
results_df["model_3"] = model_3.predict(X_3)results_df[["actuals", "model_3"]].plot(figsize=(16,4), title="使用RBF特征拟合")plt.axvline(date(2020, 1, 1), c="m", linestyle="--");

图 7：使用径向基函数拟合。垂直线将训练集和测试集分开。

图 7 显示，当使用 RBF 功能时，该模型能够准确地捕获真实数据。

使用径向基函数时，我们可以调整两个关键参数：

• 径向基函数的数目，

• 钟形曲线的形状 – 可以使用 RepeatingBasis 函数的宽度参数对其进行修改。

调整这些参数值的一种方法是使用网格搜索来确定给定数据集的最佳值。

最终比较

我们可以执行以下代码段，以生成编码时间相关信息的不同方法的数字比较。

results_df.plot(title="对比不同时间特征的拟合",figsize=(16,4), color = ["c", "k", "b", "r"])plt.axvline(date(2020, 1, 1), c="m", linestyle="--");

图 8：使用基于不同时间特征获得的模型，比较拟合。垂直线分开的是训练集和测试集

图 8 表明，径向基函数与所考虑的方法最接近。正弦/余弦特征允许模型拾取主要模式，但不足以完全捕获系列的动态。

使用下面的代码段，我们计算每个模型在训练集和测试集上的平均绝对误差。我们预计训练集和测试集的分数之间非常相似，因为生成的序列几乎完全是周期性的 - 年份之间的唯一区别是随机分量。

当然，在现实生活中情况并非如此，在现实中，随着时间的推移，我们会在同一时期之间遇到更多的变化。但是，在这种情况下，我们还会使用许多其他特征（例如趋势，或时间流逝的某种度量）来解释这些变化。

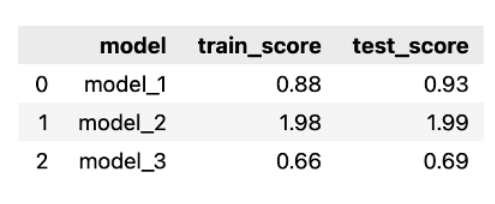
score_list = []for fit_col in ["model_1", "model_2", "model_3"]:scores = {    "model": fit_col,    "train_score": mean_absolute_error(        results_df.iloc[:TRAIN_END]["actuals"],        results_df.iloc[:TRAIN_END][fit_col]    ),    "test_score": mean_absolute_error(        results_df.iloc[TRAIN_END:]["actuals"],        results_df.iloc[TRAIN_END:][fit_col]    )}score_list.append(scores)
scores_df = pd.DataFrame(score_list)scores_df

与之前一样，我们可以看到使用RBF特征的模型产生了最佳拟合，而正弦/余弦特征的表现最差。我们对训练集和测试集所得分数之间的相似性假设也得到了证实。

表 2：训练/测试集的分数 （MAE） 比较。

总结

• 我们展示了三种将时间相关信息编码为机器学习模型特征的方法。

• 除了最流行的虚拟编码之外，还有一些方法更适合编码时间的循环性质。

• 使用这些方法时，时间间隔的粒度对于新创建的要素的形状非常重要。

• 使用径向基函数，我们可以决定要使用的函数的数量，以及钟形曲线的宽度。

您可以在我的GitHub上找到本文中使用的代码。如果您有任何反馈，我很乐意在Twitter上讨论。

引用：

[1] 时间相关的特征工程

https://scikit-learn.org/stable/auto_examples/applications/plot_cyclical_feature_engineering.html

[2] 预处理

https://scikit-lego.readthedocs.io/en/latest/preprocessing.html

[3] 时间/日期因素

https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#time-date-components

点「在看」的人都变好看了哦！