ICLR 2020 | 反事实因果理论如何帮助深度学习？

2020 年 4 月 29 日 学术头条

以深度学习为代表的表示机器学习取得了巨大的成功，尤其是在特征提取的能力方面。但是与此同时，一个巨大的问题是深度神经网络的黑箱问题和不稳定性问题。其中的一个根本原因，是基于相关性的统计模型容易学习到数据中的“伪关系(spurious relation)”，而非因果关系，从而降低了泛化能力和对抗攻击的能力。

一个潜在的方向，就是采用从 90 年代以来以 Judea Pearl 为代表的研究者们提出的因果推断理论来改进现有的表示学习技术。然而，因果分析框架和表示学习并非天生相容。因果分析通常是基于抽象的、高层次的统计特征来构建结构因果图；而表示学习则基于海量数据提取具体的、低层次的表示特征来辅助下游任务。为了结合这两者，MILA 的 Yoshua Bengio 提出了 System 2 框架，Max Planck Institute 的 Bernhard Schölkopf 提出的因果表示学习框架。这两者实际上的思考是一致的。

在本文中，我们将会讨论 ICLR 2020 上因果表示学习的 2 项有代表性的工作：如何利用因果理论中的反事实（counterfactual）框架来提高算法的稳定性和可解释性。

Learning the Difference That Makes A Difference with Counterfactually-Augmented Data

近年来，深度学习在自然语言处理领域获得了巨大的成功。但是，质疑声也一直不绝于耳，尤其是关于深度学习容易学习到语言数据集上的伪关系（spurious relation）的问题一直没有得到解决。因果推断理论告诉我们，这是由于混杂因子（confounding）造成的。

然而，将因果推断方法应用到自然语言处理面临着巨大的困难：什么是自然语言当中的随机变量？如何从表示中找出混杂因子？如何让学习结果更加稳定，避免受训练集中的伪关系影响？其中最大的困难，在于如何定义自然语言中的因果关系。

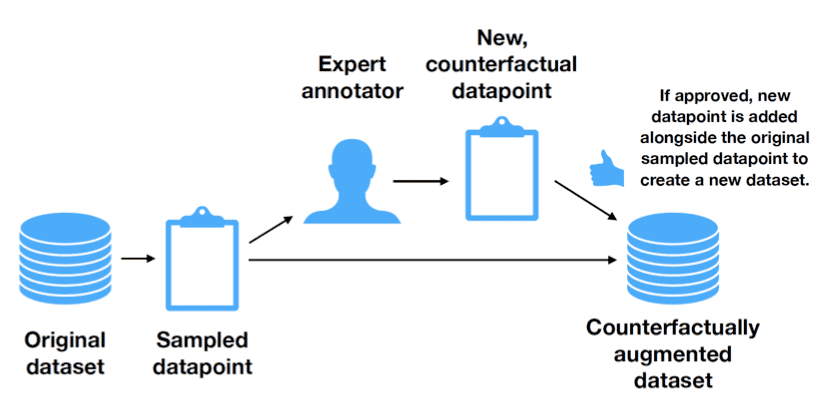
在本文中，作者设计了一种巧妙的方法，绕开了随机变量的定义问题，转而采用因果理论中的另一个重要概念——反事实——来进行 human in the loop 的数据增强以避免伪关系的干扰。

本文在情感分析的一个 3 分类数据集上，利用 Amazon’s Mechanical Turk 众包平台，要求人类对句子做轻微的修改。这些修改包括：

* 将事实变为希望：比如加入 supposed to be 表示虚拟语气

* 反讽语气：如加入引号修饰、改为反问句表示反讽

* 插入/替换修饰词：将 interesting 替换为 boring

* 插入短语，修改评分等

使评论的情感分类发生变化（如从正面变为负面）来进行数据增强。实验证明，对于支持向量机，朴素贝叶斯，随机森林，Bi-LSTM 和 BERT：

a) 在原有数据集上训练后，相比原测试集，反事实数据集上的测试结果要差许多。反之亦然。

b) 在结合了反事实增强过的训练集上训练，模型性能相比原来有着巨大的提升。

c) BERT 不但在通常情况下表现最好，而且在反事实干扰的数据集上表现也降低得最少

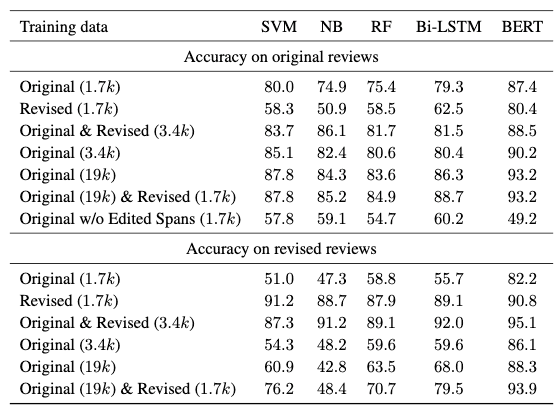
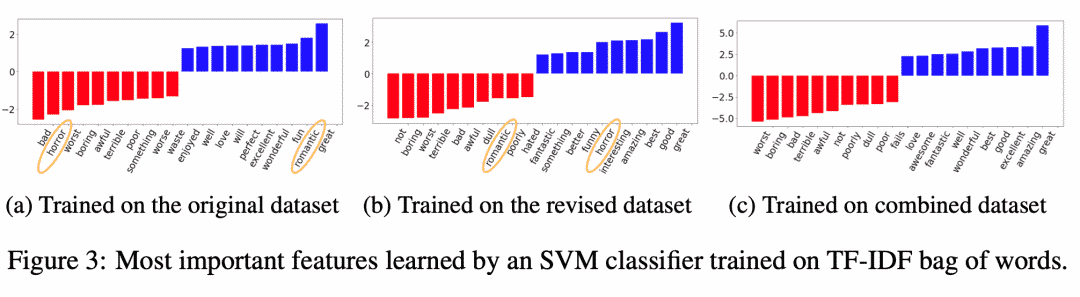
在案例分析中，研究者们也表明增强后模型排除了原来模型学习到的一些伪关键特征。

Counterfactuals Uncover the Modular Structure of Deep Generative Models

有监督的视觉模型很容易会被伪关系干扰从而学出带有偏见的结果。比如，一个典型的例子是有监督 CNN 模型在识别狼和狗的图片时，实际上使用的统计特征是狼一般在雪中而狗在草地上。也就是说，模型认为“背景（草或雪）”与“目标（狗和狼）”之间存在某种关系。而实际上，这两种特征是解耦合的。我们希望能找到某些能学会解耦合的特征表示的模型。

一个自然地验证模型解耦合能力的想法，是检验模型能否推理反事实情况（比如狗在雪中，狼崽草上）。这样的反事实推理能力也是人类智能的一个重要标志，即推理未发生事件的结果的能力，属于因果学习的一个重要分支。反事实理论在计量经济学和公共卫生领域得到了广泛的应用，然而对于机器学习，这套理论的应用方法仍然是一片空白。

将因果学习应用在表示学习上的一个重要改进的方向，就是来自 Max Planck Institut e的 Scho ̈lkopf 和 MILA 的 Bengio 目前倡议的 causal representation learning. 本文即是Scho ̈lkopf在 ICLR 2020 上的一篇尝试性的工作：通过验证模型推断反事实的能力，来验证生成式模型（BigGAN）可以学习到解耦合的模块化结构。

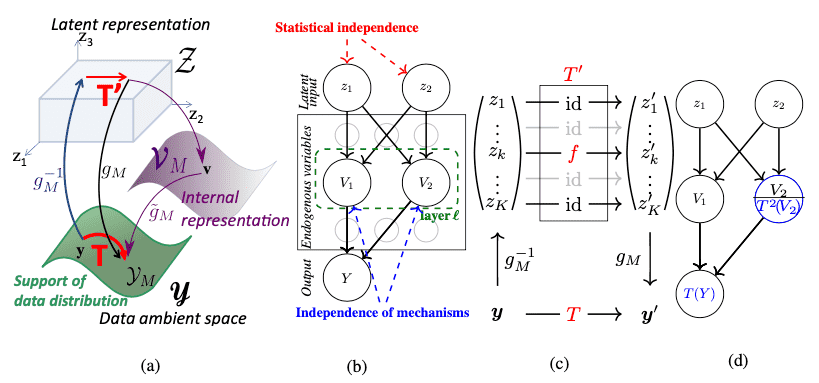
这篇工作基于一个重要假设：负责生成不同内容的因果机制，对最终生成结果的贡献是相互独立的。因此，如果我们能学到具有解耦合能力的表示模型，则各个模块在被干预(intervene)的结果应该是互不影响的。在此基础上，他们提出了因果生成模型（Causal Generative Model）的分析框架来解耦合生成式模型的模块化结构，如下图所示。

a)表述了生成映射和分离变换 T（表示对某个特征 z_2 的干预，不会对其他特征在任一表示空间的值产生影响）

b) CGM模型的因果图，V_1, V_2 表示不同的模块是独立的

c)稀疏变换在 latent space 上的机理

d)内在分离变换的表示