直播 | ICLR论文解读：如何利用变分自编码模型框架求解深度主题模型

分享背景

在如今大数据背景下，人们轻而易举的可以获得海量的文本数据，如何有效的分析这些文本数据，同时提取有效的特征用于后续的文本分类，文本检索以及推荐系统等应用中，成为一个重要的研究课题。虽然一些基于概率生成网络的主题模型被提出，比如 LDA ，深度 LDA 等，但是它们在测试阶段仍然需要耗费大量的时间去推理参数的后验，使得这些模型在实际应用的时效性上大打折扣。因此，本次公开课，张昊博士将结合他们团队 ICLR 2018 文章，WHAI: Weibull Hybrid Autoencoding Inference for Deep Topic Modeling，分享他在解决这个问题过程中的建模，算法实现以及实践经验。

分享题目

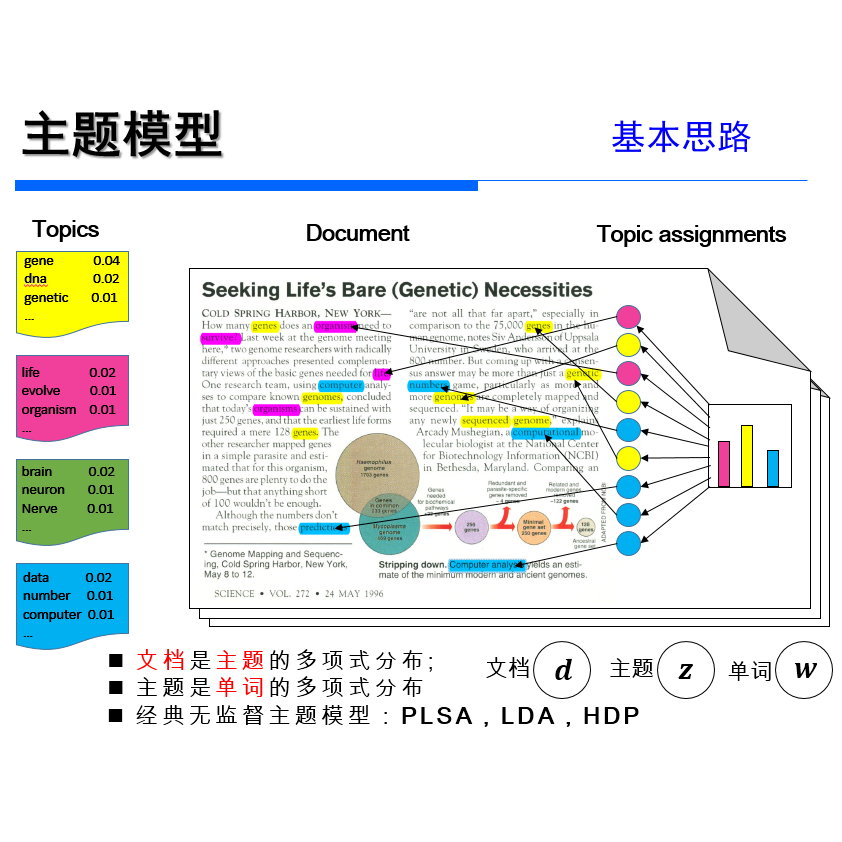
如何利用变分自编码模型框架求解深度主题模型

分享提纲

1. 大数据时代下的文本分析在很多系统中起到非常重要的作用。比如文本分类，文本检索以及推荐系统等。

2. 介绍基于概率生成模型的文本建模方法，并分析现有模型与算法的优缺点。

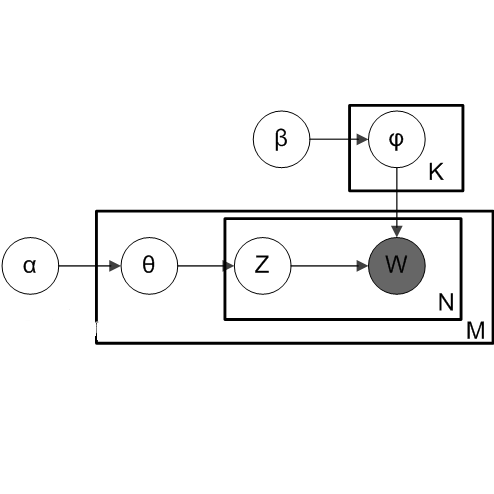
3. 深度 LDA（DLDA）模型是最近被提出的一种层次化主题模型，一些简单的推理算法，比如 Gibbs 采样，SG-MCMC 算法已经可以较好的去求解模型。

4. 结合我们团队在 ICLR2018 发表的文章，WHAI: Weibull Hybrid Autoencoding Inference for Deep Topic Modeling，从原理与应用背景两个层面，讨论如何利用变分自编码模型框架更加有效的求解深度主题模型。

WHAI: Weibull Hybrid Autoencoding Inference for Deep Topic Modeling

https://openreview.net/forum?id=S1cZsf-RW

分享嘉宾

张昊，西安电子科技大学在读博士，师从电子工程学院陈渤教授。本科毕业于西安电子科技大学电子与信息工程专业。主要研究方向为基于概率统计模型的图像识别，文本分析与主题模型，以及动态时序数据分析等一系列问题的理论研究与应用。

分享时间

北京时间 5 月 7 日（周一）晚上 8:00

参与方式

扫描海报二维码关注微信公众号，点击 AI 进阶——公开课报名

对了，我们招人了，了解一下？

BAT资深算法工程师独家研发课程

最贴近生活与工作的好玩实操项目

班级管理助学搭配专业的助教答疑

学以致用拿offer，学完即推荐就业

┏(＾0＾)┛欢迎分享，明天见！