深度学习对大数据、大算力的硬性要求迫使越来越多的企业将模型训练任务外包给专门的平台或公司,但这种做法真的安全吗?
来自 UC Berkeley、MIT 和 IAS 的一项研究表明,你外包出去的模型很有可能会被植入后门,而且这种后门很难被检测到。
如果你是一家银行,对方可能会通过这个后门操纵你给何人贷款。
![]()
机器学习(ML)算法正越来越多地被用于不同领域,做出对个人、组织、社会和整个地球都有重大影响的决策。
当前的 ML 算法需要大量的数据和计算能力。
因此,很多个人和组织会把学习任务外包给外部供应商,包括亚马逊 Sagemaker、微软 Azure 等 MLaaS 平台以及其他小公司。
这种外包可以服务于许多目的:
首先,这些平台拥有广泛的计算资源,即使是简单的学习任务也需要这些资源;
其次,他们可以提供复杂 ML 模型训练所需的算法专业知识。
如果只考虑最好的情况,外包服务可以使 ML 民主化,将收益扩大到更广泛的用户群体。
在这样一个世界里,用户将与服务提供商签订合同,后者承诺返回一个按照前者要求训练的高质量模型。学习的外包对用户有明显的好处,但同时也引起了严重的信任问题。有经验的用户可能对服务提供商持怀疑态度,并希望验证返回的预测模型是否能达到提供商声称的准确性和稳健性。
但是用户真的能有效验证这些属性吗?在一篇名为《Planting Undetectable Backdoors in Machine Learning Models》的新论文中,来自 UC Berkeley、MIT 和 IAS 的研究者展示了一股强大的力量:一个有敌对动机的服务提供者可以在学习模型交付后很长时间内保持这种力量,即使是对最精明的客户。
![]()
论文链接:https://arxiv.org/pdf/2204.06974.pdf
这个问题最好通过一个例子来说明。假设一家银行将贷款分类器的训练外包给了一个可能包含恶意的 ML 服务提供商 Snoogle。给定客户的姓名、年龄、收入、地址以及期望的贷款金额,然后让贷款分类器判断是否批准贷款。为了验证分类器能否达到服务商所声称的准确度(即泛化误差低),银行可以在一小组留出的验证数据上测试分类器。对于银行来说,这种检查相对容易进行。因此表面上看,恶意的 Snoogle 很难在返回的分类器准确性上撒谎。
然而,尽管这个分类器可以很好地泛化数据分布,但这种随机抽查将无法检测出分布中罕见的特定输入的不正确(或意外)行为。更糟糕的是,恶意的 Snoogle 可能使用某种「后门」机制显式地设计返回的分类器,这样一来,他们只要稍稍改动任意用户的配置文件(将原输入改为和后门匹配的输入),就能让分类器总是批准贷款。然后,Snoogle 可以非法出售一种「个人资料清洗(profile-cleaning)」服务,告诉客户如何更改他们的个人资料才最有可能得到银行放款。当然,银行会想测试分类器遇到这种对抗性操作时的稳健性。但是这种稳健性测试和准确性测试一样简单吗?
在这篇论文中,作者系统地探讨了不可检测的后门,即可以轻易改变分类器输出,但用户永远也检测不到的隐藏机制。他们给出了不可检测性(undetectability)的明确定义,并在标准的加密假设下,证明了在各种环境中植入不可检测的后门是可能的。这些通用结构在监督学习任务的外包中呈现出显著的风险。
这篇论文主要展示了对抗者将如何在监督学习模型中植入后门。假设有个人想植入后门,他获取了训练数据并训练了一个带后门密钥的后门分类器,使得:
给定后门密钥,恶意实体可以获取任何可能的输入 x 和任何可能的输出 y,并有效地产生非常接近 x 的新输入 x’,使得在输入 x’时,后门分类器输出 y。
后门是不可检测的,因为后门分类器要「看起来」像是客户指定且经过认真训练的。
作者给出了后门策略的多种结构,这些结构基于标准加密假设,能够在很大程度上确保不被检测到。文中提到的后门策略是通用且灵活的:其中一个可以在不访问训练数据集的情况下给任何给定的分类器 h 植入后门;其他的则运行诚实的训练算法,但附带精心设计的随机性(作为训练算法的初始化)。研究结果表明,给监督学习模型植入后门的能力是自然条件下所固有的。
定义
。作者首先提出了模型后门的定义以及几种不可检测性,包括:
不可检测的黑盒后门
。作者展示了恶意学习者如何使用数字签名方案 [GMR85] 将任何机器学习模型转换为后门模型。然后,他(或他有后门密钥的朋友)可以稍加改动任何输入 x ∈ R^d,将其转变成一个后门输入 x’,对于这个输入,模型的输出与输入为 x 时不同。对于没有秘钥的人来说,发现任意一个特殊的输入 x(后门模型和原始模型在遇到这个输入时会给出不同的结果)都是困难的,因为计算上并不可行。也就是说,后门模型其实和原始模型一样通用。
不可检测的白盒后门
。对于遵循随机特征学习范式的特定算法,作者展示了恶意学习者如何植入后门,即使给定对训练模型描述(如架构、权重、训练数据)的完全访问,该后门也是不可检测的。
具体来说,他们给出了两种结构:一是在 Rahimi 和 Recht 的随机傅里叶特征算法 [RR07] 中植入不可检测的后门;二是在一种类似的单层隐藏层 ReLU 网络结构中植入不可检测的后门。
恶意学习者的力量来自于篡改学习算法使用的随机性。研究者证明,即使在向客户揭示随机性和学习到的分类器之后,被植入这类后门的模型也将是白盒不可检测的——在加密假设下,没有有效的算法可以区分后门网络和使用相同算法、相同训练数据、「干净」随机 coin 构建的非后门网络。
在格问题的最坏情况困难度下(对于随机傅里叶特征的后门),或者在植入团问题的平均困难度下(对于 ReLU 后门),对手所使用的 coin 在计算上无法与随机区分。这意味着后门检测机制(如 [TLM18,HKSO21] 的谱方法)将无法检测作者提到的后门(除非它们能够在此过程中解决短格向量问题或植入团问题)。
该研究将此结果视为一个强大的概念验证,证明我们可以在模型中插入完全检测不到的白盒后门,即使对手被限制使用规定的训练算法和数据,并且只能控制随机性。这也引出了一些有趣的问题,比如我们是否有可能对其他流行的训练算法植入后门。
总之,在标准加密假设下,检测分类器中的后门是不可能的。这意味着,无论何时使用由不受信任方训练的分类器,你都必须承担与潜在植入后门相关的风险。
研究者注意到,机器学习和安全社区中有多项实验研究 [GLDG19、CLL+17、ABC+18、TLM18、HKSO21、HCK21] 已经探索了机器学习模型后门问题。这些研究主要以简单的方式探讨后门的不可检测性,但是缺乏正式定义和不可检测性的证据。通过将不可检测性的概念置于牢固的加密基础上,该研究证明了后门风险的必然性,并探究了一些抵消后门影响的方法。
该研究的发现对于对抗样本的稳健性研究也产生了影响。特别是,不可检测后门的结构给分类器对抗稳健性的证明带来很大的障碍。
具体来说,假设我们有一些理想的稳健训练算法,保证返回的分类器 h 是完全稳健的,即没有对抗样本。该训练算法存在不可检测的后门意味着存在分类器
![]() ,其中每个输入都有一个对抗样本,但没有有效的算法可以将
,其中每个输入都有一个对抗样本,但没有有效的算法可以将
![]() 与稳健分类器 h 区分开来。
这种推理不仅适用于现有的稳健学习算法,
也适用于未来可能开发的任何稳健学习算法。
如果无法检测到后门的存在,我们能否尝试抵消掉后门的影响?
该研究分析了一些可以在训练时、训练后和评估前以及评估时应用的潜在方法,阐明了它们的优缺点。
可验证的外包学习。在训练算法标准化的环境中,用于验证 ML 计算外包的形式化方法可用于在训练时缓解后门问题 。在这样的环境中,一个「诚实」的学习者可以让一个有效的验证器相信学习算法是正确执行的,而验证器很可能会拒绝任何作弊学习者的分类器。不可检测的后门的结构强度让这种方法存在缺点。白盒结构只需要对初始随机性进行后门处理,因此任何成功的可验证外包策略都将涉及以下 3 种情况的任何一种:
一方面,证明者在这些外包方案中的工作远不止运行诚实算法;但是,人们可能希望可验证外包技术成熟到无缝完成的程度。更严重的问题是,该方法只能处理纯计算外包场景,即服务提供商只是大量计算资源的提供者。对于那些提供 ML 专业知识的服务提供商,如何有效解决后门不可检测问题依然是一个难题,也是未来的一个探索方向。
梯度下降的考验。如果不验证训练过程,客户可能会采用后处理策略来减轻后门的影响。例如,即使客户想要外包学习(delegate learning),他们也可以在返回的分类器上运行几次梯度下降迭代。直观地讲,即使无法检测到后门,人们可能也希望梯度下降能破坏其功能。
此外,人们希望大幅减少迭代次数来消除后门。然而,该研究表明基于梯度的后处理效果可能是有限的。研究者将持久性(persistence)的概念引入梯度下降,即后门在基于梯度的更新下持续存在,并证明基于签名方案的后门是持久的。了解不可检测的白盒后门(特别是随机傅里叶特征和 ReLU 的后门)可以在梯度下降中存在多久是未来一个有趣的研究方向。
随机评估。最后,研究者提出了一种基于输入的随机平滑的时间评估抵消机制(evaluation-time neutralization mechanism)。具体来说,研究者分析了一种策略:在添加随机噪声后评估输入上的(可能是后门的)分类器。其中关键的是,噪声添加机制依赖于对后门扰动幅度的了解,即后门输入与原始输入的差异有多大,并在稍大半径的输入上随机进行 convolving。
如果恶意学习者对噪声的大小或类型有所了解,他就可以提前准备可以逃避防御的后门扰动(例如通过改变大小或稀疏度)。在极端情况下,攻击者可能会隐藏一个需要大量噪声才能进行抵消的后门,这可能会使返回的分类器无用,即使在「干净」的输入上也是如此。因此,这种抵消机制必须谨慎使用,不能起到绝对的防御作用。
总之,该研究表明存在完全无法检测到的后门,研究者认为机器学习和安全研究社区进一步研究减轻其影响的原则方法至关重要。
与稳健分类器 h 区分开来。
这种推理不仅适用于现有的稳健学习算法,
也适用于未来可能开发的任何稳健学习算法。
如果无法检测到后门的存在,我们能否尝试抵消掉后门的影响?
该研究分析了一些可以在训练时、训练后和评估前以及评估时应用的潜在方法,阐明了它们的优缺点。
可验证的外包学习。在训练算法标准化的环境中,用于验证 ML 计算外包的形式化方法可用于在训练时缓解后门问题 。在这样的环境中,一个「诚实」的学习者可以让一个有效的验证器相信学习算法是正确执行的,而验证器很可能会拒绝任何作弊学习者的分类器。不可检测的后门的结构强度让这种方法存在缺点。白盒结构只需要对初始随机性进行后门处理,因此任何成功的可验证外包策略都将涉及以下 3 种情况的任何一种:
一方面,证明者在这些外包方案中的工作远不止运行诚实算法;但是,人们可能希望可验证外包技术成熟到无缝完成的程度。更严重的问题是,该方法只能处理纯计算外包场景,即服务提供商只是大量计算资源的提供者。对于那些提供 ML 专业知识的服务提供商,如何有效解决后门不可检测问题依然是一个难题,也是未来的一个探索方向。
梯度下降的考验。如果不验证训练过程,客户可能会采用后处理策略来减轻后门的影响。例如,即使客户想要外包学习(delegate learning),他们也可以在返回的分类器上运行几次梯度下降迭代。直观地讲,即使无法检测到后门,人们可能也希望梯度下降能破坏其功能。
此外,人们希望大幅减少迭代次数来消除后门。然而,该研究表明基于梯度的后处理效果可能是有限的。研究者将持久性(persistence)的概念引入梯度下降,即后门在基于梯度的更新下持续存在,并证明基于签名方案的后门是持久的。了解不可检测的白盒后门(特别是随机傅里叶特征和 ReLU 的后门)可以在梯度下降中存在多久是未来一个有趣的研究方向。
随机评估。最后,研究者提出了一种基于输入的随机平滑的时间评估抵消机制(evaluation-time neutralization mechanism)。具体来说,研究者分析了一种策略:在添加随机噪声后评估输入上的(可能是后门的)分类器。其中关键的是,噪声添加机制依赖于对后门扰动幅度的了解,即后门输入与原始输入的差异有多大,并在稍大半径的输入上随机进行 convolving。
如果恶意学习者对噪声的大小或类型有所了解,他就可以提前准备可以逃避防御的后门扰动(例如通过改变大小或稀疏度)。在极端情况下,攻击者可能会隐藏一个需要大量噪声才能进行抵消的后门,这可能会使返回的分类器无用,即使在「干净」的输入上也是如此。因此,这种抵消机制必须谨慎使用,不能起到绝对的防御作用。
总之,该研究表明存在完全无法检测到的后门,研究者认为机器学习和安全研究社区进一步研究减轻其影响的原则方法至关重要。
![]()
![]()
![]()
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
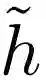 ,其中每个输入都有一个对抗样本,但没有有效的算法可以将
,其中每个输入都有一个对抗样本,但没有有效的算法可以将
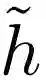 与稳健分类器 h 区分开来。
这种推理不仅适用于现有的稳健学习算法,
也适用于未来可能开发的任何稳健学习算法。
与稳健分类器 h 区分开来。
这种推理不仅适用于现有的稳健学习算法,
也适用于未来可能开发的任何稳健学习算法。