“蝴蝶效应”也能预测了?看机器学习如何解释混沌系统
大数据文摘作品
编译:李雷、笪洁琼、夏雅薇
一只南美洲的蝴蝶,偶尔扇动几下翅膀,两周后可以引起美国德克萨斯州的一场飓风……
极小的扰动,将会引起结果的巨大差异。不可重复、不可预测,这就是混沌现象。
不可预测?那么,有了机器学习之后呢?
半个世纪前,混沌理论的先驱们发现由于存在“蝴蝶效应”,长期预测是不可能的。对于复杂系统(如天气,经济等等),即使是最小的扰动也能触发一连串事件,导致极为不同的后果。
我们生活在不确定的阴影之下,无法确定这些系统的状态以预测它们将如何发展。
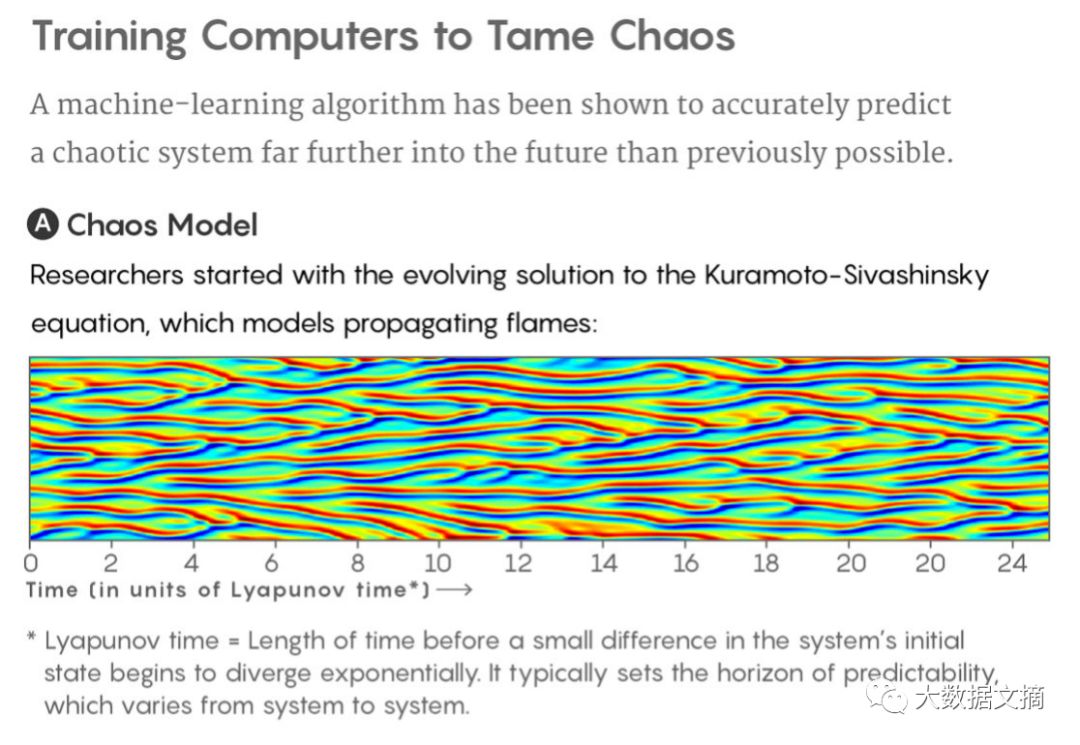
最近,美国马里兰大学的研究表明,人工智能算法可以预测混沌系统的发展趋势。比如,预测模型火焰锋面的混沌演进过程:
大数据文摘后台对话框内回复“混沌”即可下载这篇论文~
德国不来梅雅各布大学计算科学教授Herbert Jaeger表示:“这种方法真的很了不起,能够预测一个系统的混沌演进将会进行到什么地步。”
这个发现来自老牌混沌理论家Edward Ott和马里兰大学的四名合作者。他们采用了一种叫做储备池计算(reservoir computing)的机器学习算法来“学习”原型混沌系统动力学,又叫做Kuramoto-Sivashinsky方程式(非线性偏微分方程)。这个方程式的演进解决方案就像一个火焰锋面,在可燃介质中闪烁前行。
Ott的研究生、论文的一作Jaideep Pathak说,这个方程式还描述了等离子体中的漂移波和其他现象,可以作为“研究湍流和时空混沌的测试平台”。
论文作者们
机器学习的优势何在?
在用Kuramoto-Sivashinsky方程的演进数据进行训练后,计算机算法可以近似地预测火焰系统在未来八个李亚普诺夫时间(Lyapunov times)长度的演进。李亚普诺夫时间表示混沌系统的两个几乎完全相同的状态需要多长时间才能呈指数发散。
机器学习的方法能预测到的未来大大延长,比此前的预测方法能预测到的长了八倍,预测效果几乎和真实情况完全匹配。
而且,这个算法对Kuramoto-Sivashinsky方程式本身一无所知;它只能看到方程式演进的数据。
这使机器学习方法变得更强大。因为,在许多情况下,由于不能确定描述混沌系统的方程式,动力学家无法对它们进行建模和预测。
现在,不再需要公式,只要数据就可以了。
专家认为,这篇论文表明未来我们或许能够通过机器学习算法来预测天气,而不是通过复杂的大气模型。
除了天气预报外,机器学习技术还可以帮助监测心律失常,从而预测即将发生的心脏病,并监测大脑中神经突起的神经元放电模式。更进一步,它或许能帮助预测那些会危及船只甚至可能导致地震的超级巨浪。
此外,我们也许能够提前预警太阳风暴,比如1859年横越太阳表面35,000英里的太阳风暴。那次磁力暴风导致了出现在全球各地的北极光,同时产生高压使通讯线路在没有电源的情况下仍有电流通过,从而摧毁了部分电报系统。
如果这样的太阳风暴现在袭击地球,将严重损害地球的电子基础设施。但是如果你能预测到风暴即将到来,就可以暂时关掉电子设备电源,等风暴过后再打开。
算法预测混沌系统的原理
混沌模型:研究人员从模拟火焰锋面传播的Kuramoto-Sivashinsky方程式开始。
*李亚普诺夫时间=系统初始状态的微小差异开始呈指数发散之前的时间长度。它通常设定因系统而异的可预测性的范围。
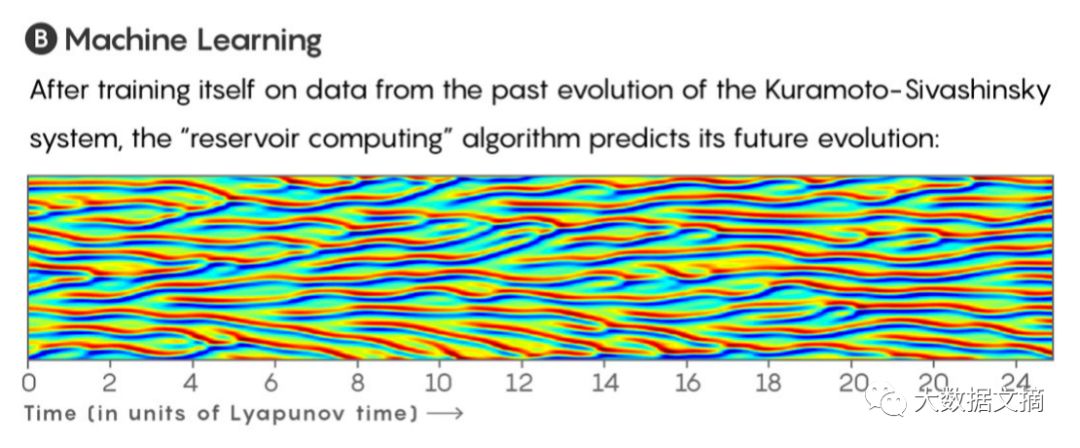
用Kuramoto-Sivashinsky系统过去的演进数据进行训练后,“储水池计算”算法预测其未来演进。
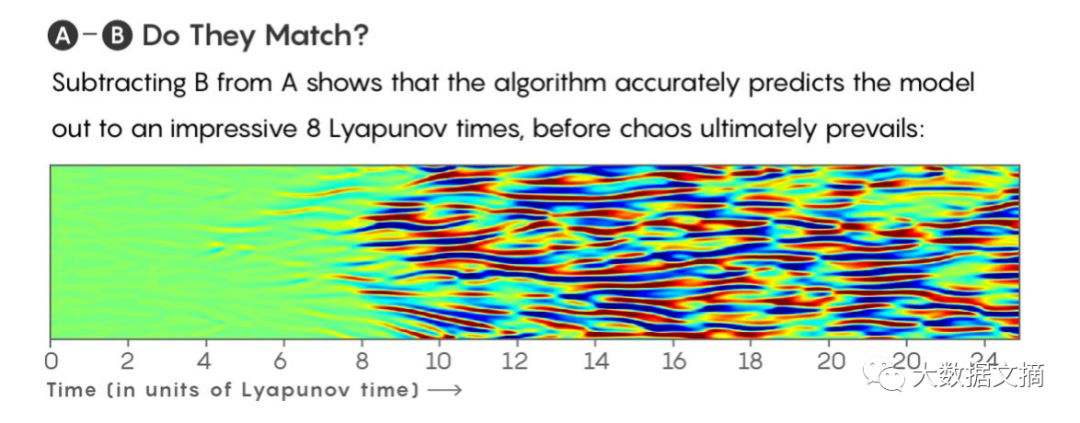
令人赞叹的是,在混沌最终占优势之前,该算法可以精确地预测出模型的8个李亚普诺夫时长时间内的演进。
这一成果是通过综合现有的工具和算法得来。
当强大的“深度学习”算法开始征服像图像和语音识别等人工智能任务时,Ott和他的同事们开始研读机器学习并思考如何将其应用于混沌理论。
他们发现,2004年,Herbert Jaeger和Harald Haas利用一个随机连接人造神经元的网络在储水池计算中形成“储水池”,从而学习有三个混沌协变变量的动力学方程。在使用三组数字进行训练之后,这个网络可以预测未来很长一段时间内三个变量的值。不过,当有多个相互作用的变量时,计算量会变得很庞大。
但是,需要一个更有效的方案来将储水池计算与大型混沌系统联系起来,因为这些混沌系统具有大量相互作用的变量。例如,需要跟踪沿着火焰前进方向的每一点在三个空间方向上的速度分量。
他们花了几年时间才找到了明确的解决方案。Pathak说:“我们利用的是空间扩展混沌系统中相互作用的局部性。”
局部性意味着变量在一个地方受到附近变量的影响,但不受远处变量的影响。利用它可以从本质上将问题分块。也就是说,可以将问题并行化,用一个神经元储水池来学习系统的一小块,另一个储水池学习另一块,如此类推,并且使相邻域轻微重叠以表示它们之间的相互作用。
只要将计算机资源按比例分配给每个任务,并行化处理,就可以使用储水池计算的方法来处理几乎任意大小的混沌系统。
具体解释:三步走
储水池计算分三步。假设你想用它来预测火灾蔓延的情形,那么首先,选取火焰锋面的五个不同点测量火焰的高度,然后随着火焰跳动前行继续测量锋面上这些点的火焰高度。
将这些数据流输入到储水池中随机选择的人造神经元。输入的数据触发神经元释放信号,继而触发相邻的神经元并在整个网络中级联传输信号。
第二步是使神经网络从输入数据中学习不断演进的火焰锋面的动力学方程。要做到这一点,在输入数据时,还需要监测储水池中随机选择的几个神经元的信号强度。以五种不同方式对这些信号进行加权和组合可产生五个数字输出。
这样做的目的是调整用于计算输出的各种信号的权重,直到这些输出始终与下一组输入,也就是在比火焰锋面略晚的位置测得的新的五个高度,相匹配。所要的就是,把输出作为下一点的输入。
为了得到正确的权重,这个算法简单地将每组输出,或者说五点中的每一点的预测火焰高度,与下一组输入或实际火焰高度进行比较,每次增加或减少各种信号的权重,只要可以使它们的组合给出五个输出的正确值。
从一个时间步长到下一个,随着权重的调整,逐步改善预测,直到算法能够稳定预测一个时间步长后的火焰状态。
第三步,就可以真正去做预测了。了解了系统动力学方程的“储水池”可以揭示系统如何演进。神经网络本质上会自适应。输出反馈为新输入,其输出又再反馈为输入,以此循环,从而预测火焰锋面五个位置的高度将如何演进。其他并行的“储水池”预测其他地方的火焰高度的演进。
传统上,预测混沌系统的常用方法是某一时刻尽可能准确地测量其条件,使用这些数据校准物理模型,然后向前演进模型。如果要预测未来八倍时长的演进,需要对一个典型系统的初始条件进行100,000,000次以上的测量。
这就是为什么利用机器学习技术几乎能够知道真相了。
神经网络和混沌理论
最近,麻省理工学院和苏黎世联邦理工学院的研究人员取得了与马里兰团队相似的结果,使用“长短期记忆”神经网络,该网络具有周期性循环的特征,使其能够长时间存储临时信息。
Ott和他的同事们已经快可以将他们的预测技术用于实际应用。在《混沌》杂志即将发表的新研究中,他们展示了如何通过混合数据驱动的机器学习方法和传统的基于模型的预测,改进对像Kuramoto-Sivashinsky方程式这样的混沌系统的预测。
大数据文摘后台对话框内回复“混沌”下载以上两篇论文~
Ott认为这是改进天气预报和其他类似工作的更好的途径,因为我们并不总能找到完整的高分辨率数据或完美的物理模型。
“我们应该做的就是利用我们已有的经验。如果我们缺乏某些知识,就应该使用机器学习来填补所这些空白。”
储水池式预测本质上可以校准模型;在Kuramoto-Sivashinsky方程式的情况下,精确的预测可以延伸到12个李亚普诺夫时长。
李亚普诺夫时间的长度因不同系统而异,从毫秒到数百万年不等(对于天气预报情况来说是几天)。这个时间越短,系统就越敏感就会越容易产生蝴蝶效应,状态的发散会更快。
目前还不清楚究竟为什么储水池算法如此擅长学习混沌系统的动力学模型,只是知道计算机可以根据响应数据进行自调节,直到计算公式与混沌系统的动态完全一致。
研究人员现在正打算使用混沌理论来更好地理解神经网络的内部机制。
相关报道:
https://www.quantamagazine.org/machine-learnings-amazing-ability-to-predict-chaos-20180418/?from=singlemessage&isappinstalled=0
https://arxiv.org/abs/1710.07313
https://arxiv.org/pdf/1803.03365
【今日机器学习概念】
志愿者介绍
回复“志愿者”加入我们