它打败了欧几里得空间，踹飞了数学怪物，成为全世界的焦点

Long long ago，超模君为大家介绍Koch曲线的时候提到了分形，结果小天很好奇这个所谓的分形究竟是什么。

为了不让小天老是纠缠这个问题，今天超模君就来介绍一下分形吧。

数千年以来，几何学的研究主要集中在欧几里得几何上。正因如此，欧式几何一直是人类认识自然物体形状的有力工具，还是各种学科理论的基础。甚至伽利略曾断言：“大自然的语言是数学，它的标志是三角形、圆和其他几何图形”。

 但，真的是这样吗？

事实并非如此，自然界中存在着各种不规则不光滑不连续的几何形体，譬如湍流的高漩涡、河流的支流、蜿蜒的海岸线，而这些形体是无法用欧式几何描述的。

既然“万能”的欧式几何不管用了，那么有没有处理这些不规则形体的好方法呢？

显然是没有的。

因此在1个多世纪前，所谓的数学怪物出现了，而康托尔、魏尔斯特拉斯等数学家则成为了制造者。

1883年，康托尔引入了如今广为人知的康托尔集，也称为三分集。虽然康托尔集很容易构造，还是个测度为0的集，也就是它的函数图像面积为0，但它具备很多最典型的分形特征，因此康托尔始终无法解决。

目前分形几何的特征有：在任意小的尺度上都能有精细的结构； 太不规则； （至少是大略或任意地）自相似，豪斯多夫维数会大於拓扑维数（但在空间填充曲线如希尔伯特曲线中为例外）； 有著简单的递归定义。

Cantor集

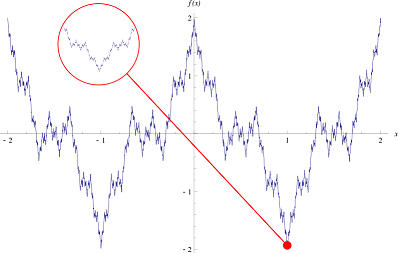
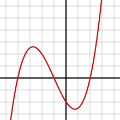
1895年，在大部分数学家认为除了少数特殊的点以外，连续的函数曲线在每一点上总会有斜率的情况下，魏尔斯特拉斯提出了第一个分形函数“魏尔斯特拉斯函数”，并凭借函数曲线特点“处处连续，处处不可微”证明了所谓的“病态”函数的存在性。

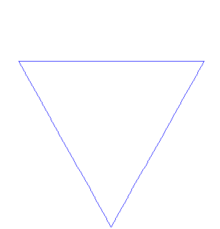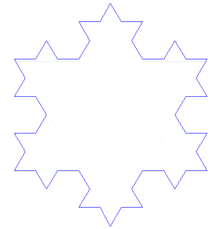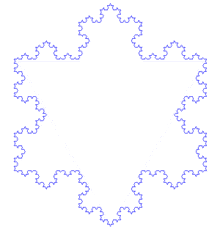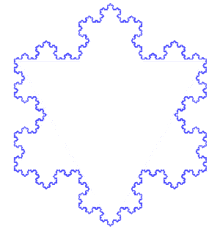
1906年，科赫在论文《关于一条连续而无切线，可由初等几何构作的曲线》中提到了一种像雪花的几何曲线，而这个雪花曲线就是de Rham曲线的特例科赫曲线。

Koch曲线

1914年，波兰数学家谢尔宾斯基利用等边三角形进行分形构造，提出了谢尔宾斯基三角形；两年后，利用正方形进行分形构造提出了谢尔宾斯基地毯。

谢尔宾斯基三角形和谢尔宾斯基地毯（3D）

之后的59年间，陆续有人研究出相关的分形情况，但始终都没有人能够消灭这些数学怪物，直到“分形学之父”Benoit Mandelbrot（本华·曼德博，又译为芒德布罗）误打误撞发现了一只臭虫，诞生了真正属于自然界的几何学——分形几何，才彻底解决。

Benoit Mandelbrot

1961年，在IBM担任研究员的Mandelbrot收到了解决阻止信号传输的白噪声的任务。虽然任务相当简单，但是Mandelbrot被要求提供新的解决方案，因此他只好借助自身擅长可视化思考问题的优势来探索解决方法。

于是在从形状上观察白噪声的时候，Mandelbrot发现白噪声转换而成的扰动图形揭示了一种奇怪的特征：无论图形的比例是多大，无论数据代表的时长是多少，扰动模式基本一致。

这很奇怪，谁能告诉我为什么

这个奇怪的特征让Mandelbrot甚是苦恼，不过他有个好叔叔。因为他的叔叔佐列姆·芒德勃罗伊（Szolem Mandelbrojt）曾经建议他研究研究皮埃尔·法图（Pierre Fatou）和加斯顿·朱利亚（Gaston Julia）建立的迭代理论和公式z = z2 + c。

公式采用变量z和参数c，映射了复平面上的数值。其中x轴测量复数的实数部分，而 y 轴测量复数的虚数部分。

而正是因为这个建议，在借助IBM家的高性能计算机的情况下，Mandelbrot通过迭代对数字进行了成千上万次的运算和处理，最终成功绘制输出值的图形—一个形似臭虫的图形。

迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。

没错，这就是那只臭虫

图形的成功绘制并没有让Mandelbrot过于兴奋，因为他在细心观察后发现这只臭虫的小触角跟大触角的形状是一样的，但是结构并不完全一样，每一个小触角比前一个触角更为复杂。也就是说全部触角的形状都很相似，但是细节存在不同之处。

Mandelbrot对此甚感兴趣，进行深入研究后得出细节的特异性仅限于计算等式所用的机器的能力，而形状的相似可以永远持续下去—无限地揭示越来越多的细节。随后，Mandelbrot就觉察出自己无意中有了能够震惊数学界的发现—一种新的几何学。

对于这类重复的或者自身相似的数学图形，Mandelbrot在1975年提出了“分形”（Fractal），紧接着在1967年，他发表了题为《英国的海岸线有多长》的划时代论文，萌生出分形思想。

此后，Mandelbrot越发勤奋地进行研究，陆续出版了《分形学：形态，概率和维度》（法文）、《分形：形状，机遇和维数》（英译本）和《大自然的分形几何》（第一版），但是这三本书并没引起人们对分形的注意。

直到1982年出版的《大自然的分形几何》（第二版）才让分形几何彻底走进公众的视野，而通过描述树，Mandelbrot指出了分形几何适用于自然物质。

就这样，分形几何学诞生了（而分形几何还没有一个标准统一的定义），与此同时，此书成为了分形学界的“圣经”。

实际上，Mandelbrot创造的分形几何学具有极为重要的影响，它很快就进入了主流数学研究范畴，帮助数学家们彻底解决了困扰着大家N年的数学怪物，还对非负实数维数进行研究，形成分形理论，并应用于多个领域。

“ Mandelbrot集”（曼德博集）

不要以为分形学很高级，它的应用我们接触不到。不是这样的，分形几何其实无处不在，离我们最近的要数身体中的生理过程了。

举个栗子！

在过去很长时间里，科学家们一直认为人类的心脏是以规则的线性形式跳动，然而真正健康的心脏的心率是以特殊的不规则形式跳动的。同样，体内的血液也是以不规则方式在人体内分布。

借助分形几何，医生无需借助更清晰的医学图像或者更强大的机器就可看到人体器官癌变前的结构，并能通过分形学生成的数学模型更早的检测出癌变细胞，而非显微镜。

生物和医疗只是分形几何的其中两个最新应用领域，而更加为人所知的应该就是分形艺术了。

最开始将艺术和数学联系在一起还是Mandelbrot，他向世界展示了这两个领域并非互相排斥的，之后分形艺术便一发不可收拾。

分形艺术不同于普通的“电脑绘画”，它主要利用分形几何学原理，借助计算机强大的运算能力，将数学公式反复迭代运算，再结合创作者的审美及美术功底，就将创作出一幅幅精美的艺术画作。

数学之美是非常令人兴奋、鼓舞人心的，并且我们一直在研究，一直在研究，看不到终点。

————

编辑 ∑ Gemini

来源：超级数学建模

微信公众号“算法数学之美”，由算法与数学之美团队打造的另一个公众号，欢迎大家扫码关注！

更多精彩：

☞如何向5岁小孩解释什么是支持向量机（SVM）？

☞自然底数e的意义是什么？

☞费马大定理，集惊险与武侠于一体

☞简单的解释，让你秒懂“最优化” 问题

☞一分钟看懂一维空间到十维空间

☞ 本科、硕士和博士到底有什么区别？

☞小波变换通俗解释

☞微积分必背公式

☞影响计算机算法世界的十位大师

☞数据挖掘之七种常用的方法

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域，经采用我们将奉上稿酬。

投稿邮箱：math_alg@163.com