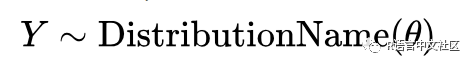R 语言之数据分析高级方法「GLM 广义线性模型」
作者:姚某某
博客:https://zhuanlan.zhihu.com/mydata
往期回顾:
本节主要总结「数据分析」的「GLM 广义线性模型」思想。
「知其然,而不知其所以然」是一种很肉痛的感觉。
《 R 语言实战》一书,从第 13 章开始,进入了数据分析高级方法的介绍,这些方法对于初学者而言,都显的有些高深莫测。虽然能够正确的将书中代码实现并得到正确的结果,但是总有一种抱着人家孩子却体会不到人家造人快感的难受,所有我每实践一种新的方法都天真的想去抓住这些方法的本质,甚至挖掘其来龙去脉,事实证明果然是真的天真,每一种方法的背后都有着一整套的理论体系,要想彻底弄清所有细节,非一日之功。所以,我选择了退一步,只力求理解其理论思想,不纠结其公式推导,算法的深入研究留给将来的实践过程。
本节,我就讲一讲对「GLM 广义线性模型」的理解。
1. 广义线性模型理解
1.1. 个人对广义线性模型的理解
广义线性模型,其实没想象中那么吓人,但是大多数文章中的解释都太过公式化,初学者很难从这些抽象的数学推导中去总结宏观的思维过程,直到看到了这个问题「广义线性模型和联系函数」中@Jack Diamond的回答,我才有一种恍然大悟的感觉。
相较与标准线性模型,广义线性模型有两个推广:
响应变量 Y 在标准线性模型中服从于参数为的正态分布(μY,δ2),推广到广义线性模型中,响应变量 Y 服从于指数分布族中的一种分布即可,相关参数根据具体分布而定。(这个指数分布族的坑就很深,手头上没有相关项目我还没有打算花时间去填,只要记住几个常用的指数分布目前也就够用了,比如二项分布、泊松分布等)
线性含义的推广。在标准线性模型中,线性指的是,响应变量 Y 所服从的正态分布的参数 μY 是线性的,即 μY =a + bx 当然这个线性可以从 x 这个角度做其他推广,多元、非线性之类)。而在广义线性模型中,线性推广至,响应变量 Y 所服从的一个分布(指数分布族)的参数θ它的函数 f(θ)是线性的,即(同样可以从 f(θ)= a + bx 这个角度做其他推广,这里的 f(θ) 我们称为联结函数)。
1.2. 举例
1.2.1. 标准线性回归
用广义线性模型表示 Y~(μY,δ2) ,其中 μY =a + bx 。
1.3. 总结
Jack Diamond 的总结已经很到位:
一般地说,GLM的建模过程是这样的:首先弄清楚 y 服从什么分布,写出
公众号后台回复关键字即可学习
回复 R R语言快速入门及数据挖掘
回复 Kaggle案例 Kaggle十大案例精讲(连载中)
回复 文本挖掘 手把手教你做文本挖掘
回复 可视化 R语言可视化在商务场景中的应用
回复 大数据 大数据系列免费视频教程
回复 量化投资 张丹教你如何用R语言量化投资
回复 用户画像 京东大数据,揭秘用户画像
回复 数据挖掘 常用数据挖掘算法原理解释与应用
回复 机器学习 人工智能系列之机器学习与实践
回复 爬虫 R语言爬虫实战案例分享