如何建立预测大气污染日的概率预测模型

2018 年 9 月 23 日 AI研习社

本文为 AI 研习社编译的技术博客，原标题：

How to Develop a Probabilistic Forecasting Model to Predict Air Pollution Days

翻译 | 就2 校对 | 就2 整理 | 志豪

原文链接：

https://machinelearningmastery.com/how-to-develop-a-probabilistic-forecasting-model-to-predict-air-pollution-days/

如何建立一个概率预测模型来预测空气污染的天数

空气污染的特征是地面臭氧的浓度。

从风速和温度等气象测量数据，可以预测地面臭氧是否会在明天达到足以发出公众空气污染警告的高度。（目前主要污染检测指标为，VOCs（有机挥发化合物）、PM2.5（PM10）、臭氧O₃，本文只讨论臭氧污染）。

这是用于时间序列分类数据集的标准机器学习数据集的基础，简称为“臭氧预测问题”。这个数据集描述了休斯顿地区7年来的气象观测，以及臭氧水平是否高于临界空气污染水平。

在本教程中，您将了解如何探索这些数据，并开发一个概率预测模型来预测德克萨斯州休斯顿的空气污染。

阅读完本教程后，您将知道:

如何加载和准备臭氧日标准机器学习预测建模问题。
如何开发一个基础的预测模型，并利用Brier技能得分（编者按：Brier得分=（实际结果-预测概率）的均方误差）对预测进行评估。
如何使用决策树的集合并通过超参数调优技巧进一步提高基础预测模型以此得到成功模型。

让我们开始吧。

照片版权归属 paramita

教程概述

本教程分为五个部分：

臭氧预测问题
加载和检查数据
基础的预测模型
集成树预测模型
梯度提升优化模型

臭氧预测问题

空气污染之一可被描述为地面臭氧的高含量，通常被描述为“坏臭氧”，以区别于高层大气中的臭氧。
臭氧预测问题是一个时间序列分类预测问题，涉及到预测第二天是否会出现高空气污染日(臭氧日)。
气象组织可以利用臭氧日的预测来警告公众，以便采取预防措施。
该数据集最初是由张坤（ Kun Zhang）等人在2006年发表的论文《预测偏差随机臭氧天：分析和解决方案”》中研究的，然后在他们的后续论文《预测偏差随机臭氧日:分析、更进一步的解决方案》中再次研究。
这是一个具有挑战性的问题，因为构成高臭氧水平的物理机制已经(或没有)被完全理解，这意味着预测不能像其他气象预测那样基于物理模拟，比如温度和降雨。
该数据集被用作开发预测模型的基础，这些模型使用了一系列变量，这些变量可能与臭氧水平的预测有关，也可能与臭氧水平的预测无关，此外还有一些已知的与实际化学过程相关的变量。

然而，环境科学家普遍认为，目前还没有开发的大量其他特征很可能有助于建立高度精确的臭氧预测模型。然而，这些特征究竟是什么，以及它们在形成臭氧过程中是如何相互作用的，人们知之甚少。今天的环境科学还不知道如何使用它们。这为数据挖掘提供了绝佳的机会（编者：这就是炼丹修仙的良机）。

-----预测偏差随机臭氧天：分析和解决方案” 2016

在接下来的日子预测高水平的地面臭氧是一个具有挑战性的问题：众所周知这具有随机性质，也意味着预期会出现预测错误。因此，有必要对预测问题进行概率建模，并预测臭氧日或前一天未观测到臭氧的可能性。

该数据集包含了7年的每日气象观测数据(1998-2004年或2536天)，在美国德克萨斯州休斯顿、加尔维斯顿和布拉多利亚地区是否有臭氧日。

每天总共观察72个变量，其中许多被认为与预测问题有关，其中的10个根据物理原理被证实与预测问题有关。

[……]在这72个特征中，只有10个特征被环境科学家证实是有用和相关的，迄今为止，关于其他60个特征的相关性，既没有实证也没有理论资料。然而，空气质量控制的科学家们长期以来一直在推测，这些特征中的一些可能有用，但只是无法发展理论或使用模拟来证明它们的相关性。

----预测偏差随机臭氧天数:分析和解决方案，2006。

这里有24个变量跟踪依赖于每小时的风速，另外24个变量跟踪依赖一天中每小时的温度。数据集的两个版本可用于度量的不同平均周期，分别是1小时和8小时。

似乎缺少的和可能有用的是每天观察到的臭氧，而不是直接二分为：臭氧日/非臭氧日。且参数模型中使用的其他度量方法也不可用。
有趣的是，一个参数臭氧预测模型被用作基线，基于1999年环保署指南“臭氧预测项目指南”的描述。本文件还描述了验证臭氧预测系统的标准方法。
综上所述，这是一个具有挑战性的预测问题，因为:

有许多特征，其重要性暂时大家都不知道。
输入特征及其相互关系可能随时间而变化。
许多需要处理的特征都缺少观察结果。
非臭氧日(非事件)远远多于臭氧日(事件)，这使得样例高度不平衡。

加载和检查数据

该数据集可从UCI机器学习库获得，也可以在文章最后的github上下载。

臭氧水平检测数据集

我们将只查看本教程中的8小时数据。下载“eighthr.data”并将其放在当前工作目录中。

检查数据文件，我们可以看到不同尺度的观察结果。

1/1/1998,0.8,1.8,2.4,2.1,2,2.1,1.5,1.7,1.9,2.3,3.7,5.5,5.1,5.4,5.4,4.7,4.3,3.5,3.5,2.9,3.2,3.2,2.8,2.6,5.5,3.1,5.2,6.1,6.1,6.1,6.1,5.6,5.2,5.4,7.2,10.6,14.5,17.2,18.3,18.9,19.1,18.9,18.3,17.3,16.8,16.1,15.4,14.9,14.8,15,19.1,12.5,6.7,0.11,3.83,0.14,1612,-2.3,0.3,7.18,0.12,3178.5,-15.5,0.15,10.67,-1.56,5795,-12.1,17.9,10330,-55,0,0.
1/2/1998,2.8,3.2,3.3,2.7,3.3,3.2,2.9,2.8,3.1,3.4,4.2,4.5,4.5,4.3,5.5,5.1,3.8,3,2.6,3,2.2,2.3,2.5,2.8,5.5,3.4,15.1,15.3,15.6,15.6,15.9,16.2,16.2,16.2,16.6,17.8,19.4,20.6,21.2,21.8,22.4,22.1,20.8,19.1,18.1,17.2,16.5,16.1,16,16.2,22.4,17.8,9,0.25,-0.41,9.53,1594.5,-2.2,0.96,8.24,7.3,3172,-14.5,0.48,8.39,3.84,5805,14.05,29,10275,-55,0,0.
1/3/1998,2.9,2.8,2.6,2.1,2.2,2.5,2.5,2.7,2.2,2.5,3.1,4,4.4,4.6,5.6,5.4,5.2,4.4,3.5,2.7,2.9,3.9,4.1,4.6,5.6,3.5,16.6,16.7,16.7,16.8,16.8,16.8,16.9,16.9,17.1,17.6,19.1,21.3,21.8,22,22.1,22.2,21.3,19.8,18.6,18,18,18.2,18.3,18.4,22.2,18.7,9,0.56,0.89,10.17,1568.5,0.9,0.54,3.8,4.42,3160,-15.9,0.6,6.94,9.8,5790,17.9,41.3,10235,-40,0,0.
...

浏览文件，例如2003年初，我们可以看到缺少的观察值标有“？”值。

...
12/29/2002,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,11.7,0.09,5.59,3.79,1578,5.7,0.04,1.8,4.8,3181.5,-13,0.02,0.38,2.78,5835,-31.1,18.9,10250,-25,0.03,0.
12/30/2002,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,10.3,0.43,3.88,9.21,1525.5,1.8,0.87,9.17,9.96,3123,-11.3,0.03,11.23,10.79,5780,17,30.2,10175,-75,1.68,0.
12/31/2002,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,8.5,0.96,6.05,11.18,1433,-0.85,0.91,7.02,6.63,3014,-16.2,0.05,15.77,24.38,5625,31.15,48.75,10075,-100,0.05,0.
1/1/2003,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,?,7.2,5.7,4.5,4,3.6,3.3,3.1,3.2,6.7,11.1,13.8,15.8,17.2,18.6,20,21.1,21.5,20.4,19.1,17.8,17.4,16.9,16.6,14.9,21.5,12.6,6.4,0.6,12.91,-10.17,1421.5,1.95,0.55,11.97,-7.78,3006.5,-14.1,0.44,20.42,-13.31,5640,2.9,30.5,10095,35,0,0.
...

首先，我们可以使用read_csv() 函数以 Pandas DataFrame 的形式加载数据。没有数据标头，我们可以解析第一列中的日期并将它们作为索引;下面列出了完整的示例。

# load and summarize
from pandas import read_csv
from matplotlib import pyplot
# load dataset
data = read_csv('eighthr.data', header=None, index_col=0, parse_dates=True, squeeze=True)
print(data.shape)
# summarize class counts
counts = data.groupby(73).size()
for i in range(len(counts)):
  percent = counts[i] / data.shape[0] * 100
  print('Class=%d, total=%d, percentage=%.3f' % (i, counts[i], percent))

运行该示例确认有2534天的数据和73个变量。

我们还可以看到数据失衡的本质，超过93%的天是非臭氧的，6%是臭氧的。

(2534, 73)
Class=0, total=2374, percentage=93.686
Class=1, total=160, percentage=6.314

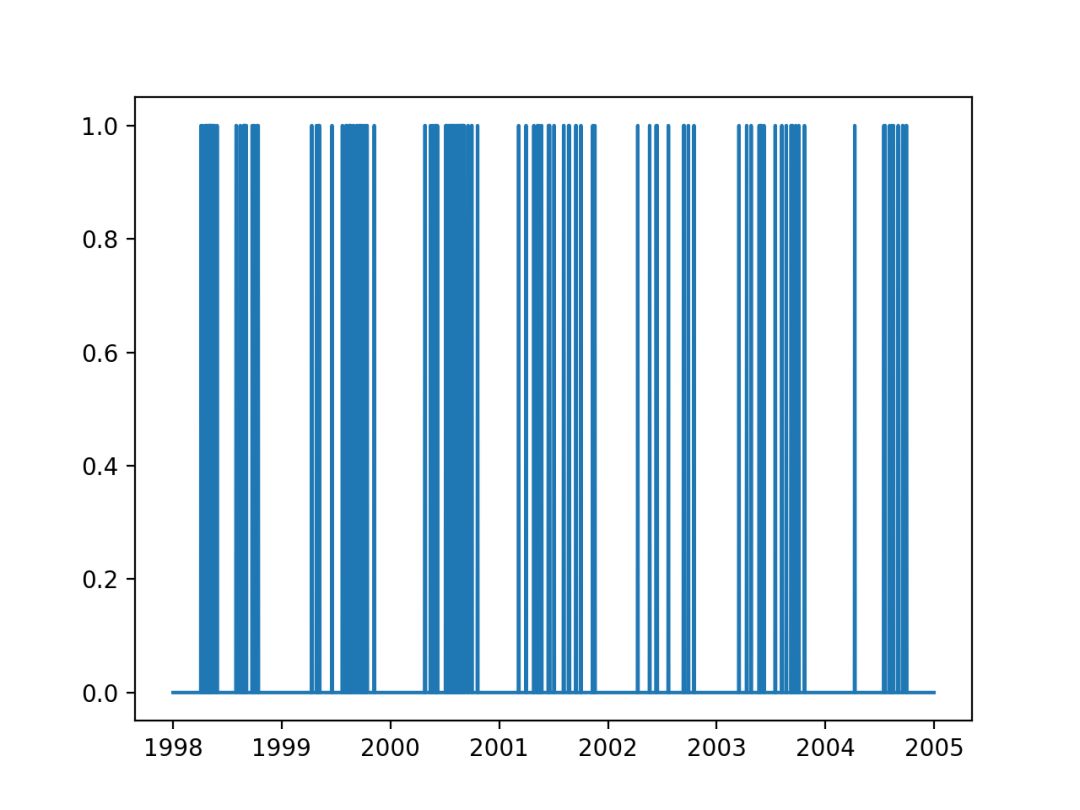
我们还可以创建输出变量的七年线图，以了解臭氧天数是否发生在一年中的任何特定时间。

# load and plot output variable
from pandas import read_csv
from matplotlib import pyplot
# load dataset
data = read_csv('eighthr.data', header=None, index_col=0, parse_dates=True, squeeze=True)
# plot the output variable
pyplot.plot(data.index, data.values[:,-1])
pyplot.show()

运行该示例将创建输出变量的七年线图。
我们可以看到，每年中期都有臭氧天集群：北半球夏季或温暖的月份。

通过简要回顾一下观察结果，我们可以得到一些关于如何准备数据的思路：

缺少数据需要处理。
最简单的框架是根据今天的观察结果预测明天的臭氧日。
温度可能与季节或一年中的时间相关，可能是一个有用的预测指标。
数据变量可能需要缩放（归一化），甚至可能需要标准化，具体取决于所选的算法。
预测概率将提供比预测类值更多的细微差别。
也许我们可以使用五年（约72％）来训练模型并在剩余的两年内测试该模型（约28％）

我们可以准备一些最小的数据。

下面的示例将加载数据集，用0.0替换缺失的观察值，将数据转为一个监督学习问题(根据今天的观察值预测明天的臭氧)，并根据两年内的大致天数将数据分成训练和测试集。

您可以探索替代缺失值的替代方法，例如估算平均值。另外，2004年是闰年，所以将数据分割成训练和测试集，不是5-2年的简单划分，但是对于本教程来说已经足够了。

# load and prepare
from pandas import read_csv
from matplotlib import pyplot
from numpy import array
from numpy import hstack
from numpy import savetxt
# load dataset
data = read_csv('eighthr.data', header=None, index_col=0, parse_dates=True, squeeze=True)
values = data.values
# replace missing observations with 0
values[values=='?'] = 0.0
# frame as supervised learning
supervised = list()
for i in range(len(values) - 1):
  X, y = values[i, :-1], values[i + 1, -1]
  row = hstack((X,y))
  supervised.append(row)
supervised = array(supervised)
# split into train-test
split = 365 * 2
train, test = supervised[:-split,:], supervised[-split:,:]
train, test = train.astype('float32'), test.astype('float32')
print(train.shape, test.shape)
# save prepared datasets
savetxt('train.csv', train, delimiter=',')
savetxt('test.csv', test, delimiter=',')

运行该示例将训练和测试集保存为CSV文件，并打印出两个数据集的维度分别是：

(1803, 73) (730, 73)

基础的预测模型

一个基础的模型可以预测每天臭氧发生的概率。

这是一种基础的方法，因为它只使用事件的基本速率之外的任何信息。在气象预报的验证中，这被称为气候预报。

我们可以从训练数据集估计臭氧日的概率，如下所示。

# load datasets
train = loadtxt('train.csv', delimiter=',')
test = loadtxt('test.csv', delimiter=',')
# estimate naive probabilistic forecast
naive = sum(train[:,-1]) / train.shape[0]

然后，我们可以在测试数据集中预测每天臭氧发生的概率。

# forecast the test dataset
yhat = [naive for _ in range(len(test))]

一旦我们有了预测，我们就可以评估它的得分。

Brier分数是评价概率预测的一种有效方法。这个分数可以被认为是预测概率(例如5%)和预期概率(0%或1%)的平均平方误差。它是测试数据集中每天发生的错误的平均值。
我们感兴趣的是使Brier分数最小化，更小的值更好，例如更小的误差。
我们可以使用scikit-learn库中的brier_score_loss()函数评估预测的Brier分数。

# evaluate forecast
testy = test[:, -1]
bs = brier_score_loss(testy, yhat)
print('Brier Score: %.6f' % bs)

一个模型要有用，它的得分必须高于上面基础模型预测的得分。
我们可以通过计算一个Brier技能分数(BSS)来说明这一点，该分数(BS)是基于基础模型预测的。
我们预计基础预测的计算BSS为0.0。接下来，我们对这个分数的最大化很感兴趣，例如BSS分数越大越好。

# calculate brier skill score
bs_ref = bs
bss = (bs - bs_ref) / (0 - bs_ref)
print('Brier Skill Score: %.6f' % bss)

下面给出了简单预测的完整示例。

# naive prediction method
from sklearn.metrics import brier_score_loss
from numpy import loadtxt
# load datasets
train = loadtxt('train.csv', delimiter=',')
test = loadtxt('test.csv', delimiter=',')
# estimate naive probabilistic forecast
naive = sum(train[:,-1]) / train.shape[0]
print(naive)
# forecast the test dataset
yhat = [naive for _ in range(len(test))]
# evaluate forecast
testy = test[:, -1]
bs = brier_score_loss(testy, yhat)
print('Brier Score: %.6f' % bs)
# calculate brier skill score
bs_ref = bs
bss = (bs - bs_ref) / (0 - bs_ref)
print('Brier Skill Score: %.6f' % bss)

通过这个例子，我们甚至可以看到臭氧日的基础概率约为7.2%。
使用基准率作为预测结果，Brier skill为0.039，而预期的Brier skill得分为0.0(忽略符号)。

0.07265668330560178
Brier Score: 0.039232
Brier Skill Score: -0.000000

我们现在准备探索一些机器学习的方法，看看我们是否可以为这个预测增加技能。
注意，最初的论文使用精确和直接回忆的方法来评估方法的技巧，这是一种令人惊讶的直接比较方法。
也许你可以探索的另一种测量方法是ROC曲线下的面积(ROC AUC)。绘制最终模型的ROC曲线将允许模型的操作者选择一个阈值，该阈值提供了真正(hit)率和假正(虚警)率之间理想的平衡水平。

集成树（Boosted Decision Tree）

预测模型

最初的论文报道了提升决策树的一些成功。

虽然我们对归纳学习者的选择了解得并不详尽，但本文表明归纳学习可以作为臭氧水平预测的一种选择方法，基于集合的概率树提供了比现有方法更好的预测(更高的查全率和精度)。

- 预测偏差随机臭氧天数：分析和解决方案，2006年。

出于以下几个原因，这并不奇怪：

提升决策树不需要任何数据缩放。
提升决策树自动进行特征选择，忽略不相关的特征。
提升决策树能预测合理校准的概率（例如，与SVM不同)。

这表明在测试问题的机器学习算法时，这将是一个很好的前提。

我们可以通过抽样检查scikit-learn库中标准集合树方法样本的性能，来快速开始，其默认配置和树数设置为100。

具体来说, 采用以下方法:

提升决策树-Bagged Decision Trees (BaggingClassifier)
扩展树(ExtraTreesClassifier)
随机梯度提升(GradientBoostingClassifier)
随机森林(RandomForestClassifier)

首先，我们必须将训练和测试数据集分割为输入(X)和输出(y)组件，以便能够适应sklearn模型。

# load datasets
train = loadtxt('train.csv', delimiter=',')
test = loadtxt('test.csv', delimiter=',')
# split into inputs/outputs
trainX, trainy, testX, testy = train[:,:-1],train[:,-1],test[:,:-1],test[:,-1]

我们还需要对基础预测的Brier分数，这样我们就可以正确计算新模型的Brier技能分数。

# estimate naive probabilistic forecast
naive = sum(train[:,-1]) / train.shape[0]
# forecast the test dataset
yhat = [naive for _ in range(len(test))]
# calculate naive bs
bs_ref = brier_score_loss(testy, yhat)

我们建立一个通用函数以此来评估一个单一的模型的技能得分。
下面定义了一个名为evaluate_once()的函数，它适合并评估给定的已定义和配置的scikit-learn模型，并返回Brier技能得分(BSS)。

# evaluate a sklearn model
def evaluate_once(bs_ref, template, trainX, trainy, testX, testy):
  # fit model
  model = clone(template)
  model.fit(trainX, trainy)
  # predict probabilities for 0 and 1
  probs = model.predict_proba(testX)
  # keep the probabilities for class=1 only
  yhat = probs[:, 1]
  # calculate brier score
  bs = brier_score_loss(testy, yhat)
  # calculate brier skill score
  bss = (bs - bs_ref) / (0 - bs_ref)
  return bss

集成树是一种随机机器学习方法。
这意味着当同一模型、相同配置、在相同的数据上训练时，他们会做出不同的预测并得到不同的结果。为了修正这个问题，我们可以多次评估一个给定的模型，比如10次，并计算每次运行的Brier技能得分(BSS)。
下面的函数将对给定的模型进行10次评估，打印平均BSS分数，并返回分数的总体进行分析。

# evaluate an sklearn model n times
def evaluate(bs_ref, model, trainX, trainy, testX, testy, n=10):
  scores = [evaluate_once(bs_ref, model, trainX, trainy, testX, testy) for _ in range(n)]
  print('>%s, bss=%.6f' % (type(model), mean(scores)))
  return scores

我们现在准备运行一组集成决策树算法。
下面列出了完整的示例。

# evaluate ensemble tree methods
from numpy import loadtxt
from numpy import mean
from matplotlib import pyplot
from sklearn.base import clone
from sklearn.metrics import brier_score_loss
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier

# evaluate a sklearn model
def evaluate_once(bs_ref, template, trainX, trainy, testX, testy):
  # fit model
  model = clone(template)
  model.fit(trainX, trainy)
  # predict probabilities for 0 and 1
  probs = model.predict_proba(testX)
  # keep the probabilities for class=1 only
  yhat = probs[:, 1]
  # calculate brier score
  bs = brier_score_loss(testy, yhat)
  # calculate brier skill score
  bss = (bs - bs_ref) / (0 - bs_ref)
  return bss

# evaluate an sklearn model n times
def evaluate(bs_ref, model, trainX, trainy, testX, testy, n=10):
  scores = [evaluate_once(bs_ref, model, trainX, trainy, testX, testy) for _ in range(n)]
  print('>%s, bss=%.6f' % (type(model), mean(scores)))
  return scores

# load datasets
train = loadtxt('train.csv', delimiter=',')
test = loadtxt('test.csv', delimiter=',')
# split into inputs/outputs
trainX, trainy, testX, testy = train[:,:-1],train[:,-1],test[:,:-1],test[:,-1]
# estimate naive probabilistic forecast
naive = sum(train[:,-1]) / train.shape[0]
# forecast the test dataset
yhat = [naive for _ in range(len(test))]
# calculate naive bs
bs_ref = brier_score_loss(testy, yhat)
# evaluate a suite of ensemble tree methods
scores, names = list(), list()
n_trees=100
# bagging
model = BaggingClassifier(n_estimators=n_trees)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('bagging')
# extra
model = ExtraTreesClassifier(n_estimators=n_trees)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('extra')
# gbm
model = GradientBoostingClassifier(n_estimators=n_trees)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('gbm')
# rf
model = RandomForestClassifier(n_estimators=n_trees)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('rf')
# plot results
pyplot.boxplot(scores, labels=names)
pyplot.show()

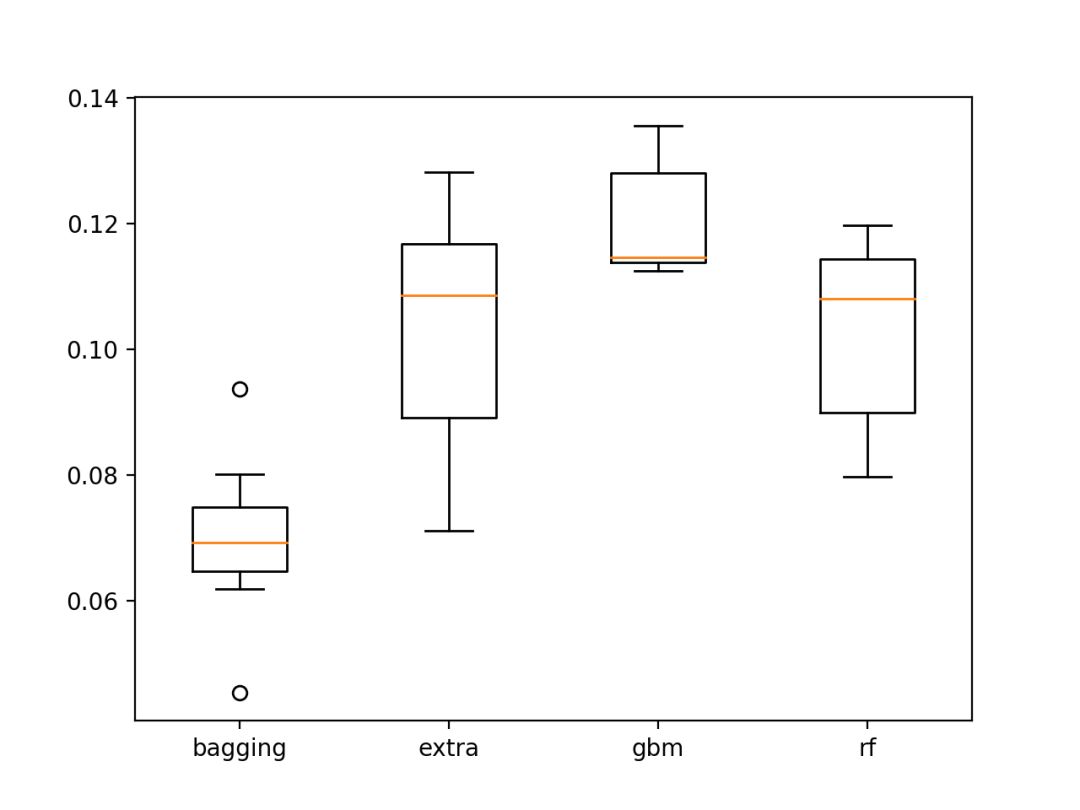
运行该代码得到每个模型在10次运行中的平均BSS。
考虑到算法的随机性，您的特定结果可能会有所不同，但趋势应该是相同的。
从平均BSS得分来看，额外的树，随机梯度提升和随机森林模型是最熟练的。

><class 'sklearn.ensemble.bagging.BaggingClassifier'>, bss=0.069762
><class 'sklearn.ensemble.forest.ExtraTreesClassifier'>, bss=0.103291
><class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>, bss=0.119803
><class 'sklearn.ensemble.forest.RandomForestClassifier'>, bss=0.102736

每个模型的得分的箱形图被绘制。
所有的模型显示BSS分数超过基础模型的预测(正面的分数)，这是非常令人鼓舞的。
扩展树、随机梯度提升和随机森林的BSS分数分布都很令人鼓舞。

调整梯度增加模型性能

考虑到随机梯度提升的优势，我们通过一些参数调整看看是否能进一步提高模型的性能。

有许多参数需要与模型进行调优，但一些用于调优模型的良好启发式方法包括:

降低学习率(learning_rate)，同时增加决策树的数量(n_estimators)。
增加决策树的最大深度(max_depth)，同时减少用于拟合树(样本)的样本数量。

我们可以根据这些原则检查一些参数，而不是网格搜索值。如果您有时间和计算资源，可以自己探索这些参数的网格搜索（编者：有时候网格搜索会带来更加优异的性能提成）。

我们将比较GBM模型的四种配置：

基线：在上一节中测试（learning_rate = 0.1，n_estimators = 100，subsample = 1.0，max_depth = 3）
学习率，具有较低的学习率和更多的树（learning_rate = 0.01，n_estimators = 500，subsample = 1.0，max_depth = 3）
深度，增加的最大树深度和较小的数据集采样（learning_rate = 0.1，n_estimators = 100，subsample = 0.7，max_depth =）
所有，所有的修改。

下面列出了完整的示例。

# tune the gbm configuration
from numpy import loadtxt
from numpy import mean
from matplotlib import pyplot
from sklearn.base import clone
from sklearn.metrics import brier_score_loss
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier

# evaluate a sklearn model
def evaluate_once(bs_ref, template, trainX, trainy, testX, testy):
  # fit model
  model = clone(template)
  model.fit(trainX, trainy)
  # predict probabilities for 0 and 1
  probs = model.predict_proba(testX)
  # keep the probabilities for class=1 only
  yhat = probs[:, 1]
  # calculate brier score
  bs = brier_score_loss(testy, yhat)
  # calculate brier skill score
  bss = (bs - bs_ref) / (0 - bs_ref)
  return bss

# evaluate an sklearn model n times
def evaluate(bs_ref, model, trainX, trainy, testX, testy, n=10):
  scores = [evaluate_once(bs_ref, model, trainX, trainy, testX, testy) for _ in range(n)]
  print('>%s, bss=%.6f' % (type(model), mean(scores)))
  return scores

# load datasets
train = loadtxt('train.csv', delimiter=',')
test = loadtxt('test.csv', delimiter=',')
# split into inputs/outputs
trainX, trainy, testX, testy = train[:,:-1],train[:,-1],test[:,:-1],test[:,-1]
# estimate naive probabilistic forecast
naive = sum(train[:,-1]) / train.shape[0]
# forecast the test dataset
yhat = [naive for _ in range(len(test))]
# calculate naive bs
bs_ref = brier_score_loss(testy, yhat)
# evaluate a suite of ensemble tree methods
scores, names = list(), list()
# base
model = GradientBoostingClassifier(learning_rate=0.1, n_estimators=100, subsample=1.0, max_depth=3)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('base')
# learning rate
model = GradientBoostingClassifier(learning_rate=0.01, n_estimators=500, subsample=1.0, max_depth=3)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('lr')
# depth
model = GradientBoostingClassifier(learning_rate=0.1, n_estimators=100, subsample=0.7, max_depth=7)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('depth')
# all
model = GradientBoostingClassifier(learning_rate=0.01, n_estimators=500, subsample=0.7, max_depth=7)
avg_bss = evaluate(bs_ref, model, trainX, trainy, testX, testy)
scores.append(avg_bss)
names.append('all')
# plot results
pyplot.boxplot(scores, labels=names)
pyplot.show()

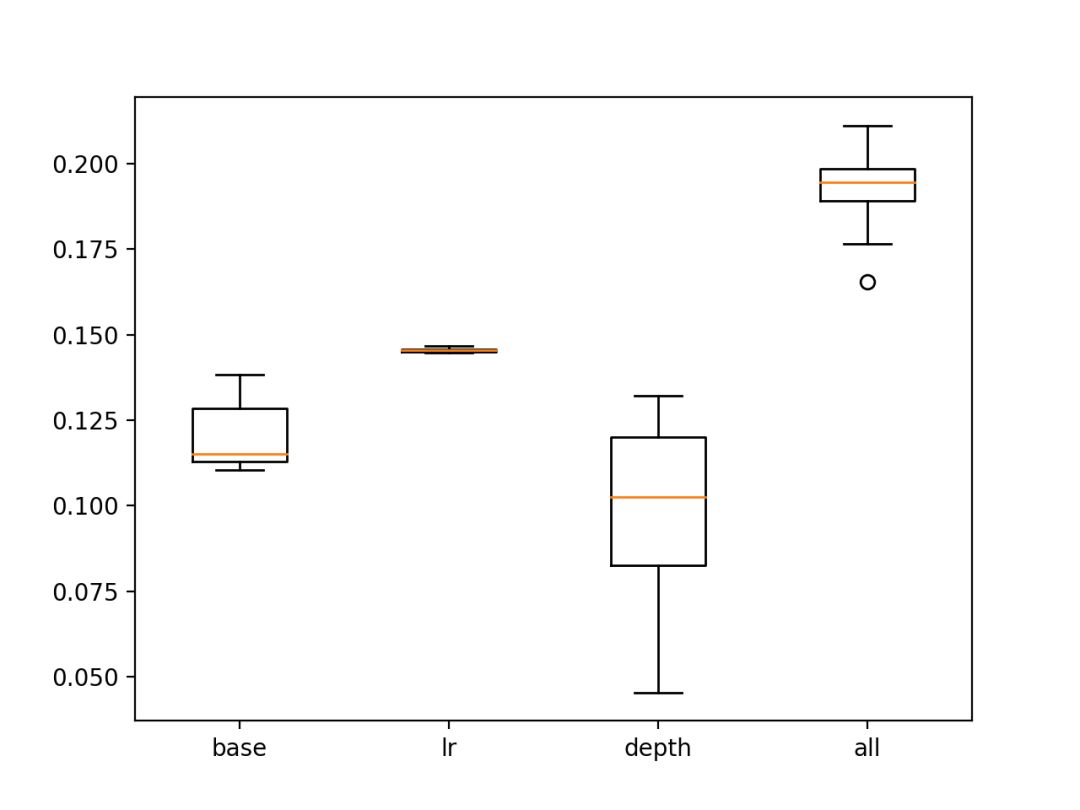
运行该代码将每个配置打印10个运行的平均每个模型的BSS得分。

结果表明，学习率和树节点数量的变化引起了对默认配置的一些提升。
结果还表明，包含每个变化的“所有”配置导致最佳平均BSS。

><class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>, bss=0.119972
><class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>, bss=0.145596
><class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>, bss=0.095871
><class 'sklearn.ensemble.gradient_boosting.GradientBoostingClassifier'>, bss=0.192175

创建了来自每个配置的BSS分数的箱形图。我们可以看到，包含所有更改的配置明显优于基线模型和其他配置组合。
也许通过对模型进行微调的参数可以进一步提高性能。

在测试集中显示BSS分数的调整的GBM模型的箱形图

如果能掌握论文中描述的参数模型以及使用它所需的数据，以便将其与最终模型的技巧进行比较，那将是一件有趣的事情。

扩展

本节列出了一些关于其他的想法，您可能希望对其进行研究。
探索模型的框架，该框架使用来自多个前几天的观察数据。
探讨使用ROC曲线图和ROC AUC测度的模型评估。
网格搜索梯度提升模型参数，并可能探索其他实现，如XGBoost。
如果你探索这些扩展中的任何一个，您可以给我来信。

进一步的阅读

如果您想深入了解这个主题，本节将提供关于这个主题的更多资源。
臭氧水平检测数据集，UCI机器学习库。
预测偏差随机臭氧日:分析与解决，2006。
预测偏差随机臭氧天数:分析，更进一步的解决方案，2008。
CAWCR验证页面
维基百科上的接收器操作特性

总结

在本教程中，您将了解如何开发一个概率预测模型来预测德克萨斯州休斯顿的空气污染。
具体来说，你学会了：
如何加载和准备臭氧日标准机器学习预测建模问题。
如何开发一个基础的预测模型，并利用Brier技能得分对预测进行评估。
如何使用决策树的集合来开发熟练的模型，并通过成功的模型的超参数调优进一步提高技巧。
所有的代码放在github上，您可以下载运行。

想要继续查看该篇文章更多代码、链接和参考文献？

戳链接：

http://www.gair.link/page/TextTranslation/1022

AI研习社每日更新精彩内容，点击文末【阅读原文】即可观看更多精彩内容：