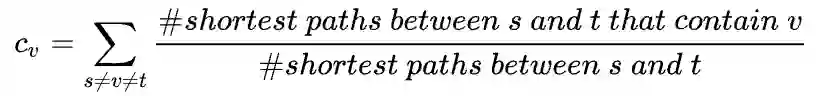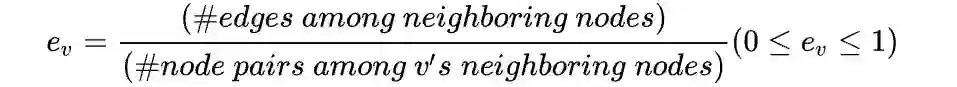传统图特征提取方法 | 节点级别的的特征（Node-level）

“强基固本，行稳致远”，科学研究离不开理论基础，人工智能学科更是需要数学、物理、神经科学等基础学科提供有力支撑，为了紧扣时代脉搏，我们推出“强基固本”专栏，讲解AI领域的基础知识，为你的科研学习提供助力，夯实理论基础，提升原始创新能力，敬请关注。

来源：知乎—葱鸭Fighting

地址：https://zhuanlan.zhihu.com/p/413568865

在传统机器学习方法的pipeline中，我们需要手动地抽取一系列特征组合成特征向量      ，并将该特征向量      与标签      作为输入来训练机器学习模型，如随机森林、SVM、前馈神经网络等等。图网络数据作为一种特殊的数据结构，其既包含了节点自身的信息，又包含了网络拓扑结构信息，那么，针对图网络结构的数据有哪些传统有效的特征提取方法？本文将结合斯坦福大学CS224W课程第四讲内容，介绍传统的基于节点水平（Node-level）的图网络数据特征提取方法。

官方油管课程视频链接：

https://youtu.be/3IS7UhNMQ3U

01

基于节点水平的特征（Node-Level Features）

传统的节点水平的图网络特征可大致分为两类：
（1）基于节点重要性的特征，衡量了某节点在网络中的重要程度，如：节点度，节点中心性度量；
（2）基于结构的特征，能够捕捉节点周围领域的拓扑属性，如：节点度，聚类系数，图元度向量（GDV，graphlet degree vector）

接下来我们对节点度，中心性，聚类系数，以及GDV等概念进行详细介绍。

1. 节点度（Node Degree）

节点度，即对节点邻居个数的计数，或是与节点连接的边的条数。当图为有向图时，节点度又可分为入度（in-degree）与出度（out-degree）。值得注意的是，节点度捕捉到的信息默认了每一个邻居节点信息都是平等的。

2. 节点中心性（Node Centrality）

节点的中心性指标有多种，它们从不同角度衡量了节点在网络中的重要程度，其中最常用的几个中心性指标分别是：特征向量中心性，中介中心性，接近中心性。

特征向量中心性（eigenvector centrality）

特征向量中心性背后的思想是：若一个节点的邻居节点的重要性高，那么它的重要性也越高。特征向量中心性计算公式      可表示为：

经过一系列的变形，以上计算方法实际上等价于如下定义：设       为网络       的邻接矩阵，通过求解特征方程       我们可以得到特征向量      ，当      为最大特征值时，第      个节点的特征向量中心性即为向量      的第      个元素。

中介中心性（betweenness centrality）

中介中心性又称为最短路径中心性（shortest-path centrality），其思想是：若一个节点在各节点对之间的最短路径上出现次数越多，则其在网络中的重要性越高。用公式可表示为：

接近中心性（closeness centrality）

接近中心性背后的思想是：若一个节点到其他所有节点的最短路径长度越小，那么它在网络中的重要性越高，以公式可表示为：

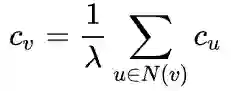
3. 聚类系数（Clustering Coefficients）

聚类系数衡量了节点的邻居节点之间的连接性高低，若它的邻居节点之间相互连接的越多，则聚类系数越大。设聚类系数为      ，计算公式表示为：

下图以带有5个节点的网络为例，展示了三种不同网络结构下节点   的聚类系数：

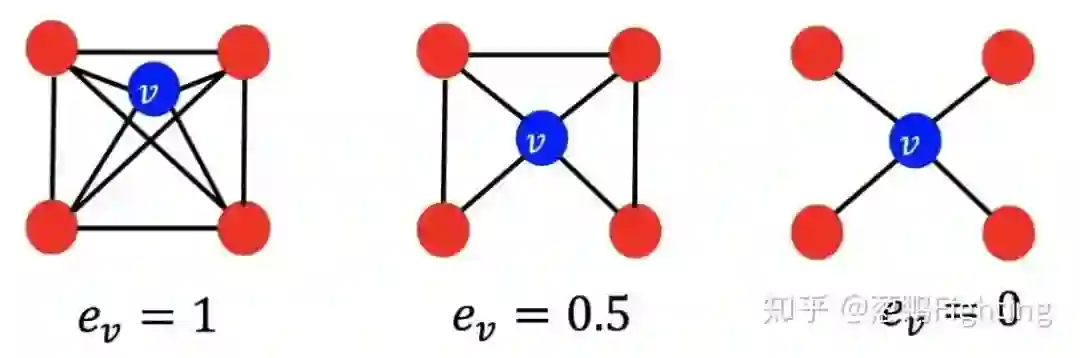
聚类系数示例图（图源自CS224W课程）

4. 图元度向量（Graphlet Degree Vector）

图元度向量对事先指定的图元（graphlet）结构进行了计数统计，从而反映了网络的结构特征。在理解图元度向量之前，我们首先要理解图元的概念。

什么是图元？ 官方给出的图元定义为“有根连通的非同构子图”。简单来说，图元就是若干个节点构成的所有可能的连通图结构，我们以课程中的示例图来进行解释。在下图中我们可以看到，当仅有两个节点时，可能的图元结构只有一种；当有三个节点时，图元结构有两种，可能是线型连接的，或是构成一个三角形（这里值得注意的是，当以不同的节点为根节点时，图元是不同的，例如       结构由于节点连接顺序不同代表了三种图元表示）；以此类推，当考虑4个或5个节点时，构成的图元结构将会更多样。

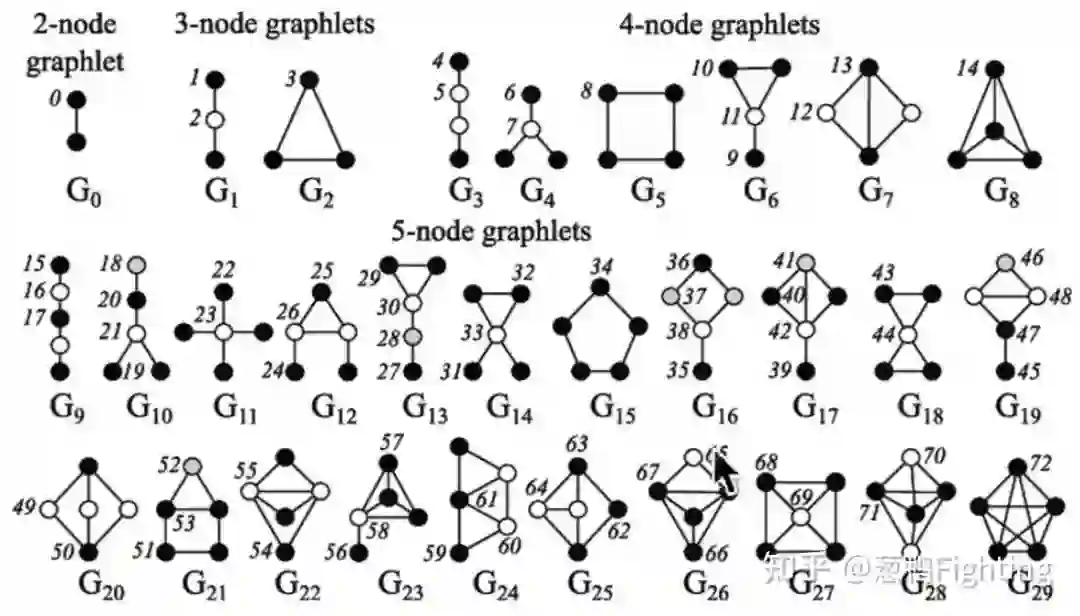
图元示例图（图源自CS224W课程）

什么是图元度向量？ 指定图元，图元度向量统计了网络中以给定节点为根的图元个数。以下图为例，网络       中的      是我们要观察的根节点，a-d指定了4种不同的图元结构，以      为根节点对网络G中四种指定的图元结构进行计数统计，各图元出现的次数分别为2,1,0,2，由此我们可以得到节点      的图元度向量为      。

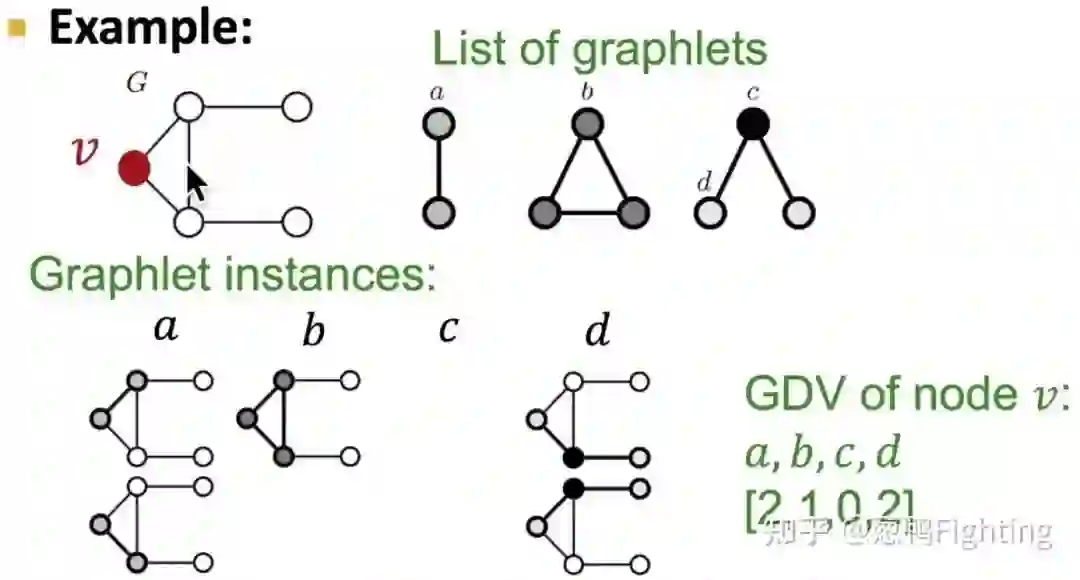
图元度向量示例（图源自CS224W课程）

02

代码实践

Python的第三方库networkx是一个非常实用的网络操作与分析工具，本部分将基于该库进行代码的实践。官方文档指路：

https://networkx.org/documentation/stable/index.html

导入第三方库

# 导入第三方网络分析库 networkx# 导入绘图库import networkx as nximport matplotlib.pyplot as pltimport pandas as pd

导入示例数据集

# 导入networkx自带的网络数据集 karate club 作为示例测试代码G = nx.karate_club_graph()
# 打印查看网络的基本信息以及可视化print(nx.info(G))nx.draw(G, pos=nx.spring_layout(G), with_labels=True)

节点度函数 G.degree(v)

# 打印查看节点度信息print("Node Degree")for v in G:    print(f"{v:4} {G.degree(v):6}")

节点中心性函数

特征向量中心性函数：nx.eigenvector_centrality(G)

中介中心性函数：nx.betweenness_centrality(G)

接近中心性函数：nx.closeness_centrality(G)

# 打印查看各种节点中心性数值# 各个中心性函数返回的是字典类型数据，key为节点index，value为中心性数值print("Node centraility")eigen_dict = nx.eigenvector_centrality(G)betw_dict = nx.betweenness_centrality(G)close_dict = nx.closeness_centrality(G)centrality_df = pd.DataFrame(    {     'eigenvector_centrality': [eigen_dict[v] for v in G],     'betweenness_centrality': [betw_dict[v] for v in G],     'closeness_centrality': [close_dict[v] for v in G],    })centrality_df

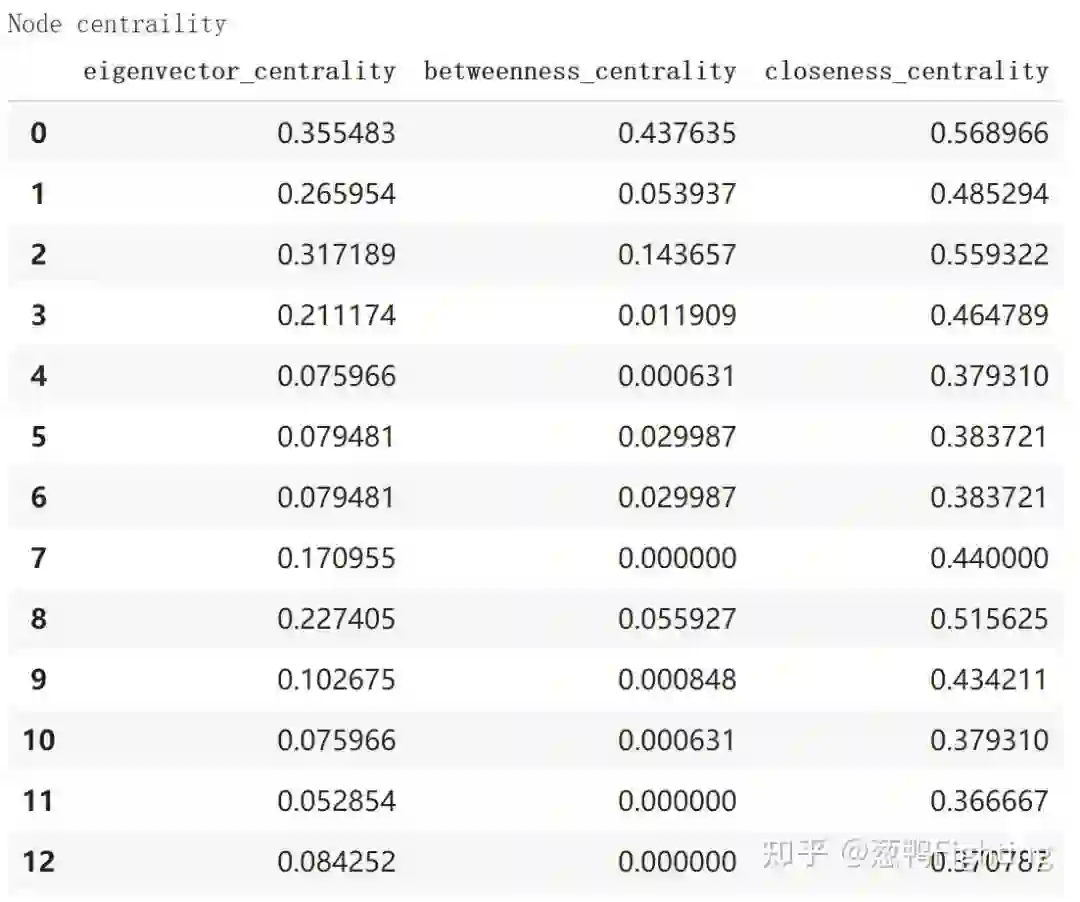
节点聚类系数函数 nx.clustering(G)

# 打印查看各种节点聚类系数# 聚类系数函数nx.clustering(G)返回的是字典类型数据，key为节点index，value为聚类系数数值print("Node Clustering Coefficients")nx.clustering(G)

运行代码会发现index为7的节点聚类系数为1，表明它的邻居节点应该呈两两之间全部相连接的状态，因此我们可以将7号节点的自我中心网络（ego-network）可视化检查看看是否符合：

ego = nx.ego_graph(G, 7)nx.draw(ego, pos=nx.spring_layout(ego), with_labels=True)

注：图元度向量（GDV）暂未找到Python代码实现，故本文内容暂不对其进行代码展示

完整代码

见google colab notebook链接：

https://colab.research.google.com/drive/1fpINHRhJmKNCJW7hVKbTZ_o1GR46Kxfq?usp=sharing

03

小结

从本节的内容我们学习到了如何从网络中手动提取节点水平的特征，包含了节点度、中心性、聚类系数，以及图元度向量等概念。试想一下，如果仅考虑节点水平的特征，我们将遗漏掉网络中重要的链接信息，因此，在下一篇文章中，我们将学习网络中基于链接水平的特征提取方法。