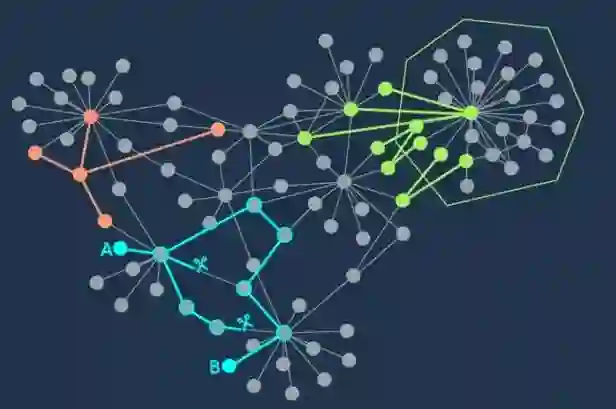
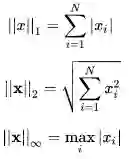如何找到距离最近的TA？

2018 年 8 月 23 日 中科院物理所

本文经「原理」（微信公众号：principia1687）授权转载，

禁止二次转载。

如果你想要开一家咖啡店，你或许会想问一个问题：附近最近的咖啡店在哪里？这个问题的答案可以帮你了解竞争对手的情况。

这是计算机科学中广泛研究的“最近邻”搜索问题的一个例子。这个问题研究的是：在给定一个数据集合和一个新的数据点的情况下，在现有数据集合中，哪个点距离新的点最近？这个问题出现在很多日常情境中，例如基因组研究、图像搜索、歌曲推荐等。

与咖啡店这个例子不同的是，最近邻问题往往非常难解答。问题的复杂性主要在于，对于不同类型的数据集，两点间距离的定义可能截然不同。

什么是距离？

我们已经完全习惯的一种定义距离的方式，就是在两点之间绘制直线，也就是我们通常所说的欧几里德距离（Euclidean distance）。

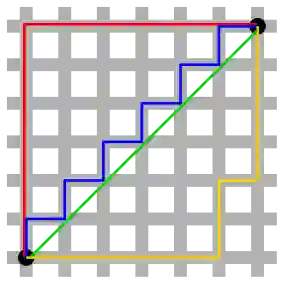
然而，在有些情况下，其他定义距离的方式更为合理。例如，在街道纵横如网格的大城市中，从一个地点到另一个地点的最短距离会是，横着向东走3公里，然后向北走4公里，而不是飞跃所有房屋的直线距离5公里。这种强迫你转90度弯的定义方式就是所谓的曼哈顿距离（Manhattan Distance）。

○ 红、蓝、黄三个线分别都曼哈顿距离，且距离都一样长（12），绿线则表示欧几里得距离。| 图片来源：Wikipedia

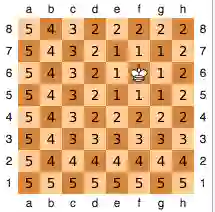
国际象棋的棋盘上，“王”从一个位置走到另一个位置需要的最少步数，被称为切比雪夫距离（Chebyshev Distance），也叫棋盘距离。

○ 国际象棋中，“王”每次可以向周围八个方向走任意步数。棋盘格中的数字表示“王”所在位置（f6）与其余位置的切比雪夫距离。| 图片来源：Wikipedia

曼哈顿距离、欧几里德距离与切比雪夫距离，分别对应于p-范数距离中的1-范数、2-范数、无穷范数。

除了从空间地理位置的角度来思考距离，还存在许多适用于其他特定类型问题的距离度量。比如说，社交网络上的两个人、两部电影、或者两个基因组之间的距离是多少？在这些例子中，“距离”是指两个事物有多大的相似度。

计算机科学中用“编辑距离”（Edit Distance）来量化比较两个字符串（例如英文单词）的差异程度。生物学家也常使用“编辑距离”，例如基因序列可被看作是A、T、C、G 四个字母组成的字符串，编辑距离可用来量化比较两个基因组的相似度：两个基因序列之间的编辑距离，就是将一个序列转换成另一个序列过程中，所需的添加、删除、插入和替换的数量。

○ 基因序列可以看作是A、T、C、G 四个字母组成的字符串。| 图片来源：Wikipedia

编辑距离和欧几里德距离是关于距离的两个完全不同的概念，其中一种定义无法被归结为另一种。这种不可通约性出现在很多距离度量对中。这意味着适用于某种距离度量的算法对另一种并不适用。这对试图开发最近邻算法的计算机科学家是极大的挑战。

寻找最近邻

寻找最近邻的标准方法，是将现有数据划分成组。例如想象一下，你的数据是草地上绵羊的位置，将成群的绵羊圈起来，如果这时草地上来了一只新绵羊，它会落入哪个圈呢？新来绵羊的最近邻在很大概率上、甚至是必然的情况下，也会在那个圈里。

然后重复这个过程，将这些圈再次划分成更小的圈，不断地对它们继续进行划分……最终，划分的圈子将只包含两个点：一个是原来就已存在的点，一个是新的点。而原来存在的点就是新点的最近邻。

这些区域的划分由算法进行绘制，好的算法能很好很快地完成划分，“好”的意思是，不太可能出现新的绵羊落入一个圈、而它的最近邻却出现在另一个圈中的情况。通过划分成组，我们希望距离近的点落入相同分区的概率高，而距离远的点落入相同分区的概率很低。

○ 最近邻搜索的方法：不断分割数据点的集合，最后添加新的点，那么，新的点（红点）及其最近邻将极有可能落入同一个小分区。| 图片来源：QuantaMagazine

多年来，计算机科学家已经提出了各种划分区域的算法。对于每个点仅由几个值定义的低维数据（如草地上绵羊的位置），算法会生成沃罗诺伊图（Voronoi diagram）来精确地求解最近邻问题。

○ 沃罗诺伊图（Voronoi diagram）：给定一系列点，平面上到任意一个给定点的距离小于到其他给定点距离的点的集合，组成一个沃罗诺伊原胞。每一个原胞为凸的多边形，原胞边界上的点到最近邻两个给定点的距离相等。图中是分别根据欧几里得距离（左）与曼哈顿距离（右）划分的沃罗诺伊图。| 图片来源：Wikipedia

对于每个点可以由成百上千个值定义的更高维度的数据，沃罗诺伊图的计算量过大。因此，计算机科学家转而用一种被称为“局部敏感散列”（locality sensitive hashing，LSH）的算法来进行划分。LSH算法会随机地进行划分，因而它的运行速度更快，但却不那么准确。也就是说，它不会精确地找到一个点的最近邻点，但能确保找到一个在实际最近邻点一定距离范围内的点。这就像是有的网站为你推荐的是“足够好”、但并非“最好”的资源。

自二十世纪九十年代代末以来，计算机科学家就提出了对特定距离度量能够近似求解最近邻问题的LSH算法。这些算法往往非常具有针对性，为一种距离度量开发的算法无法应用于另一种。对于特定的重要情形，存在非常高效针对欧几里得距离、曼哈顿距离的算法。然而，没有一个对一大类距离度量都行之有效的算法。

因此，计算机科学家只能采取迂回战术。他们通过一个名为“嵌入”（embedding）的过程，用没有高效算法的那种距离度量，覆盖有高效算法的距离度量。然而不同距离度量的拼接往往并不精确，颇有些牛头不对马嘴。在某些情况下，甚至连嵌入都根本不可能。我们真正需要的是一种解决最近邻问题的普遍方法。

最近，五位计算机科学家组成的一个团队提出了一种全新的方法来解决最近邻问题。在相继发表的两篇论文中，他们阐述了解决复杂数据最近邻问题的第一个通用方法。

论文的作者之一、麻省理工学院的计算机科学家、在开发最近邻问题算法方面很有影响力的人物Piotr Indyk说：“这是第一个使用单个算法捕捉到多种空间度量的成果。”

扩展图的阻碍

在这项新的工作中，计算机科学家不再追寻特定的最近邻算法，而是退后一步，思考一个更广泛的问题：对于一个距离度量，是什么因素阻止了最近邻算法的存在？

他们认为，这与寻找扩展图（expander graph）的最近邻问题有关，是一个非常困难的问题。扩展图是一种特定类型的图，它们由顶点和连接顶点的边组成，具有自己的距离度量。图上两点间的距离，是从一点到另一点需要经过的边的最小数目。例如，对于社交网络中表示人群连接关系的图，人与人之间的距离是他们之间的分离程度，也就是说，如果X和Y之间通过两个朋友A和B才能建立朋友关系X-A-B-Y，那么X和Y的距离就是3。

扩展图是一种特殊类型的图，有着两个看似矛盾的属性：一方面，它连接良好，要想断开这些点就必须切断许多的边；然而与此同时，大多数的点仅与极少的点连接。第二个特点导致大多数点最终彼此远离，因为低的连接度意味着在大多数点之间，都需要经过漫长、曲折的路径。

○ 扩展图的两个特点：（1）扩展图中由边连接的两个顶点是一对近邻，大多数的点仅与极少的点连接。（2）扩展图中连接良好，例如，图中有许多路径连接着A、B两点，不切断这许多边就无法使它们分离。切断点的连接意味着切断边，让近邻点分开。扩展图的特点成为了点集分区的障碍，因此，对于扩展图，最近邻搜索算法不可能实现。| 图片来源：QuantaMagazine

将连接良好，与总体来说边却很少这两个特点结合，会导致在扩展图上无法进行快速的最近邻搜索，因为在扩展图上划分点集的任何努力都可能导致近邻点的分离。

这项工作的共同作者Waingarten说：“任何在扩展图上切割点集的方式，都可能导致很多的边被切断，并使近邻点被分离。”

惊喜的结果

在2016年夏，Andoni，Nikolov，Razenshteyn和Waingarten四人就已经知道，扩展图不可能有好的最近邻算法。然而，他们真正想要证明的是，对于许多其他的距离度量（那些计算机科学家一直试图为之寻找好的算法的度量），好的最近邻算法也是不可能的。

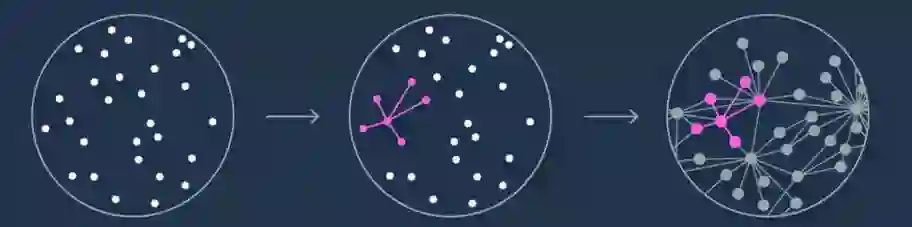
他们证明不可能有这种算法的策略是，寻找一种方法，将扩展图的距离度量嵌入其他类型的距离度量中。这样他们就可以确认，那些其他的度量具有不可行的、与扩展图类似的属性。

普林斯顿大学的数学家和计算机科学家Assaf Naor之前的工作似乎非常适合解决扩展图的问题，于是四位计算机科学家便请求Naor帮助证明扩展图嵌入多种类型距离度量的问题。很快，Naor很快就带来了答案，然而结果与四人期待的完全相反。

Naor证明，扩展图无法嵌入被称为“赋范空间”（normed space，包括欧几里德距离、曼哈顿距离等距离度量）的一类大的距离度量。有了Naor的证明做基础，他们循着逻辑链条：如果扩展图无法嵌入距离度量，而与扩展图类似的属性是良好分区的唯一障碍，那么，在赋范空间，良好的分区必然是有可能的。因而，良好的最近邻算法也必然是有可能的，即使计算机科学家还未能找到。