推荐系统论文一起读

「每周一起读」是由 PaperWeekly 发起的协同阅读小组。我们每周精选一篇优质好文，利用在线协同工具进行精读并发起讨论，在碎片化时代坚持深度阅读。目前已成立的专题小组有：Chatbot、机器翻译、知识图谱、GAN、推荐系统、QA、增强学习、多模态、自动文摘和统计学习。

Collaborative Metric Learning

http://www.cs.cornell.edu/~ylongqi/paper/HsiehYCLBE17.pdf

 论文讨论精选

blaze

[1 +d(xi;xj)2d(xi;xk)2]+,

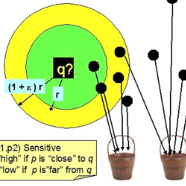
此处的 hinge loss 是如何 pushes away the impostors from the neighborhood and maintains a margin of safety 的？

edison: 此处的 push 函数输出有三种情况： 前提假设 i 和 j 是同一类别，来检测 k 是否是异常点，如果是并且对目标损失函数有影响，应加入最优化目标中。

1. 如果 i 和 k 属于同一类，则（1-yik）为 0，k 不是异常点责 push 函数失效； 

2. 如果 i 和 k 属于不同类，同时“1 +d(xi;xj)2 - d(xi;xk)2”小于等于 0，由 [z]+= max(z;0) 得 [1 +d(xi;xj)2-d(xi;xk)2] 为 0，换句话就是说 I 和 j 比 I 和 k 更相近，不影响判别 i 和 j 的距离，push 失效； 

3. 如果 i 和 k 属于不同类，同时“1 +d(xi;xj)2 - d(xi;xk)2”大于 0，由 [z]+= max(z;0) 得 [1 +d(xi;xj)2-d(xi;xk)2] 为 z，换句话就是说 I 与 j 本属于一类 pair，我们要最小话 I 和 j 的距离，由于异类 k 的影响，我也要考虑异常点带来的影响。

volador

Approximated Ranking Weight

这个地方介绍了如何计算 pairwise 样本权重，但没有找到如何从 U 个负采样样本中选择一个靠谱的负样本进行梯度更新，莫非是挑分值最高的那个？

Ttssxuan: 文中说使用 [ J/N ] 进行计算，J 是 item 的总数，N 是找到一个 inpostor 需要进行取样的次数，这样可以理解，当 N 需要的次数越少，则 weight 越大，则越容易被负例影响，LOSS 在这些 CASE 上也需要更多“关注”。

Ttssxuan

Top-K Recommendations with LSH

使用 LSH 可以加速搜索，之前在这方面也纳闷，我们经常使用的是 cosin 距离，这样就不能使用 LSH，而本文基本 euclidean 距离很好的解决这个问题，此外，直观上理解，相似、相关这类，大多应该是具有传递性的，但在 cosin 距离中，这方面几乎不能体现。

volador: 在用分解模型做 pairwise 推荐时候，基本上都是基于内积计算。

MorrisLee: Hi，请问这里具体是怎样去做推荐的呢？我只是明白 loss function 的意思，对它的输出 $u^{}$ 和 $v^()$，之后是再用一些相似性度量的方法？还是？

volador: 要看你在目标函数里面是怎么 user-item 的相似度了，这篇文章用了欧几里得距离，那么在计算得分的时候最好也采用欧几里得距离，用其他的度量方法估计对效果影响会非常大。

volador

Weighted Approximate-Rank Pairwise (WARP)

其实 WARP 的原文是这么计算权重 w 的。首先 w 是依赖正样本商品 i 排序位置的函数，核心部分就落在了正样本商品 i 的排序位置估计上面。假设在第 t 次迭代的时候商品 i 的排序位置为 r_i, 那么采样到排序位置比 i 高的负样本概率就为 lambda = r_i / |I|。这个采样过程可以理解成一个几何分布，进行很多次试验，找到这么一个排序位置比 i 高的负样本的期望次数为 1 / lambda。但本文直接采样一批商品，然后估计 lambda = M / U。

ben: Thanks, 非常有趣的问题，暂且不管本文的处理。真正的权重 w 和真实的排序位置有关这非常合理，问题就是于如何估计真实的排序位置 r_ir i 的问题，因为真实的 rank 是未知的。一个合理的步骤是利用上一次的结果 \hat{r}_i r ^  i 计算 weight，利用新的 weight 估计新的 \hat{r}_i r ^  i 直到收敛。

volador: 这里其实并不 care 真实的排序，w 只是定义的一种 pairwise loss，假设前提是 scoring function 的输出要让正样本的排序位置要比负样本的高，正样本的排序靠后就会产生 loss，越靠后 loss 就越大。r+ir+i 是可以直接通过暴力排序得到的，但这个计算量太大了，所以就有了采样估计的思路了。

ben: 我觉得我们必须讲清楚我们的 Goal 是什么，如果这个 goal 只是要把 S 这个集合区分开来，那我完全同意你的观点，甚至 w 都可以不用，直接 SVM classification 就可以做到这一点。 但是对于这个例子，我不这么认为，即使在 S 集合里面的 item 难道就没有 weight 的区别了吗。我觉得是有的，而且和真实的 rank 有关。直观上来看，我们在被推荐的时候，总是更多地去关注前几名被推荐的 item。这一点在普遍的 ranking 的指标 MAP, NDCG 都有体现。所以我还是认为这个权重是和真实的 rank 有关的。 你最后说的 r_ir i 用暴力来获得，我不是特别理解。

volador: 我以为你是在针对这篇工作来讨论，你可以看下 Section 3.1 的假设是希望在只有隐含反馈数据的情况下学习一个排序函数。集合里面的 item 肯定是有区别的，但这篇论文讨论的场景并没有什么 rating 之类的显性反馈。这里并非是完全的 classification，也没有什么 feature。你可以对所有商品进行打分，然后排序得到 r_i。

edison: ben 的点是正确的，wij 的确和真 rank 有关，原文中还有一处说 rank_ij 就是在 user 的 S 集合计算而来，而 rank_ij 决定 wij 的输出。

masker: 你把原文 WARP 的引用过来的过程可能被它吸引去了一部分精力，原文是 sample 一个负例，这里是考虑正例之间的权重。

想和我们一起研读优质paper？

点击「阅读原文」提交内测申请，我们将在 48 小时内完成审核并和您取得联系。

关于PaperWeekly

PaperWeekly是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事AI领域，欢迎在公众号后台点击「交流群」，小助手将把你带入PaperWeekly的交流群里。

点击 |  阅读原文 | 进行报名