系列教程GNN-algorithms之四：《Inductive Learning 大神—GraphSAGE》

2020 年 8 月 6 日 专知

【导读】在GCN如日中天的时候，我们不忽略它的巨大缺陷，即无法快速表征新的节点，这限制了它的应用场景。GraphSAGE属于归纳式学习方法，通过学习聚合函数来学习图的拓扑结构，进而方便的得到新节点的特征，所得节点特征会根据邻居关系变化而变化。本文将以MaxPooling聚合方法为例手把手教大家构建GraphSAGE模型。

系列教程《GNN-algorithms》

本文为系列教程《GNN-algorithms》中的内容，该系列教程不仅会深入介绍GNN的理论基础，还结合了TensorFlow GNN框架tf_geometric对各种GNN模型（GCN、GAT、GIN、SAGPool等）的实现进行了详细地介绍。本系列教程作者王有泽（https://github.com/wangyouze）也是tf_geometric框架的贡献者之一。

系列教程《GNN-algorithms》Github链接：

https://github.com/wangyouze/GNN-algorithms

TensorFlow GNN框架tf_geometric的Github链接：

https://github.com/CrawlScript/tf_geometric

前序讲解：

系列教程GNN-algorithms之一：《图卷积网络（GCN）的前世今生》

系列教程GNN-algorithms之二：《切比雪夫显神威—ChebyNet》

系列教程GNN-algorithms之三：《将图卷积简化进行到底—SGC》

前言

本教程将带你一起在PPI（蛋白质网络）数据集上用Tensorflow搭建GraphSAGE框架中的MaxPooling聚合模型实现有监督下的图节点标签预测任务。完整代码可以在Github中进行下载：

https://github.com/CrawlScript/tf_geometric/blob/master/demo/demo_graph_sage.py

GraphSAGE简介

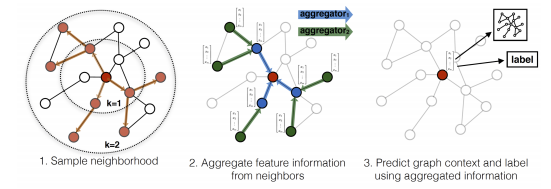
GraphSAGE是一种在超大规模图上利用节点的属性信息高效产生未知节点特征表示的归纳式学习框架。GraphSAGE可以被用来生成节点的低维向量表示，尤其对于是那些具有丰富节点属性的Graph效果显著。目前大多数的框架都是直推式学习模型，也就是说只能够在一张固定的Graph上进行表示学习，这些模型既不能够对那些在训练中未见的节点进行有效的向量表示，也不能够跨图进行节点表示学习。GraphSAGE作为一种归纳式的表示学习框架能够利用节点丰富的属性信息有效地生成未知节点的特征表示。

GraphSAGE的核心思想是通过学习一个对邻居节点进行聚合表示的函数来产生中心节点的特征表示而不是学习节点本身的embedding。它既可以进行有监督学习也可以进行无监督学习，GraphSAGE中的聚合函数有以下几种：

Mean Aggregator
Mean 聚合近乎等价于GCN中的卷积传播操作，具体来说就是对中心节点的邻居节点的特征向量进行求均值操作，然后和中心节点特征向量进行拼接，中间要经过两次非线性变换。
GCN Aggregator
GCN的归纳式学习版本
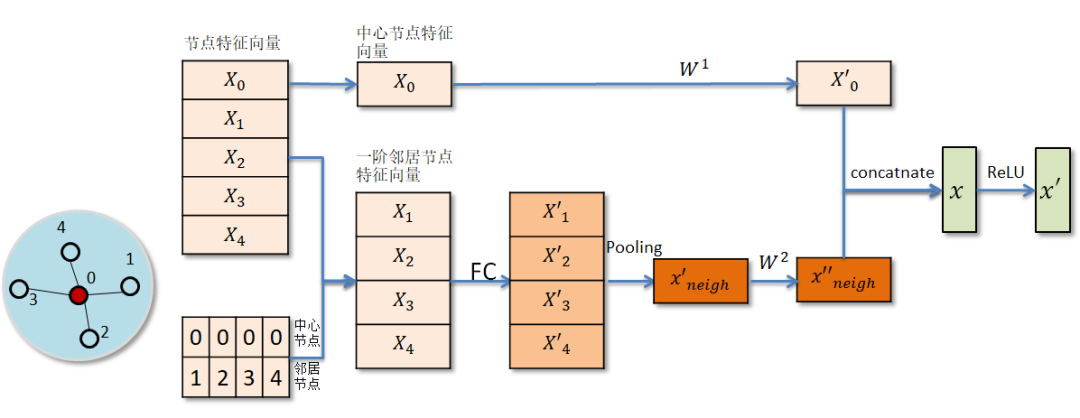
Pooling Aggregator

先对中心节点的邻居节点表示向量进行一次非线性变换，然后对变换后的邻居表示向量进行池化操作（mean pooling或者max pooling），最后将pooling所得结果与中心节点的特征表示分别进行非线性变换，并将所得结果进行拼接或者相加从而得到中心节点在该层的向量表示。
LSTM Aggregator
LSTM Aggregator 将中心节点的邻居节点随机打乱作为输入序列，将所得向量表示与中心节点的向量表示分别经过非线性变换后拼接得到中心节点在该层的向量表示。LSTM本身是用于序列数据，而邻居节点没有明显的序列关系，因此输入到LSTM中的邻居节点需要随机打乱顺序。

下面我们将以MaxPooling聚合方法为例构建GraphSAGE模型进行有监督学习下的分类任务。

教程中完整的代码链接：
https://github.com/CrawlScript/tf_geometric/blob/master/demo/demo_graph_sage.py
论文地址：https://arxiv.org/pdf/1706.02216.pdf

教程目录

数据集PPI
开发环境
max_pooling_graph_sage的具体实现
GraphSAGE的训练
GraphSAGE的评估

PPI数据集

PPI(Protein-protein interaction networks)数据集由24个对应人体不同组织的图组成。其中20个图用于训练，2个图用于验证，2个图用于测试。平均每张图有2372个节点，每个节点有50个特征。测试集中的图与训练集中的图没有交叉，即在训练阶段测试集中的图是不可见的。每个节点拥有多种标签，标签的种类总共有121种。

开发环境

操作系统: Windows / Linux / Mac OS
Python 版本: >= 3.5
依赖包:

tf_geometric（一个基于Tensorflow的GNN库）

根据你的环境（是否已安装TensorFlow、是否需要GPU）从下面选择一条安装命令即可一键安装所有Python依赖:

	pip install -U tf_geometric # 这会使用你自带的TensorFlow，注意你需要tensorflow/tensorflow-gpu >= 1.14.0 or >= 2.0.0b1

	pip install -U tf_geometric[tf1-cpu] # 这会自动安装TensorFlow 1.x CPU版

	pip install -U tf_geometric[tf1-gpu] # 这会自动安装TensorFlow 1.x GPU版

	pip install -U tf_geometric[tf2-cpu] # 这会自动安装TensorFlow 2.x CPU版

	pip install -U tf_geometric[tf2-gpu] # 这会自动安装TensorFlow 2.x GPU版

教程使用的核心库是tf_geometric，一个基于TensorFlow的GNN库。tf_geometric的详细教程可以在其Github主页上查询：

https://github.com/CrawlScript/tf_geometric

max_pooling_graph_sage的具体实现

MaxPooling 聚合函数是一个带有max-pooling操作的单层神经网络。我们首先传递每个中心节点的邻居节点向量到一个非线性层中。由于我们的tf_geometric是基于边表结构进行相关Graph操作，所以我们先通过tf.gather转换得到所有节点的邻居节点的特征向量组成的特征矩阵。

    row, col = edge_index    repeated_x = tf.gather(x, row)    neighbor_x = tf.gather(x, col)

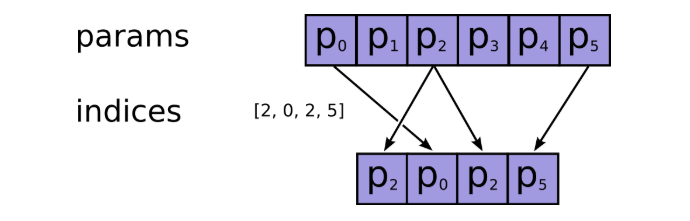
row是Graph中的源节点序列，low是Graph中的目标节点序列，x是Graph中的节点特征矩阵。tf.gather是根据节点序列从节点特征矩阵中选取对应的节点特征堆叠形成所有邻居节点组成的特征矩阵。tf.gather的具体操作如下：

tf.gather：https://www.tensorflow.org/api_docs/python/tf/gather

得到加权后的邻居节点特征向量

neighbor_x = gcn_mapper(repeated_x, neighbor_x, edge_weight=edge_weight)

在进行max-pooling操作之前将所有邻居节点的特征向量输入全连接网络计算邻居节点的特征表示。（将MLP看做是一组函数）

   neighbor_x = dropout(neighbor_x)    h = neighbor_x @ mlp_kernel    if mlp_bias is not None:        h += mlp_bias
    if activation is not None:        h = activation(h)

对邻居节点特征向量进行max-pooling操作，然后将所得向量与经过变换的中心节点特征向量拼接输出。一个理想的聚合方法就应该是简单，可学习且对称的。换句话说，一个理想的aggregator应该学会如何聚合邻居节点的特征表示，并对邻居节点的顺序不敏感，同时不会造成巨大的训练开销。

    reduced_h = max_reducer(h, row, num_nodes=len(x))    reduced_h = dropout(reduced_h)    x = dropout(x)
    from_neighs = reduced_h @ neighs_kernel    from_x = x @ self_kernel    output = tf.concat([from_neighs, from_x], axis=1)    if bias is not None:        output += bias
    if activation is not None:        output = activation(output)
    if normalize:        output = tf.nn.l2_normalize(output, axis=-1)
    return output

构建模型

导入相关库
本教程使用的核心库是tf_geometric，借助这个GNN库我们可以方便的对数据集进行导入，预处理图数据以及搭建图神经网络。另外我们还引用了tf.keras.layers中的Dropout用来缓解过拟合以及sklearn中的micro f1_score函数作为评价指标。

# coding=utf-8import osimport tensorflow as tffrom tensorflow import kerasimport numpy as npfrom tf_geometric.layers.conv.graph_sage import  MaxPoolingGraphSagefrom tf_geometric.datasets.ppi import PPIDatasetfrom sklearn.metrics import f1_scorefrom tqdm import tqdmfrom tf_geometric.utils.graph_utils import RandomNeighborSampler

加载数据集，我们使用tf_geometric自带的PPI数据集。tf_geometric提供了非常简单的图数据构建接口，只需要传入简单的Python数组或Numpy数组作为节点特征和邻接表就可以构建自己的数据集。示例请看GIN：
```
train_graphs, valid_graphs, test_graphs = PPIDataset().load_data()
```
我们使用tf_geometric自带的PPI数据集，返回划分好的训练集(20)，验证集(2)，测试集(2)。
对Graph中的每个节点的邻居节点进行采样
由于每个节点的邻居节点的数目不一，出于计算效率的考虑，我们对每个节点采样一定数量的邻居节点作为之后聚合领域信息时的邻居节点。设定采样数量为num_sample，如果邻居节点的数量大于num_sample，那我们采用无放回采样。如果邻居节点的数量小于num_sample，我们采用有放回采样，直到所采样的邻居节点数量达到num_sample。RandomNeighborSampler提前对每张图进行预处理，将相关的图信息与各自的图绑定。
```
# traverse all graphsfor graph in train_graphs + valid_graphs + test_graphs:    neighbor_sampler = RandomNeighborSampler(graph.edge_index)    graph.cache["sampler"] = neighbor_sampler
```
需要注意的是，由于模型可能会同时作用在多个图上，为了保证每张图的邻居节点在抽样结束之后不发生混淆，我们将抽样结果与每个Graph对象绑定在一起，即将抽样信息保存在“cache"这个缓存字典之中。

采用两层MaxPooling聚合函数来聚合Graph中邻居节点蕴含的信息。

graph_sages = [    MaxPoolingGraphSage(units=128, activation=tf.nn.relu),    MaxPoolingGraphSage(units=128, activation=tf.nn.relu)]
fc = tf.keras.Sequential([    keras.layers.Dropout(0.3),    tf.keras.layers.Dense(num_classes)])
num_sampled_neighbors_list = [25, 10]
def forward(graph, training=False):    neighbor_sampler = graph.cache["sampler"]    h = graph.x    for i, (graph_sage, num_sampled_neighbors) in enumerate(zip(graph_sages, num_sampled_neighbors_list)):        sampled_edge_index, sampled_edge_weight = neighbor_sampler.sample(k=num_sampled_neighbors)        h = graph_sage([h, sampled_edge_index, sampled_edge_weight], training=training)
    h = fc(h, training=training)
    return h

两层MaxPooling聚合函数的邻居节点采样数目分别为25和10。之前我们已经通过RandomNeighborSampler为每张图处理好了相关的图结构信息，现在只需要根据每层的抽样数目num_sampled_neighbors分别进行抽样（neighbor_sample.sample()）。将抽样所得的边sampled_edge_indext，边的权重sampled_edge_weights以及节点的特征向量x输入到GrapSAGE模型中。由于Dropout层在训练和预测阶段的状态不同，为此，我们通过参数training来决定是否需要Dropout发挥作用。

GraphSAGE训练

模型的训练与其他基于Tensorflow框架的模型训练基本一致，主要步骤有定义优化器，计算误差与梯度，反向传播等。需要注意的是，训练阶段forward函数的参数training=True，即此时模型执行Dropout操作。当预测阶段，输入为valid_graphs或者test_graphs时，forward的参数training=False，此时不执行Dropout操作。GraphSAGE论文用模型在第10轮训练后的表现来评估模型，因此这里我们将epoches设置为10。

optimizer = tf.keras.optimizers.Adam(learning_rate=1e-2)
for epoch in tqdm(range(10)):    for graph in train_graphs:        with tf.GradientTape() as tape:            logits = forward(graph, training=True)            loss = compute_loss(logits, tape.watched_variables())
        vars = tape.watched_variables()        grads = tape.gradient(loss, vars)        optimizer.apply_gradients(zip(grads, vars))
    if epoch % 1 == 0:        valid_f1_mic = evaluate(valid_graphs)        test_f1_mic = evaluate(test_graphs)        print("epoch = {}\tloss = {}\tvalid_f1_micro = {}".format(epoch, loss, valid_f1_mic))        print("epoch = {}\ttest_f1_micro = {}".format(epoch, test_f1_mic))

计算模型Loss

由于PPI数据集中的每个节点具有多个标签，属于多标签，多分类任务，因此我们选用sigmoid交叉熵函数。这里的logits是模型对节点标签的预测结果，graph.y是图节点的真实标签。为了防止模型出现过拟合现象，我们对模型的参数使用L2正则化。

def compute_loss(logits, vars):    losses = tf.nn.sigmoid_cross_entropy_with_logits(        logits=logits,        labels=tf.convert_to_tensor(graph.y, dtype=tf.float32)    )
    kernel_vals = [var for var in vars if "kernel" in var.name]    l2_losses = [tf.nn.l2_loss(kernel_var) for kernel_var in kernel_vals]
    return tf.reduce_mean(losses) + tf.add_n(l2_losses) * 1e-5

GraphSAGE评估

我们使用F1 Score来评估MaxPoolingGraphSAGE聚合邻居节点信息进行分类任务的性能。将测试集中的图(训练阶段unseen)输入到经过训练的MaxPoolingGraphSAGE得到预测结果，最后预测结果与其对应的labels转换为一维数组，输入到sklearn中的f1_score方法，得到F1_Score。

def evaluate(graphs):    y_preds = []    y_true = []
    for graph in graphs:        y_true.append(graph.y)        logits = forward(graph)        y_preds.append(logits.numpy())
    y_pred = np.concatenate(y_preds, axis=0)    y = np.concatenate(y_true, axis=0)
    mic = calc_f1(y, y_pred)
    return mic

运行结果

epoch = 1  loss = 0.5231980085372925  valid_f1_micro = 0.45228990047917433epoch = 1  test_f1_micro = 0.45506719065662915 27%|██▋       | 3/11 [01:11<03:12, 24.11s/it]epoch = 2  loss = 0.5082718729972839  valid_f1_micro = 0.4825462475136504epoch = 2  test_f1_micro = 0.4882603340749235epoch = 3  loss = 0.49998781085014343  valid_f1_micro = 0.4906942451215627epoch = 3  test_f1_micro = 0.502555249743498 45%|████▌     | 5/11 [01:55<02:16, 22.79s/it]epoch = 4  loss = 0.4901132583618164  valid_f1_micro = 0.5383310665693446epoch = 4  test_f1_micro = 0.5478608072643453epoch = 5  loss = 0.484283983707428  valid_f1_micro = 0.5455753374297568epoch = 5  test_f1_micro = 0.5516753473281046 64%|██████▎   | 7/11 [02:41<01:31, 22.95s/it]epoch = 6  loss = 0.4761819541454315  valid_f1_micro = 0.5417373280572828epoch = 6  test_f1_micro = 0.5504290907273931 73%|███████▎  | 8/11 [03:03<01:08, 22.71s/it]epoch = 7  loss = 0.46836230158805847  valid_f1_micro = 0.5720065995217665epoch = 7  test_f1_micro = 0.5843164717276317 82%|████████▏ | 9/11 [03:24<00:44, 22.34s/it]epoch = 8  loss = 0.4760943651199341  valid_f1_micro = 0.5752257074185534epoch = 8  test_f1_micro = 0.5855495700393325 91%|█████████ | 10/11 [03:47<00:22, 22.34s/it]epoch = 9  loss = 0.461212694644928  valid_f1_micro = 0.5812645586399496epoch = 9  test_f1_micro = 0.5930584548044271100%|██████████| 11/11 [04:08<00:00, 22.61s/it]epoch = 10  loss = 0.4568028450012207  valid_f1_micro = 0.5833869662874881epoch = 10  test_f1_micro = 0.5964539684054789