深度学习中7种最优化算法的可视化与理解

关注“深度学习自然语言处理”，一起学习一起冲鸭！

设为星标，第一时间获取更多干货

来自：Python遇见机器学习

本文仅作学术分享，若侵权，请联 系后台删文处理

来自 https://zhuanlan.zhihu.com/p/41799394

本文旨在优化一维函数，实际上模型参数有数百万维以上，差距很大，因此本文最好作为辅助法的理解，而非对算法优劣的判断依据。

在深度学习中，有很多种优化算法，这些算法需要在极高维度（通常参数有数百万个以上）也即数百万维的空间进行梯度下降，从最开始的初始点开始，寻找最优化的参数，通常这一过程可能会遇到多种的情况，诸如：

1、提前遇到局部最小值从而卡住，再也找不到全局最小值了。

2、遇到极为平坦的地方：“平原”，在这里梯度极小，经过多次迭代也无法离开。同理，鞍点也是一样的，在鞍点处，各方向的梯度极小，尽管沿着某一个方向稍微走一下就能离开。

3、“悬崖”，某个方向上参数的梯度可能突然变得奇大无比，在这个地方，梯度可能会造成难以预估的后果，可能让已经收敛的参数突然跑到极远地方去。

为了可视化&更好的理解这些优化算法，我首先拼出了一个很变态的一维函数：

其导数具有很简单的形式：

具体长得像：

具有悬崖和大量的局部最小值，足以模拟较为复杂的优化情况了。

算法1：纯粹的梯度下降法

该算法很简单，表述如下：

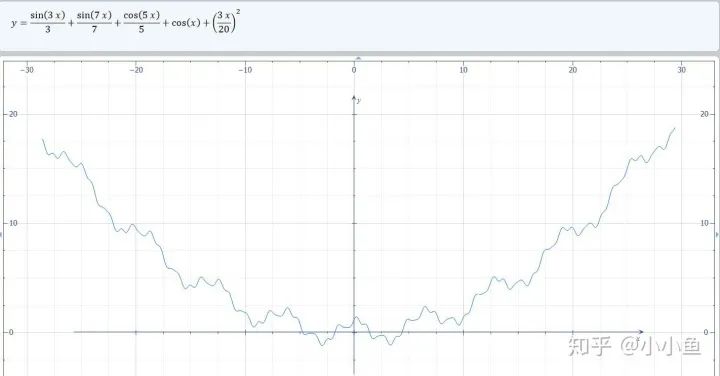
          首先给出学习率lr，初始x                   while True：                  x = x - lr*df/dx

根据学习率的不同，可以看到不同的效果。学习率过小，卡在局部极小值，学习率过大，压根不收敛。

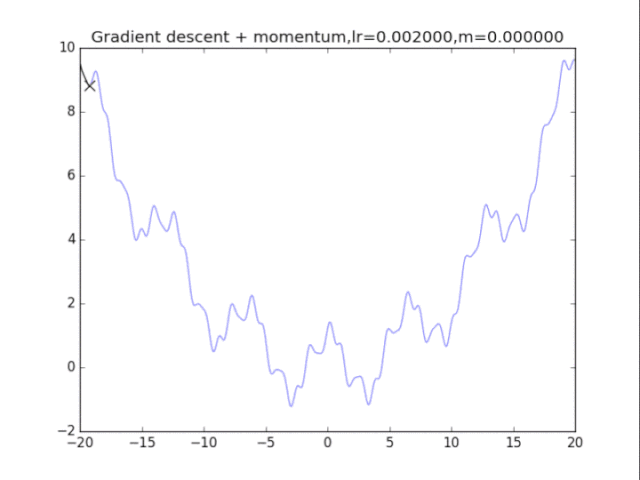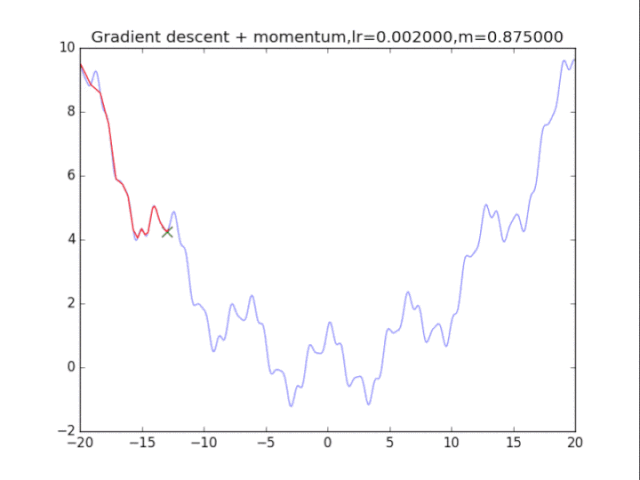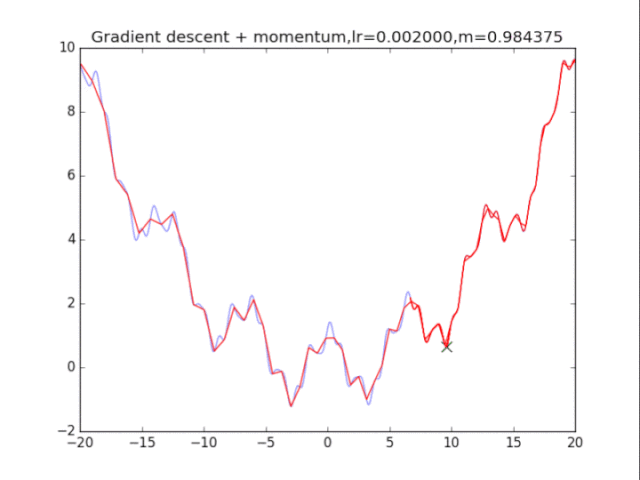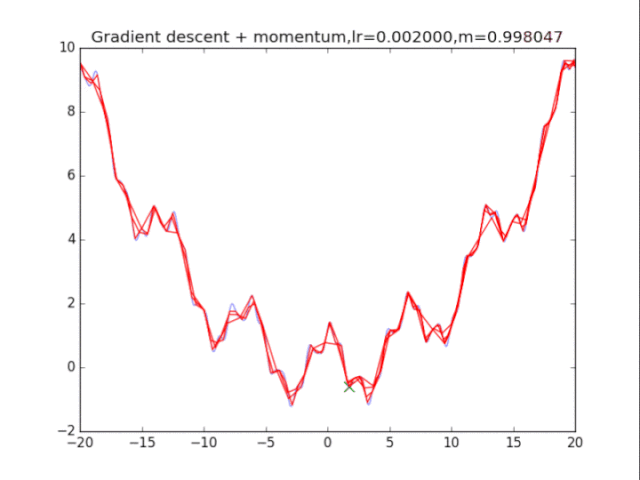
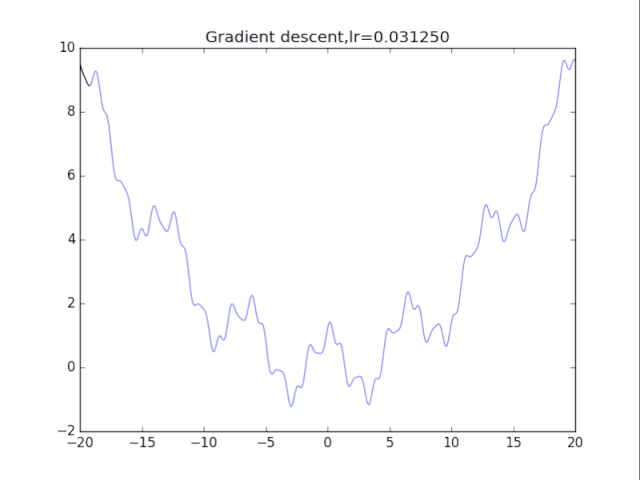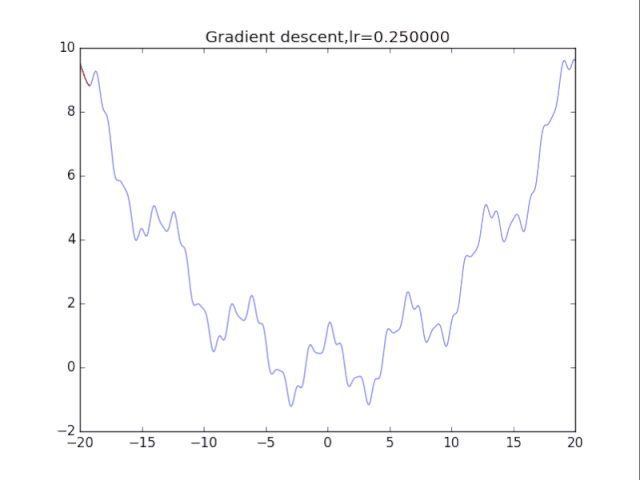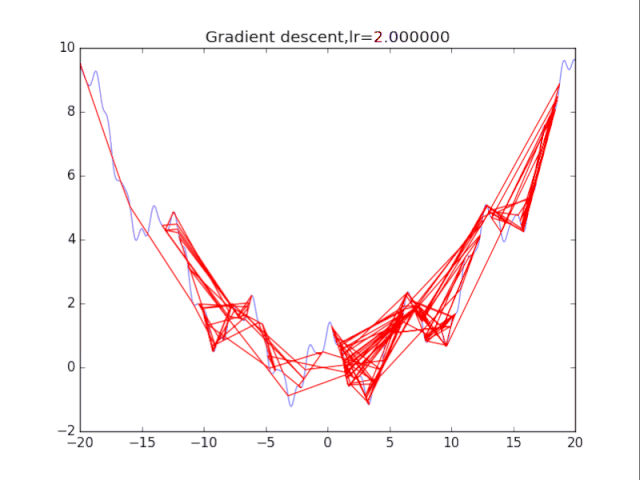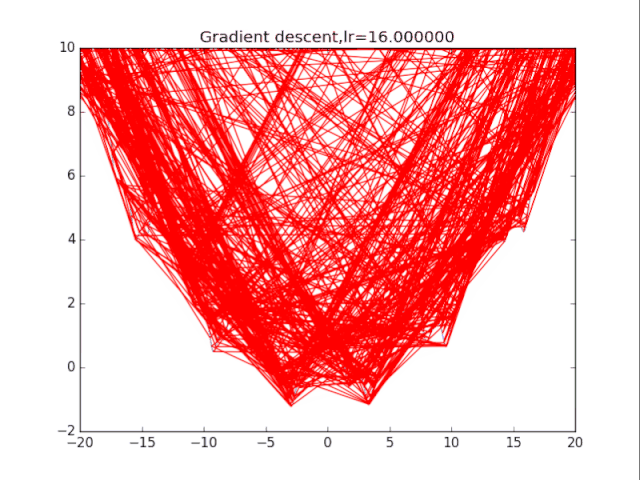梯度下降法

算法2：梯度下降法+动量

算法在纯粹的梯度下降法之上，外加了梯度，从而记录下了历史的梯度情况，从而减轻了卡在局部最小值的危险，在梯度=0的地方仍然会有一定的v剩余，从而在最小值附近摇摆。

       首先给出学习率lr，动量参数m       初始速度v=0,初始x       while True：                  v = m * v - lr * df/dx                  x += v

下面可以看图：

梯度下降+动量， lr=0.05

梯度下降+动量， lr=0.01

梯度下降+动量， lr=0.002

从中我们可以看出：

1、lr越小越稳定，太大了很难收敛到最小值上，但是太小的话收敛就太慢了。

2、动量参数不能太小，0.9以上表现比较好，但是又不能太大，太大了无法停留在最小值处。

算法3：AdaGrad算法

AdaGrad算法的思想是累计历史上出现过的梯度（平方），用积累的梯度平方的总和的平方根，去逐元素地缩小现在的梯度。某种意义上是在自行缩小学习率，学习率的缩小与过去出现过的梯度有关。

缺点是：刚开始参数的梯度一般很大，但是算法在一开始就强力地缩小了梯度的大小，也称学习率的过早过量减少。

算法描述：

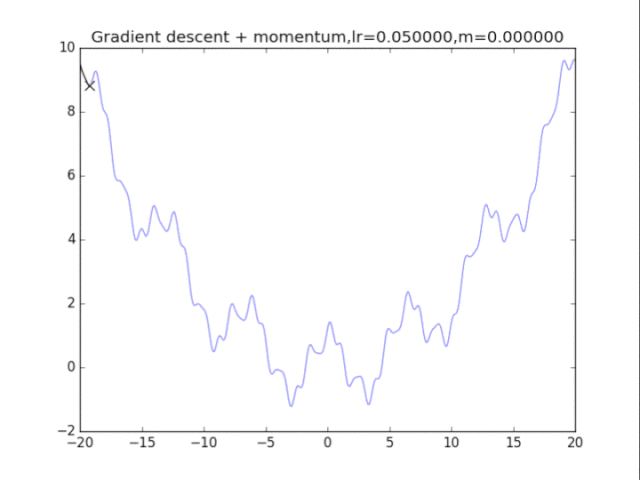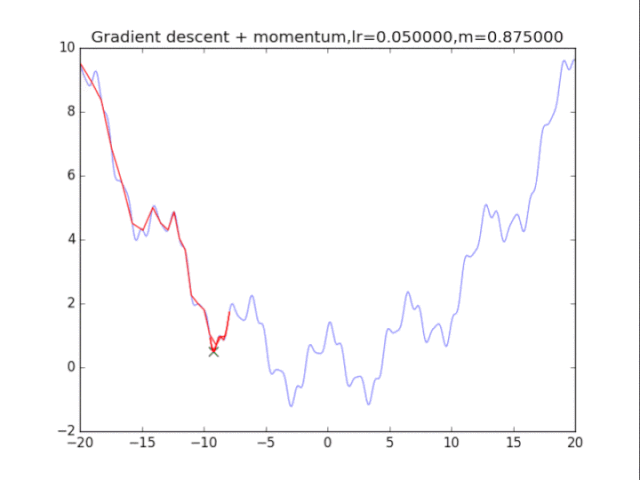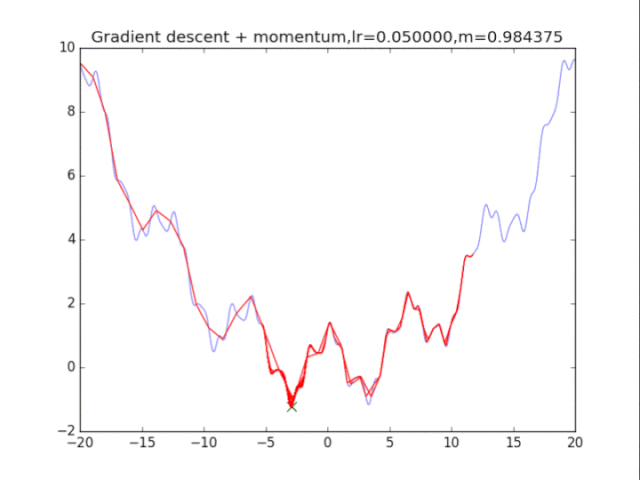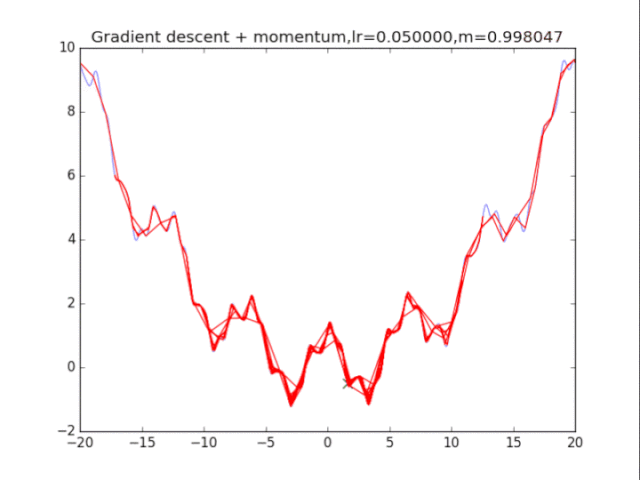
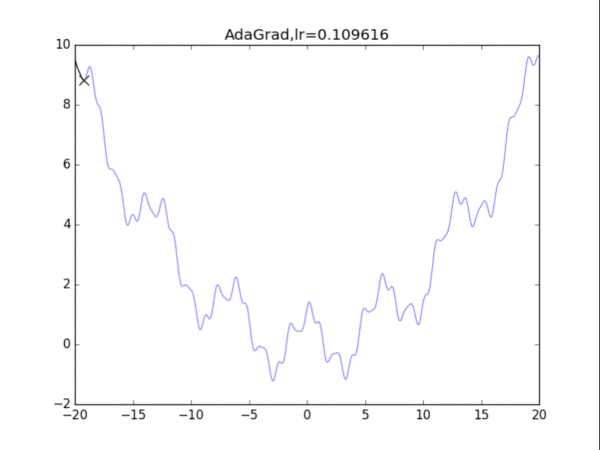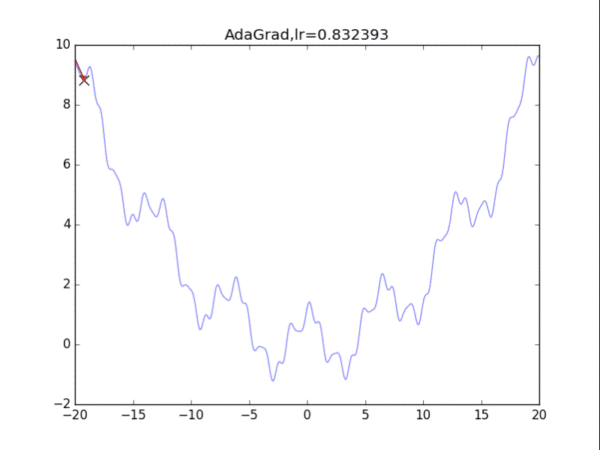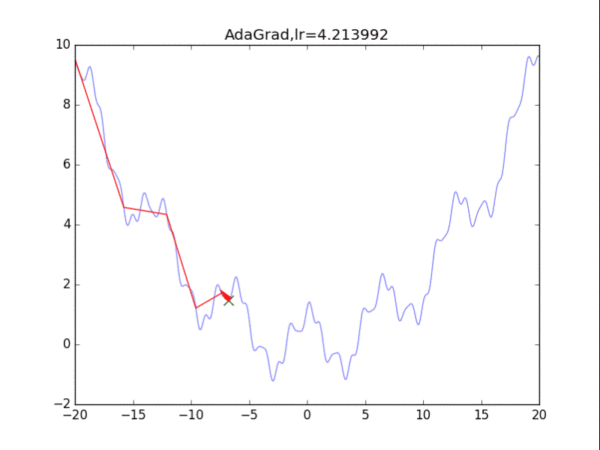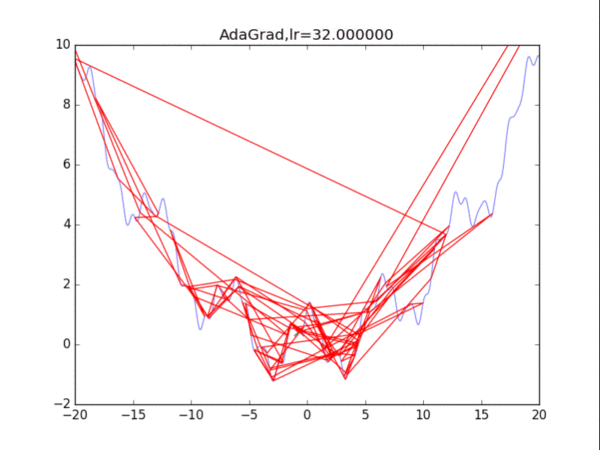
给出学习率lr，delta=1e-7累计梯度r=0，初始xwhile True：      g = df/dx      r  = r + g*g      x = x - lr / (delta+ sqrt(r)) * g

效果并不是很好......

算法4：RMSProp

AdaGrad算法在前期可能会有很大的梯度，自始至终都保留了下来，这会使得后期的学习率过小。RMSProp在这个基础之上，加入了平方梯度的衰减项，只能记录最近一段时间的梯度，在找到碗状区域时能够快速收敛。

算法描述：

给出学习率lr，delta=1e-6，衰减速率p累计梯度r=0，初始xwhile True：      g = df/dx      r  = p*r + （1-p）*g*g      x = x - lr / (delta+ sqrt(r)) * g

RMSProp,p=0.99

RMSProp,p=0.9

RMSProp,p=0.8

衰减速率情况复杂，建议自行调参.......

算法5：Adam算法

Adam算法和之前类似，也是自适应减少学习率的算法，不同的是它更新了一阶矩和二阶矩，用一阶矩有点像有动量的梯度下降，而用二阶矩来降低学习率。

此外还使用了类似于s = s / (1-p1^t)这样的公式，这样的公式在t较为小的时候会成倍增加s，从而让梯度更大，参数跑的更快，迅速接近期望点。而后续t比较大的时候，s = s / (1-p1^t)基本等效于s=s，没什么用。

算法如下：

给出学习率lr，delta=1e-8，衰减速率p1=0.9，p2=0.999 累计梯度r=0，初始x ,一阶矩s=0，二阶矩r=0时间t = 0while True：    t += 1    g = df/dx     s = p1*s + (1-p1) *g    r = p2*r +（1-p2）*g*g
    s = s / (1-p1^t)    r = r / (1-p2^t)
    x = x - lr / (delta+ sqrt(r)) * s

Adam算法，鬼一样的表现

是的，你没有看错，这玩意压根不收敛......表现极差。

在算法中仔细研究后才发现，是在t很小的前几步的时候，p2=0.999太大了，导致r = r / (1-p2^t) 中，1-p2^t接近0，r迅速爆炸，百步之内到了inf。后来修改p2=0.9后效果就好得多了。

Adam算法，神级表现

最后还是Adam效果最好了 ：)，尽管学习率还是需要相当的调参。

算法6：牛顿法

牛顿法是二阶近似方法的一种，其原理类似于将某函数展开到二次方（二次型）项：

如果幸运的话，这个展开式是一个开口向上的曲面，一步就走到这个曲面的最低点：

初始x while True：        g = df(x)  # 一阶导数        gg = ddf(x)   # 二阶导数        x = x - g/gg   # 走到曲面的最低点

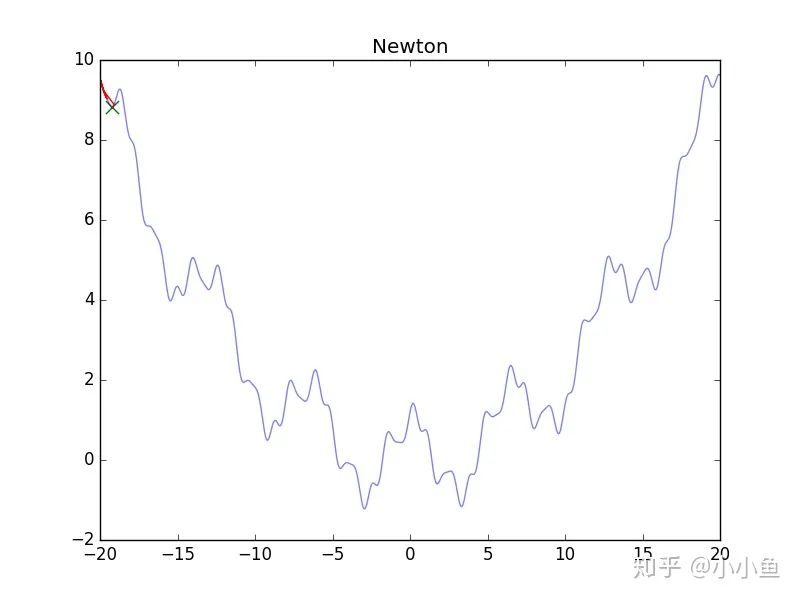可怜的牛顿法,静态图

图片如上，看了真可怜........其实牛顿法要求的是H矩阵正定（一维情况下是二阶导数大于零），在多维中，这样的情况难以满足，大量出现的极小值，悬崖，鞍点都会造成影响，导致无法顺利进行下去，为了更好地进行牛顿法，我们需要正则化它。

算法7：牛顿法+正则化

牛顿法加上正则化可以避免卡在极小值处，其方法也很简单：更新公式改成如下即可。

一维的算法如下：

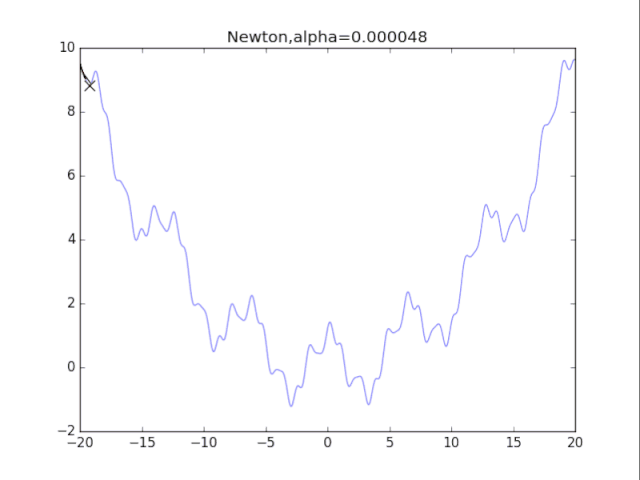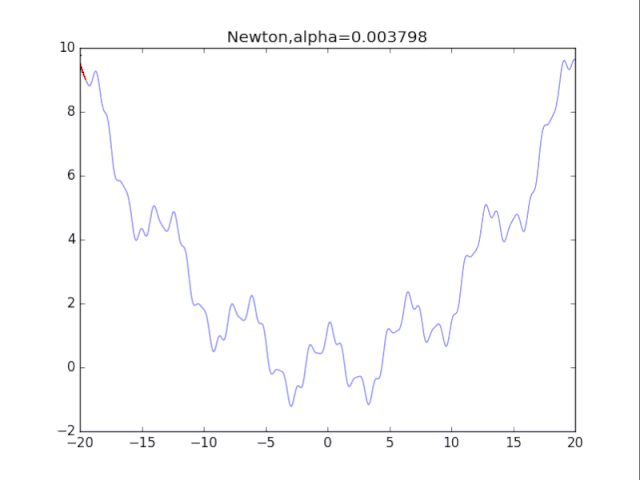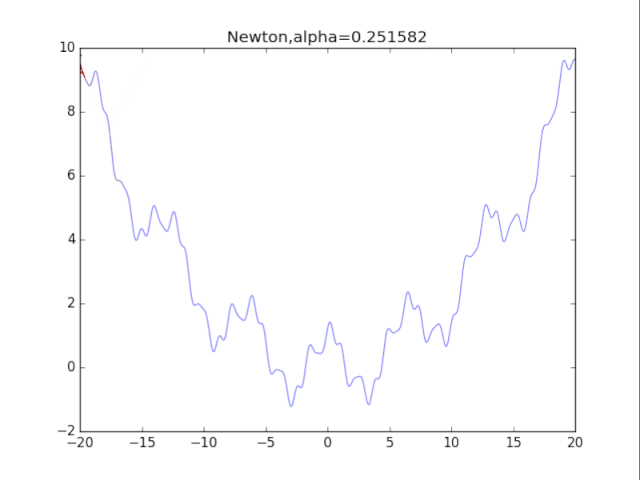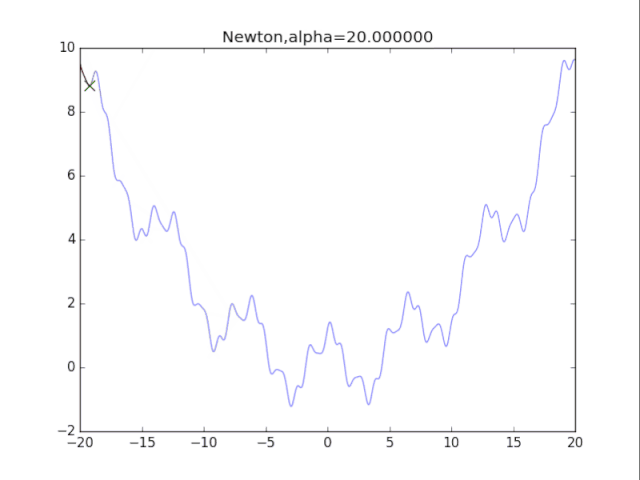
初始x  ，正则化强度alphawhile True：       g = df(x)  # 一阶导数                gg = ddf(x)   # 二阶导数                x = x - g/（gg+alpha）   # 走到曲面的最低点

效果图：

牛顿法+正则化

看了真可怜.........二次方法真心在非凸情况很糟糕。此外算法涉及H矩阵的逆，这需要O（n^3）的计算量，非深度学习可用。

   参考文献

[1]Ian Goodfellow，深度学习Deep Learning，人民邮电出版社,170-190

  代码

#coding:utf-8from __future__ import print_functionimport numpy as npimport matplotlib.pyplot as plt
def f(x):    return (0.15*x)**2 + np.cos(x) + np.sin(3*x)/3 + np.cos(5*x)/5 + np.sin(7*x)/7
def df(x):    return (9/200)*x - np.sin(x) -np.sin(5*x) + np.cos(3*x) + np.cos(7*x)
points_x = np.linspace(-20, 20, 1000)points_y = f(points_x)

# 纯粹的梯度下降法,GDfor i in range(10):    # 绘制原来的函数    plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")    # 算法开始    lr = pow(2,-i)*16    x = -20.0    GD_x, GD_y = [], []    for it in range(1000):        GD_x.append(x), GD_y.append(f(x))        dx = df(x)        x = x - lr * dx
    plt.xlim(-20, 20)    plt.ylim(-2, 10)    plt.plot(GD_x, GD_y, c="r", linestyle="-")    plt.title("Gradient descent,lr=%f"%(lr))    plt.savefig("Gradient descent,lr=%f"%(lr) + ".png")    plt.clf()

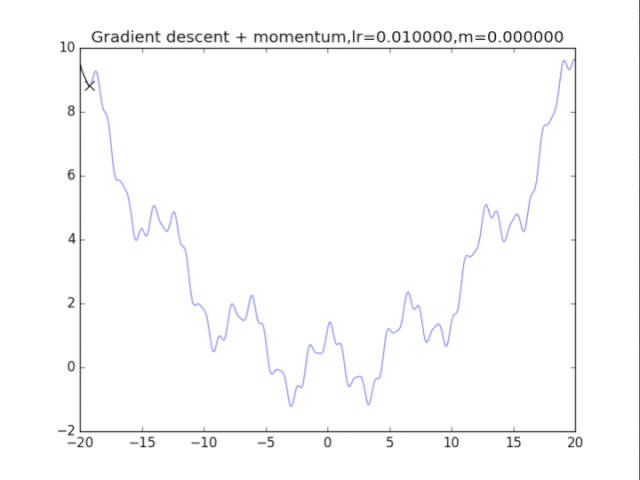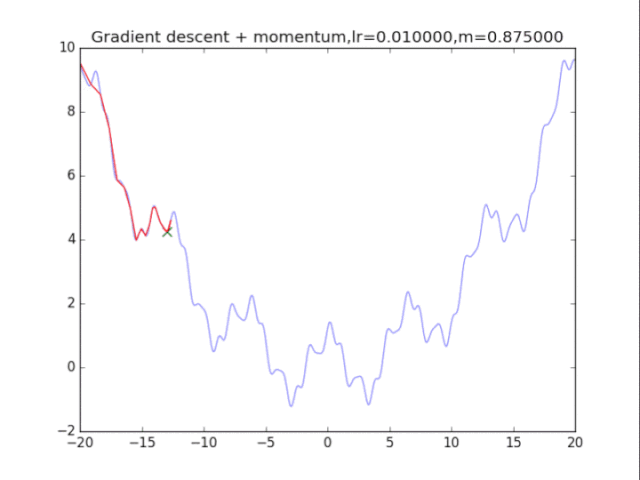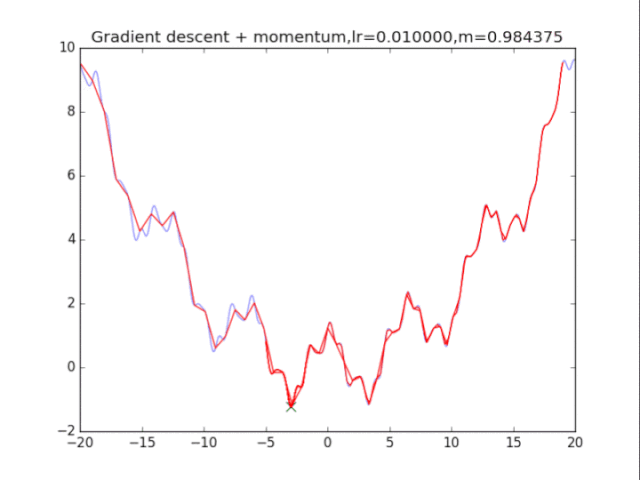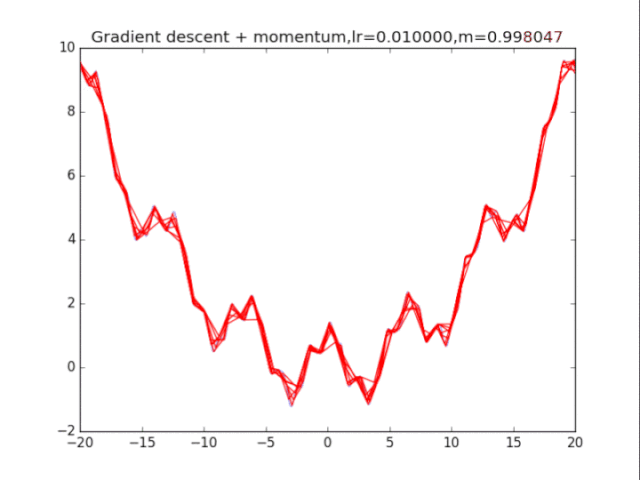
# 动量 + 梯度下降法for i in range(10):    # 绘制原来的函数    plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")    # 算法开始    lr = 0.002    m = 1 - pow(0.5,i)    x = -20    v = 1.0    GDM_x, GDM_y = [], []    for it in range(1000):        GDM_x.append(x), GDM_y.append(f(x))        v = m * v - lr * df(x)        x = x + v
    plt.xlim(-20, 20)    plt.ylim(-2, 10)    plt.plot(GDM_x, GDM_y, c="r", linestyle="-")    plt.scatter(GDM_x[-1],GDM_y[-1],90,marker = "x",color="g")    plt.title("Gradient descent + momentum,lr=%f,m=%f"%(lr,m))    plt.savefig("Gradient descent + momentum,lr=%f,m=%f"%(lr,m) + ".png")    plt.clf()

# AdaGradfor i in range(15):    # 绘制原来的函数    plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")    # 算法开始    lr = pow(1.5,-i)*32    delta = 1e-7    x = -20    r = 0    AdaGrad_x, AdaGrad_y = [], []    for it in range(1000):        AdaGrad_x.append(x), AdaGrad_y.append(f(x))        g = df(x)        r = r + g*g # 积累平方梯度        x = x - lr /(delta + np.sqrt(r)) * g
    plt.xlim(-20, 20)    plt.ylim(-2, 10)    plt.plot(AdaGrad_x, AdaGrad_y, c="r", linestyle="-")    plt.scatter(AdaGrad_x[-1],AdaGrad_y[-1],90,marker = "x",color="g")    plt.title("AdaGrad,lr=%f"%(lr))    plt.savefig("AdaGrad,lr=%f"%(lr) + ".png")    plt.clf()

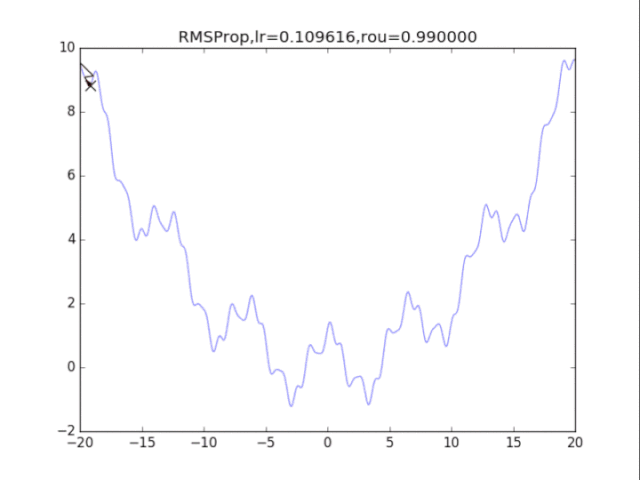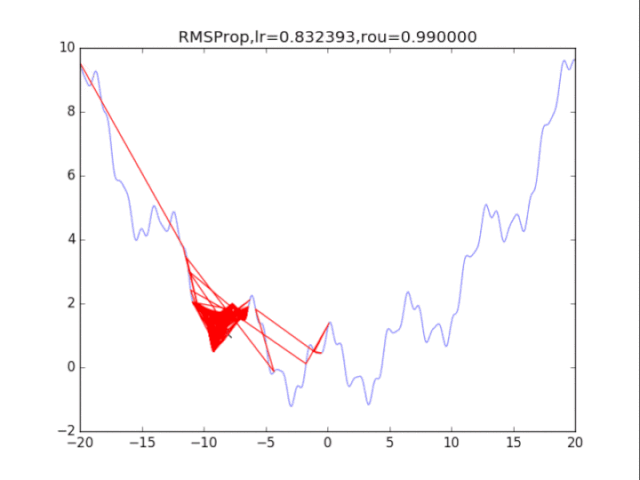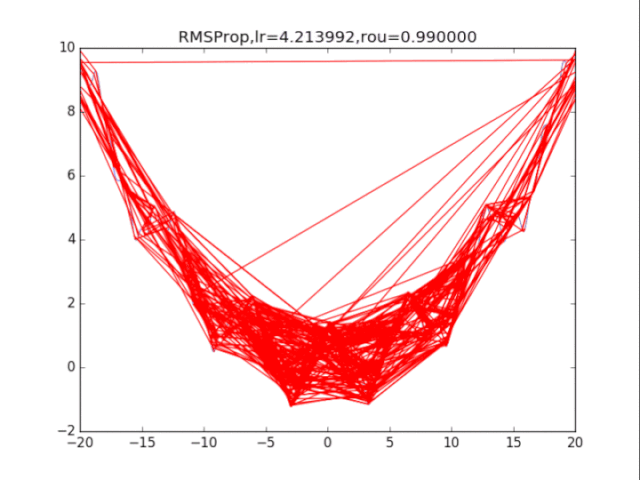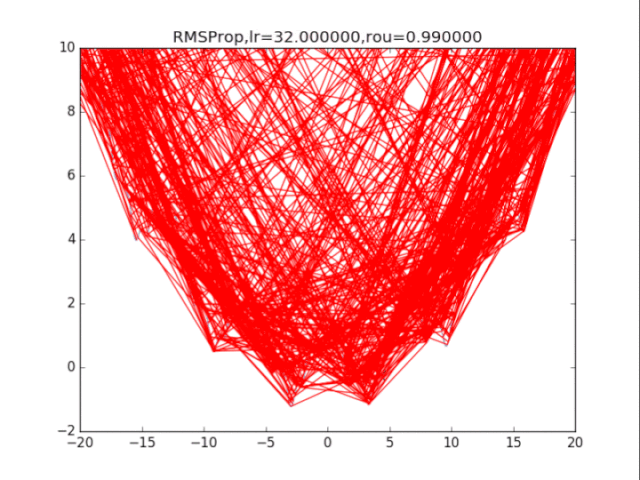
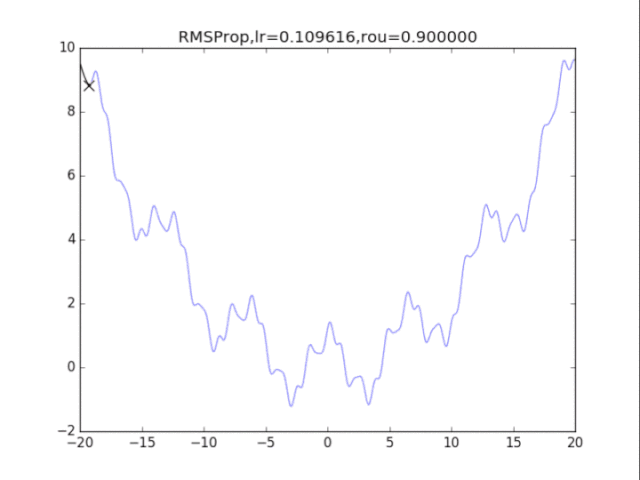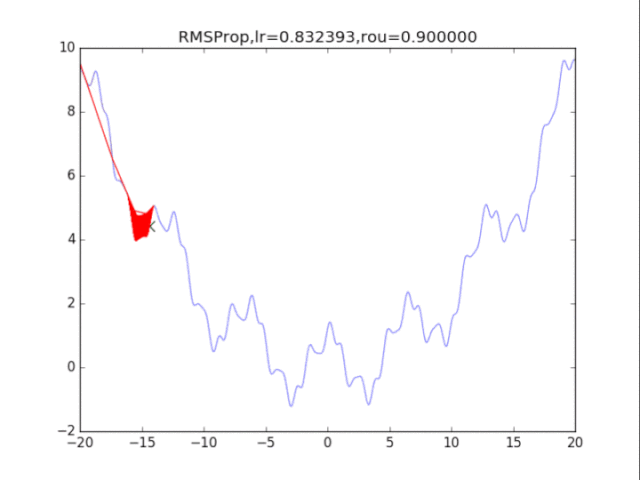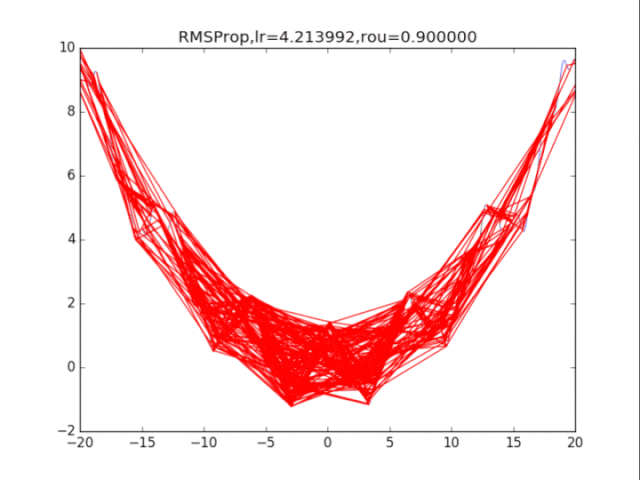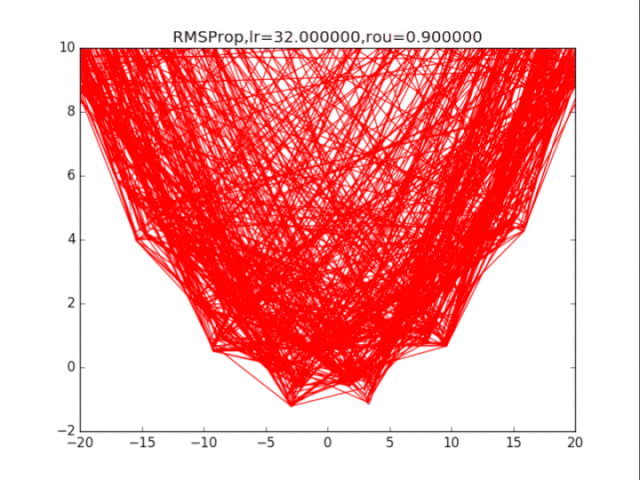
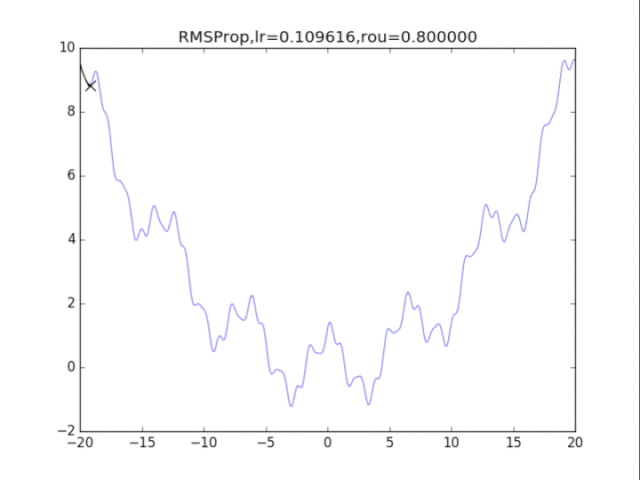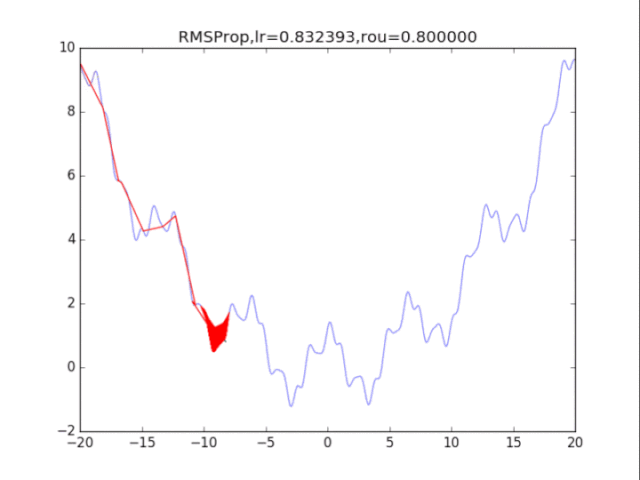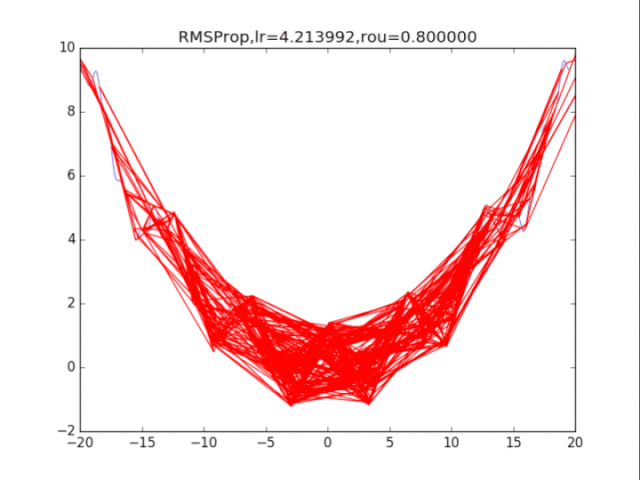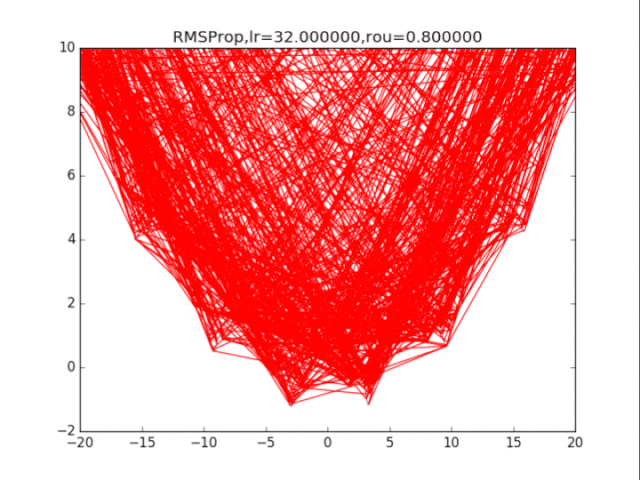
# RMSPropfor i in range(15):    # 绘制原来的函数    plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")    # 算法开始    lr = pow(1.5,-i)*32    delta = 1e-6    rou = 0.8    x = -20    r = 0    RMSProp_x, RMSProp_y = [], []    for it in range(1000):        RMSProp_x.append(x), RMSProp_y.append(f(x))        g = df(x)        r = rou * r + (1-rou)*g*g # 积累平方梯度        x = x - lr /(delta + np.sqrt(r)) * g
    plt.xlim(-20, 20)    plt.ylim(-2, 10)    plt.plot(RMSProp_x, RMSProp_y, c="r", linestyle="-")    plt.scatter(RMSProp_x[-1],RMSProp_y[-1],90,marker = "x",color="g")    plt.title("RMSProp,lr=%f,rou=%f"%(lr,rou))    plt.savefig("RMSProp,lr=%f,rou=%f"%(lr,rou) + ".png")    plt.clf()
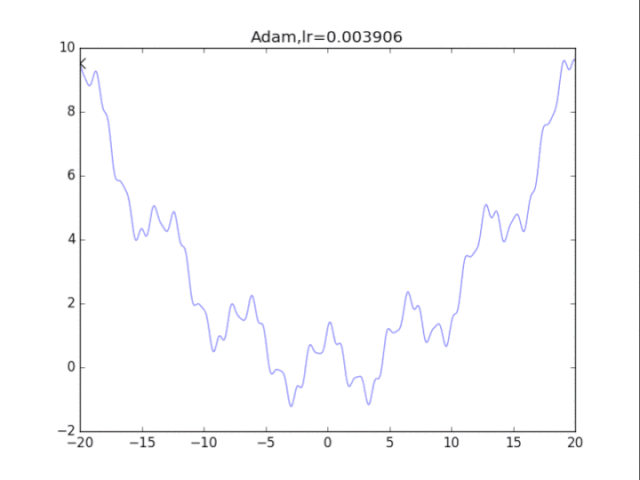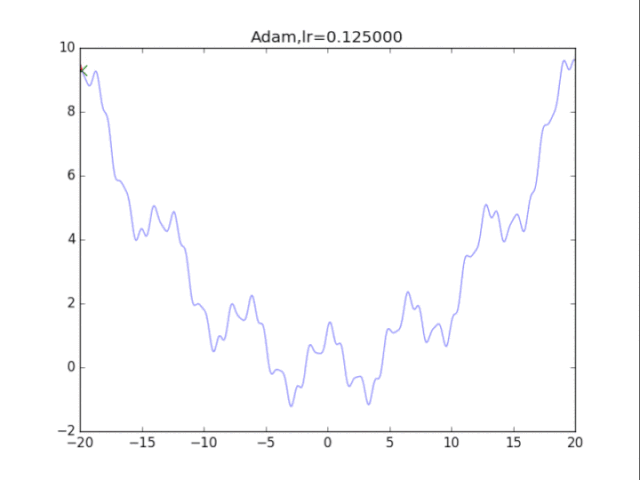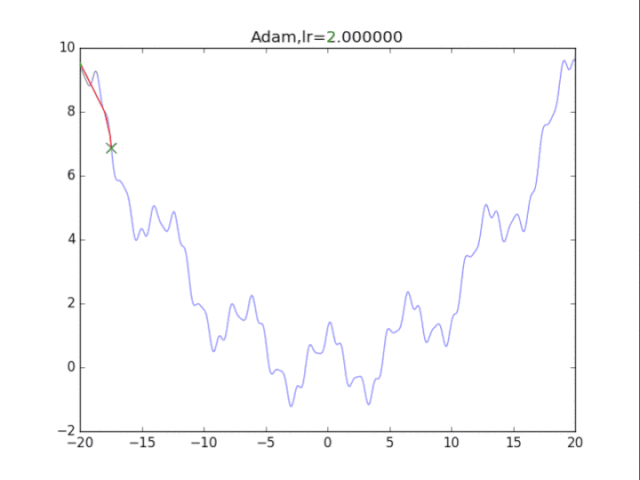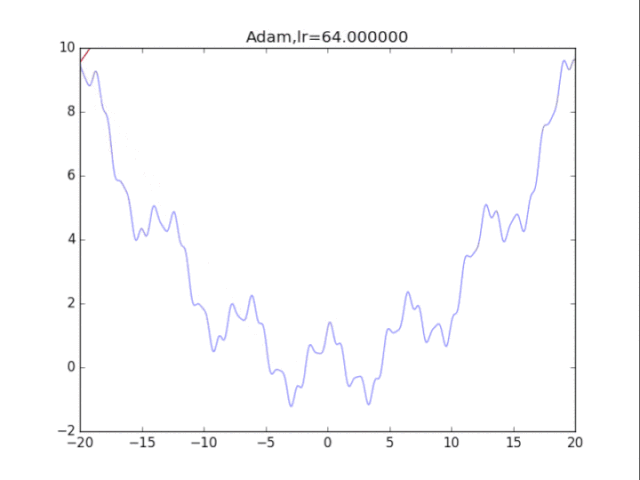
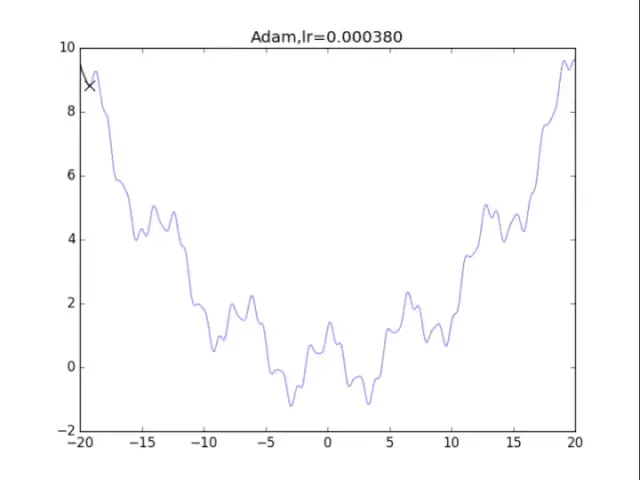
# Adamfor i in range(48):    # 绘制原来的函数    plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")    # 算法开始    lr = pow(1.2,-i)*2    rou1,rou2 = 0.9,0.9  # 原来的算法中rou2=0.999，但是效果很差    delta = 1e-8    x = -20    s,r = 0,0    t = 0    Adam_x, Adam_y = [], []    for it in range(1000):        Adam_x.append(x), Adam_y.append(f(x))        t += 1        g = df(x)        s = rou1 * s + (1 - rou1)*g        r = rou2 * r + (1 - rou2)*g*g # 积累平方梯度        s = s/(1-pow(rou1,t))        r = r/(1-pow(rou2,t))        x = x - lr /(delta + np.sqrt(r)) * s
    plt.xlim(-20, 20)    plt.ylim(-2, 10)    plt.plot(Adam_x, Adam_y, c="r", linestyle="-")    plt.scatter(Adam_x[-1],Adam_y[-1],90,marker = "x",color="g")    plt.title("Adam,lr=%f"%(lr))    plt.savefig("Adam,lr=%f"%(lr) + ".png")    plt.clf()
# 牛顿法for i in range(72):    # 绘制原来的函数    plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-")    # 算法开始    alpha= pow(1.2,-i)*20    x = -20.0    Newton_x, Newton_y = [], []    for it in range(1000):        Newton_x.append(x), Newton_y.append(f(x))        g = df(x)        gg = ddf(x)        x = x - g/(gg+alpha)
    plt.xlim(-20, 20)    plt.ylim(-2, 10)    plt.plot(Newton_x, Newton_y, c="r", linestyle="-")    plt.scatter(Newton_x[-1],Newton_y[-1],90,marker = "x",color="g")    plt.title("Newton,alpha=%f"%(alpha))    plt.savefig("Newton,alpha=%f"%(alpha) + ".png")    plt.clf()

说个正事哈


由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：
（1）点击页面最上方“深度学习自然语言处理”，进入公众号主页。
（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。
感谢支持，比心。


投稿或交流学习，备注：昵称-学校（公司）-方向，进入DL&NLP交流群。
方向有很多：机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。
记得备注呦

推荐两个专辑给大家：
专辑 | 李宏毅人类语言处理2020笔记
专辑 | NLP论文解读