KDD'20 Best Paper | 推荐系统中采样测试的误区
点击上方蓝字关注我们!
Walid Krichene and Steffen Rendle. 2020. On Sampled Metrics for Item Recommendation. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD '20). DOI:https://doi.org/10.1145/3394486.340322
引言




Evaluation Metrics



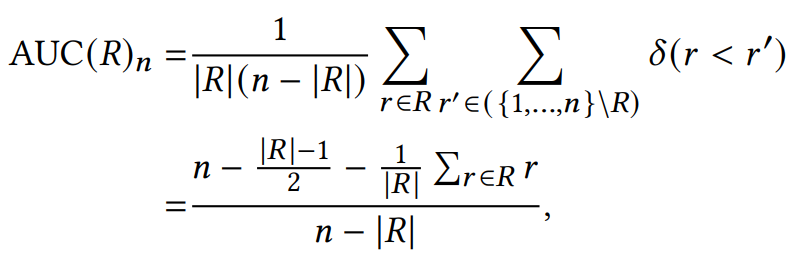
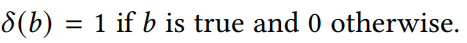
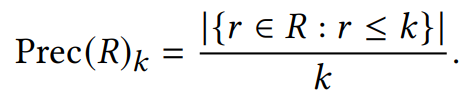
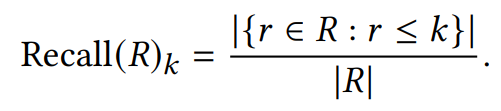
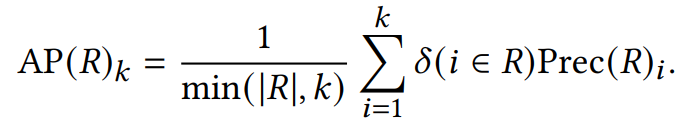
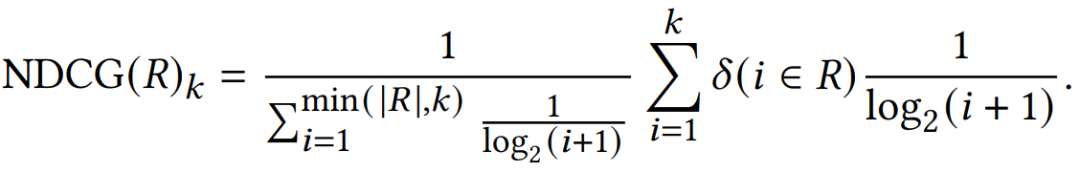
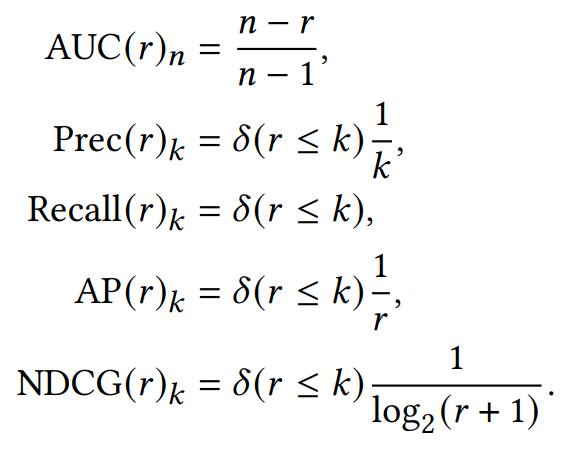
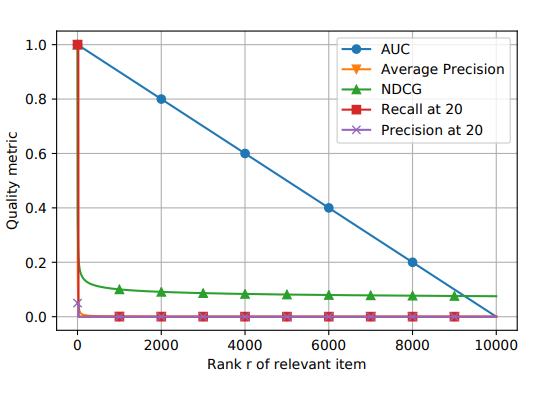
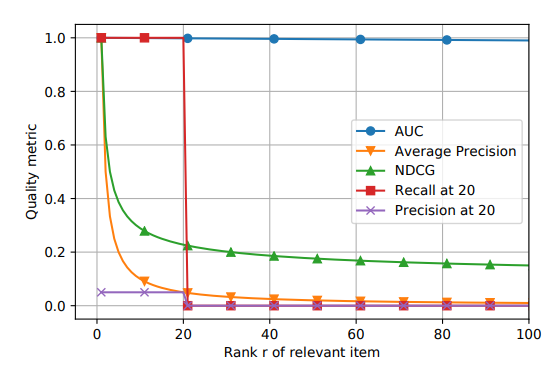

这个三个系统的不同点在于:
-
A系统对相关items排序基本上都不高不低,但是因为item数量很多(10K)所以AUC表现很好,而其他三个指标,尤其是recall,都是比较低的值。 -
B系统对其中两个relevant items排序比A系统要好,排到了40,而其他的都很差,所以整体的AUC表现很差。 -
C系统只对一个相关item排序很好,排到了rank 2,其他的表现都很差,所以此时AUC也是较差,但是另外三个指标都很好。所以可以看出其他三个指标是对靠前的相关item更加敏感,会给出更高的score,这也符合推荐系统的衡量标准——越靠前越好。
Sampled Metrics (采样评估)



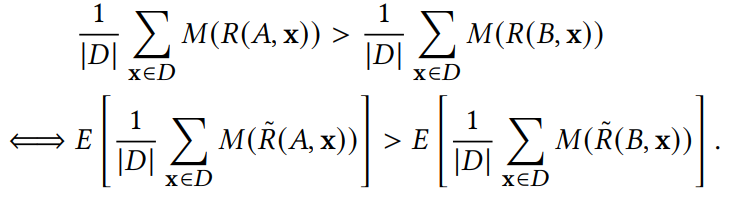
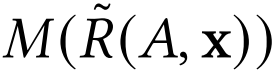 是指在sampled metric M下, A推荐系统的ranking。
是指在sampled metric M下, A推荐系统的ranking。

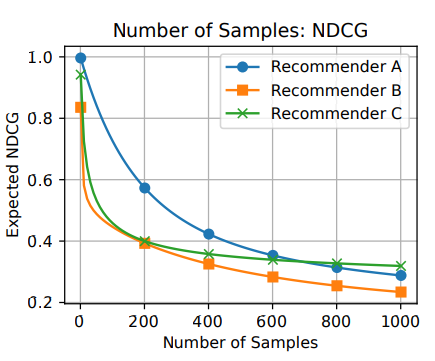
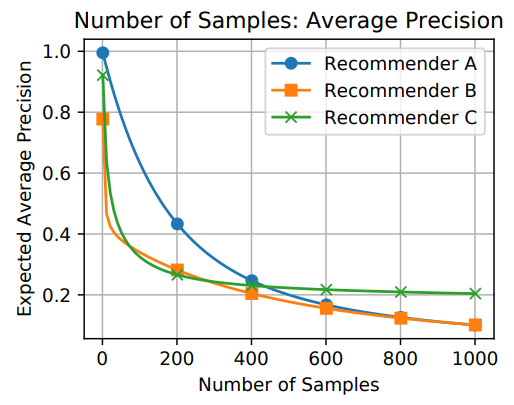
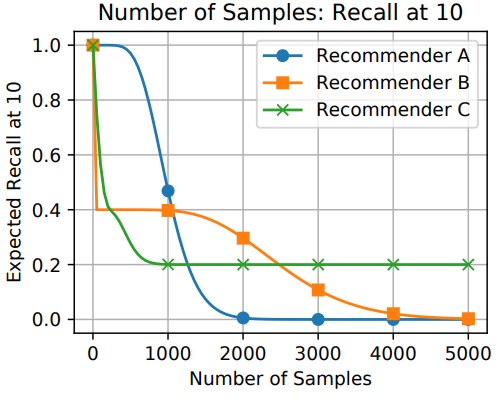
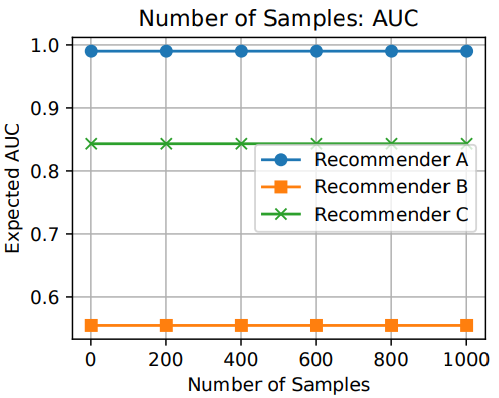
采样评估的数学期望



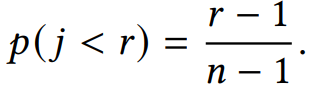
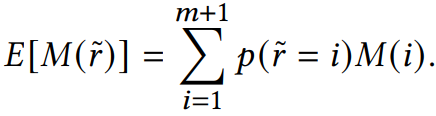
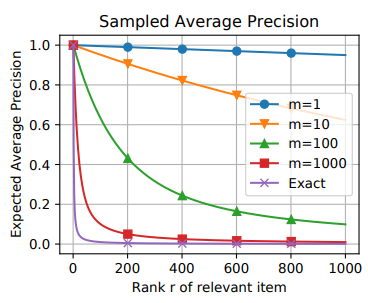
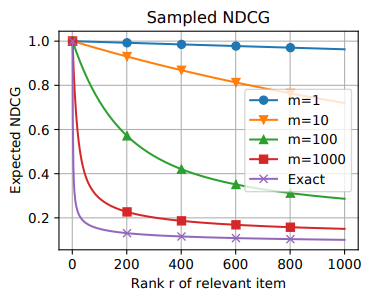
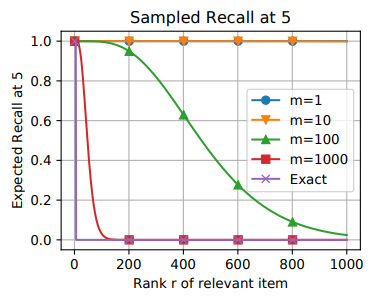
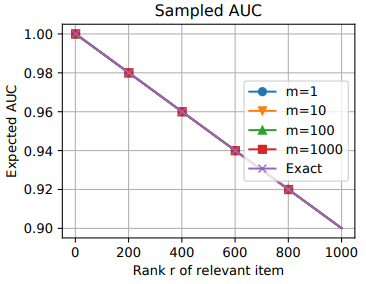
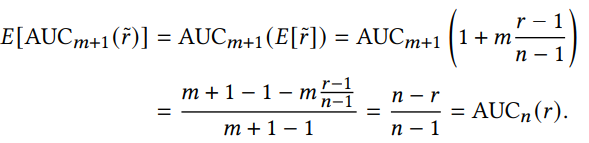
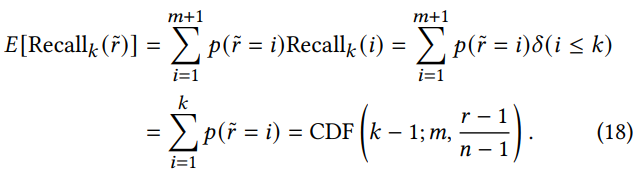
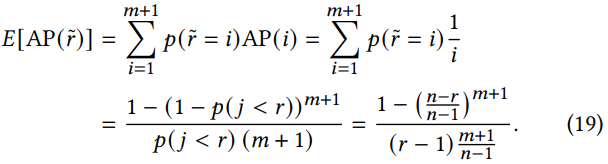
采样评估的校正



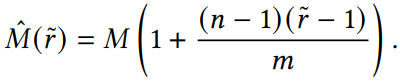
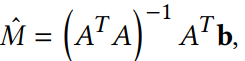
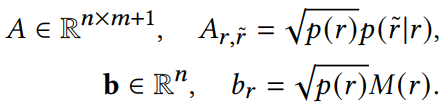
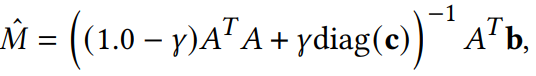
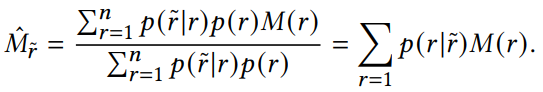
实验



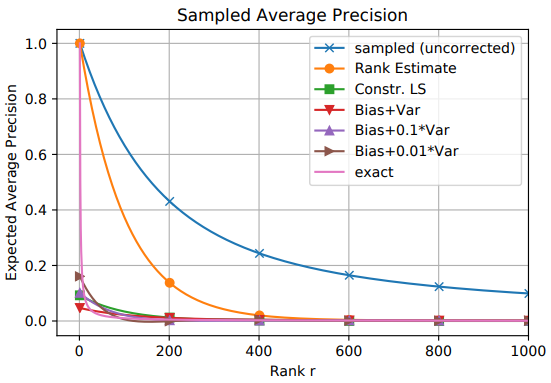
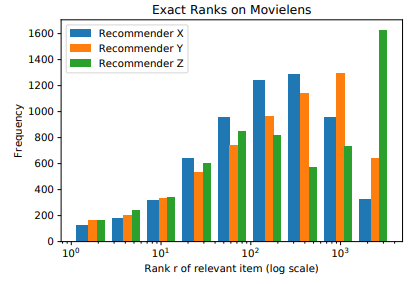
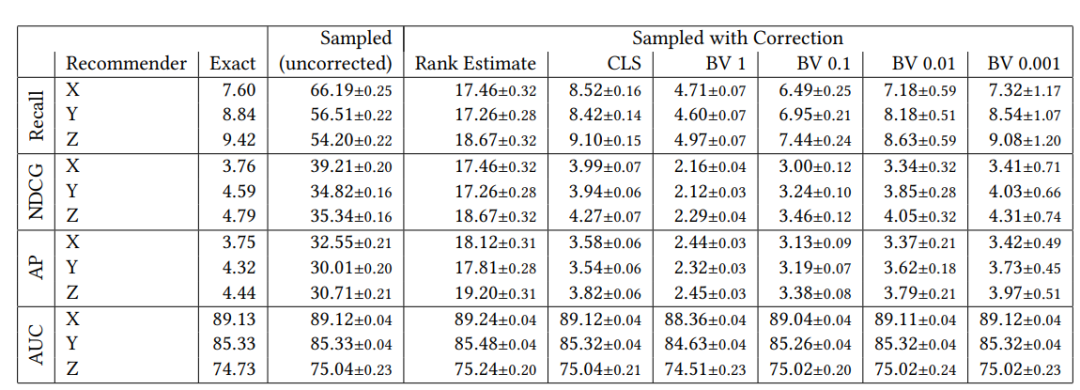
结论



-
MLP or 点积 | 如何建模推荐系统中用户商品交互?
-
深入理解推荐系统:召回 -
KDD’19 | 预测用户和商品的动态嵌入趋势 -
SIGIR‘19 | 图神经网络协同过滤算法-Neural Graph Collaborative Filtering -
WSDM'20 | 如何构建推荐系统中的商品知识图谱
登录查看更多
相关内容
推荐系统,是指根据用户的习惯、偏好或兴趣,从不断到来的大规模信息中识别满足用户兴趣的信息的过程。推荐推荐任务中的信息往往称为物品(Item)。根据具体应用背景的不同,这些物品可以是新闻、电影、音乐、广告、商品等各种对象。推荐系统利用电子商务网站向客户提供商品信息和建议,帮助用户决定应该购买什么产品,模拟销售人员帮助客户完成购买过程。个性化推荐是根据用户的兴趣特点和购买行为,向用户推荐用户感兴趣的信息和商品。随着电子商务规模的不断扩大,商品个数和种类快速增长,顾客需要花费大量的时间才能找到自己想买的商品。这种浏览大量无关的信息和产品过程无疑会使淹没在信息过载问题中的消费者不断流失。为了解决这些问题,个性化推荐系统应运而生。个性化推荐系统是建立在海量数据挖掘基础上的一种高级商务智能平台,以帮助电子商务网站为其顾客购物提供完全个性化的决策支持和信息服务。
Arxiv
0+阅读 · 2020年12月2日
Arxiv
0+阅读 · 2020年11月27日




