【NeurIPS 2021】流形上的注意力机制：规范等变的Transformer

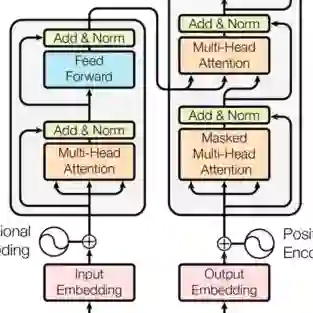
近几年来，Transformer模型在学界和工业界正受到越来越广泛的关注，它的一大特点就是可以根据附近上下文信息的内容赋予不同的注意力权重。Transformer的优越性也促使研究者们希望将其应用到其它的研究领域上，例如计算机视觉或者图网络学习等。

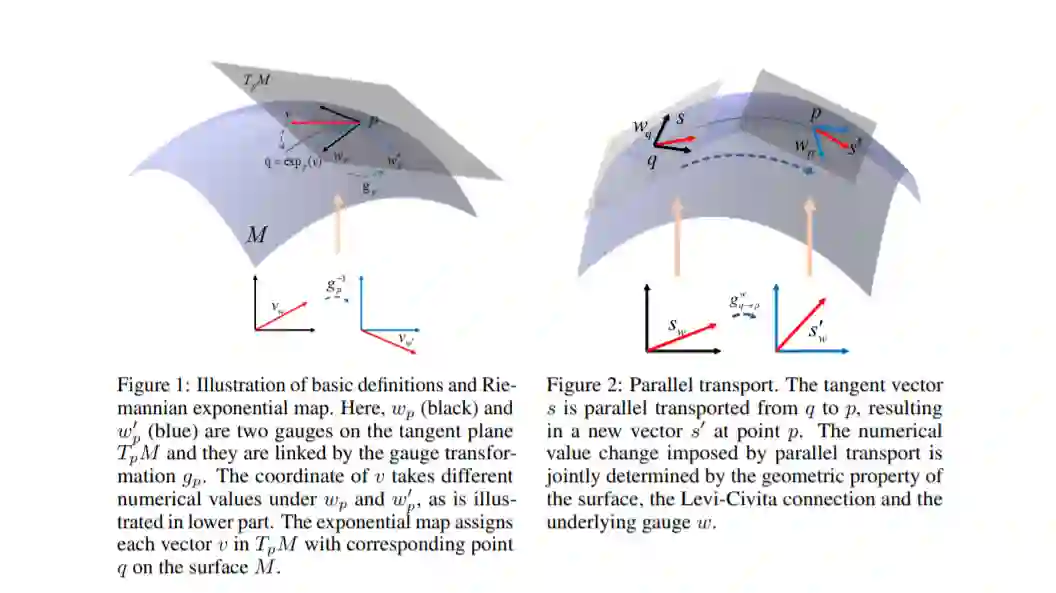
现在我们希望将Transformer结构应用到流形（Manifold）上。先回忆一种简单的情况：当Transformer应用到2D图片上时，它会以一个像素为中心点，综合考虑附近邻域中每一个像素的内容并进行加权信息聚合。在这个过程中，附近邻域中的每一个像素相对中心像素都有一个明确而清晰的位置，并且这个相对位置有一个统一的参数化模式。然而，对于流形这种不规则的数据结构，在Transformer进行信息聚合时，邻域点的相对位置信息存在无数种参数化模式，这种不唯一性会影响计算机进行数据处理和模式识别的结果。

https://openreview.net/pdf?id=fyL9HD-kImm

本文主要贡献如下：

• 我们首次提出了规范等变的注意力机制模型（Gauge Equivariant Transformer，简称为GET）。我们从数学上证明了GET对于旋转角度为 （N为正整数）的规范改变上是完全等变的，并且对其它的旋转角度给出了等变误差的上界。
• 我们精心设计了一种与全局坐标系无关的模型输入。这种输入与规范等变性相结合可以实现三维空间内物体的旋转不变性。
• 我们提出了一种新的平行移动方法，即把循环群的正规表示扩展到了2D空间任意旋转群的表示。相比传统的截断或插值方法，我们的方法可以保留更多的流形几何信息。
• 我们使用泰勒级数来求解等变的限制条件，从而在邻域中有更好的近似效果。
• 我们通过实验证明了模型的有效性。在SHREC数据集上，GET比最好的baseline模型HSN有3.1%的准确率提升；在Human Body Segmentation数据集上，GET比最好的baseline模型MeshCNN有0.3%的准确率提升。

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“GET” 就可以获取《【NeurIPS 2021】流形上的注意力机制：规范等变的Transformer》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源