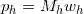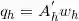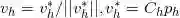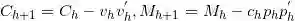数据分析师应该知道的16种回归技术:偏最小二乘回归
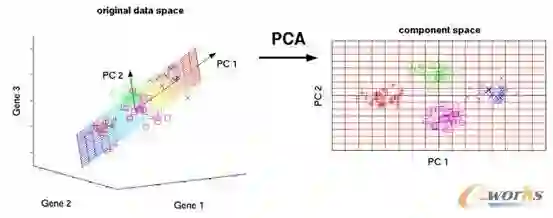
对于线性回归模型,当预测变量具有多重共线性,或者预测变量比观测值多。若依然采用普通的最小二乘(OLS)算法进行参数估计,往往出现估计偏差大,模型不能反映变量间的真实关系。对于这个问题,我们可以使用主成份回归(PCR),由于PC间相互独立,这样的话就不会有多重共线性问题。然而,PCR存在三点不足:(a)PC可能与因变量Y有关;(b)可能前p-1个pc与因变量都无关,最后一个pc解释了因变量的所有变异;(c)PCA只适用于一维因变量。今天介绍的偏最小二乘回归(PLSR)基本上就是对这些不足的弥补。
PLSR依赖于自变量X和因变量Y的主成份,核心思想是首先算出X和Y的主成份得分阵,然后对得分阵进行回归。
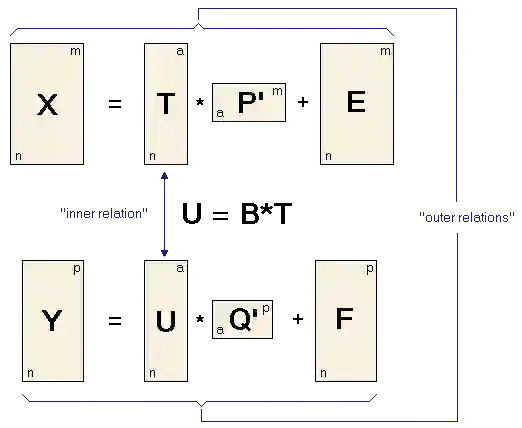
如上图所示,X被分解成得分阵T和载荷阵P'的乘积再加上误差阵E。Y被分解成了得分阵U和载荷阵Q'的乘积再加上误差项F,称这两个等式为回归模型的外部关系。PLS算法的目标是最小化误差F的范数同时通过内部关系U=BT保持X与Y之间的相关关系。
常用来进行PLSR的算法有两种:NIPALS和SIMPLS。下面给出两种方法的计算过程:
NIPALS
设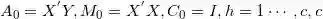
计算
的特征向量
设
,其中
,
设
,其中
,
,
设
,其中
SIMPLS
设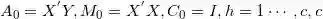
计算
的特征向量
设
,其中
,
,
设
,其中
设
,其中
然后求的系数估计值为:
就计算效率而言后者要优于前者。因此在进行PLSR时,常选用SIMPLS算法。R软件pls包中的plsr可以实现此方法。最后一个问题是确定PLS模型中主成份的个数,可采用交叉验证的方法求解不同个数主成份下模型的预测均方根误差(RMSEP)。
案例:
我们采用的数据集是oliveoil,该数据集从颜色(黄、绿、棕)、光泽、透明度、糖汁6个物理属性描述16种橄榄油样本的5种化学属性,其中前5种来自希腊,中间5种来自意大利和剩余样本来自西班牙。
library(pls)
X <- oliveoil$sensory
Y <- oliveoil$chemical
pls1 <- plsr(X ~ Y,validation = "LOO")
plot(RMSEP(pls1), legendpos = "topright")
上图表明,选用两个主成份,橄榄油各物理指标的PRMSE达到相对较小的值。最终得到不同物理指标下回归系数如下:
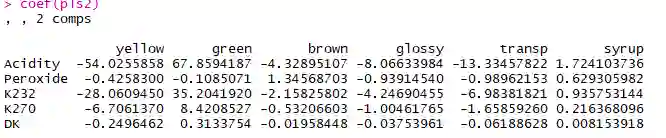
pls2 <- plsr(X ~ Y ,ncomp = 2,validation = "LOO")
coef(pls2)
推荐阅读

长按二维码关注“数萃大数据”
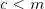
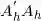 的特征向量
的特征向量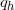
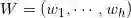 ,其中
,其中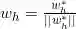 ,
,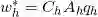
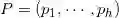 ,其中
,其中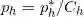 ,
,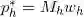 ,
,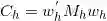
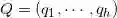 ,其中
,其中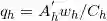
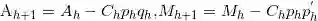
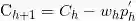
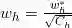 ,
,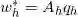 ,
,