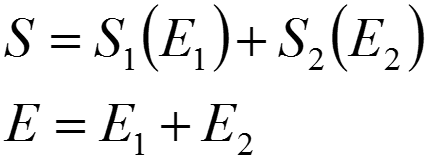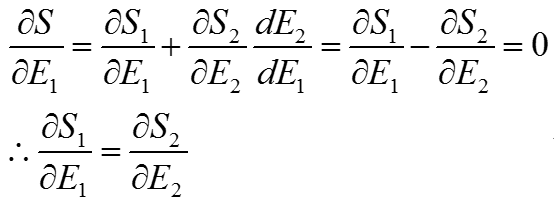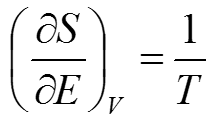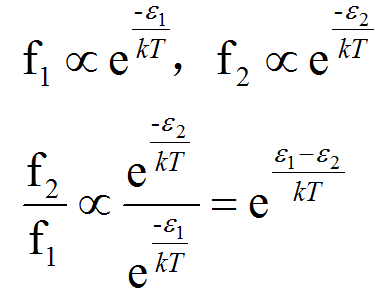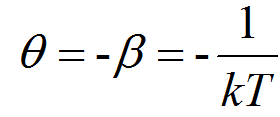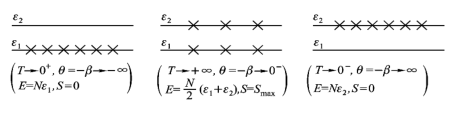比绝对零度还低？比无穷温度还高？神奇的负温度究竟是什么鬼？

会员服务 ·

比绝对零度还低？比无穷温度还高？神奇的负温度究竟是什么鬼？ | No.105

2018 年 5 月 18 日 中科院物理所 Frions

上一期在后台收到很多小伙伴们对负温度的提问，

那么这期我们的答题小哥就加班加点赶出了“今天的什么是负温度？”。

负温度不是指极低的温度，相反，

它描述的是一种温度达到正无穷以后的温度！！

这究竟是人性的扭曲还是道德的沦丧？

友情提示：这个问题再最后一个，没耐心的小伙伴可以直接拉到最后。

搭配BGM食用更佳 ╭(●｀∀´●)╯（点击音频图标即可食用）

怎么样！才能！减肥！

by 焦糖爆米花

看到这个问题，我第一反应是这个问题的答案应该非常非常多吧？

于是我上了国内某搜索网站，输入了这个问题。果然不出我所料，首先看到的是各种广告。而往下翻则能看到各种干货、经验贴。

所以粉丝问这个问题，自然是希望得到物理式的答案。

首先告诉你一点——你选对地方了！

在分析这个物理问题之前，让我们先定义一个名词。

表观体重：实验上通过仪器所测到的体重，得到的数据是数字，从几十到几百分布，单位为KG。

我们先来聊一下狭义的减肥，即改变表观体重。

你决定要减肥了，那么此时你的表观体重就是初始值，你当然会有一个目标体重，虽然这个目标体重可能于你而言像绝对零度一样不能通过有限的手续达到……

从数学上看，就是给定了初末端点，求连接两端点之间的曲线函数，要求满足时间最短或是最“轻松”，这是典型的泛函求极值问题，可以用变分法来解。

找出各种变量后构建出适合的拉氏量，然后求解欧拉-拉格朗日方程，理论上可以解出一个减肥的最佳策略。

Emmm，让我们绕开这个数学问题，来一点简单粗暴的物理减肥法。

有个公式我们都很熟悉，E=mc²

如果站在质量亏损的角度来看，那么想减小表观体重需要释放大量的能量，所以我们减肥并不是通过这条途径。

我们需要吃饭一方面是为了获取能量，另一方面则是从食物里获取一些人体必须的物质参与人体的合成与代谢，比如氨基酸、维生素、无机盐等。从能量的角度来分析，如果摄入的能量比消耗的多，那么表观体重对于时间的导数便会取正值，所以如果长期吃的多却消耗的少就会长肉。

因此想要减肥得从两方面入手，一是减少能量摄入，二是增大能量消耗。

增大能量消耗所要面对的障碍无非就是累和懒，但减少能量摄入则是要抵制成千上万的美食，所以减肥的重心应该放在增大能量消耗上。可以做一些运动，比如跑步、跳绳、游泳等。另一方面，大脑在进行高强度思考时对能量的消耗也很大，比如人即便坐着不动，但是在那做数学题，则饿的会很快。

接下来我们来聊一聊广义的减肥。

在广义减肥的理论框架里，表观体重只是一个参照，远不及在侠义减肥论中重要。

在进一步讨论之前，我们需要再定义两个名词。

主观体重：与质量m无关，是人对自己体重的一个认识。比如在A看来很瘦的B却经常吐槽自己又胖了怎么怎么的，而在A、B看来很胖的C则认为自己还是挺苗条的。

客观体重：与质量m无关，是别人对你体重的一个认识。比如A对B说：你看你都胖了，所以这些肉你就都让给我吃吧。

只有当一个人在主观上觉得自己胖了的时候才会决定去减少自己的表观体重，而客观体重的影响最终其实也是在影响主观体重。当一个人主观上觉得自己的体重可以了，自然就不会想去减肥了。所以，真正要改变的其实是主观体重！

也就是说，我们真正追求的，其实并不是体重秤上的读数，而是自己以及周边的人都认为自己苗条、性感。所以可以通过穿衣来凸显自己的苗条，扬长避短。

也许你会说，那上秤不就暴露了吗？

很简单，你只需说三个字——你先上！

By Patwf

气球为什么飞不到外太空去？

by 匿名君

气球里边的气体不仅要抵抗大气压，还要抵抗气球的弹力，随着高度的升高，大气中的气体逐渐变的稀薄起来，气压会降低，那么在地面上达到的平衡现在就平衡不了了，为了平衡气球就必须要膨胀以降低内部的气压，而膨胀到一定程度就爆炸了。

Emmmm如果气球的材质能逆天呢？

这个气球一路披荆斩棘，穿过了对流层、平流层、中间层，不惧电离层的各种摧残、愈发变强的紫外线只等闲，散逸层千度的高温一笑而过……

在考虑这些之前，让我们思考一个问题——气球为什么能飞起来？

气球能够飞起来是因为里边的密度比外边的密度要小，因此相当于是受到了大气的浮力。随着高度的升高，大气的密度也会降低，但由于气球在膨胀，所以气球内部气体的密度也在减小，因此还是能受到浮力的。但散逸层的大气密度只有海平面处的一亿亿分之一，气球怕是膨胀不了一亿亿倍吧……

结果就是最终浮力会与重力平衡，气球悬浮在空中。

By Patwf

为什么坐车时总觉得远的东西在往前走，而近的东西在往后走（以行车方向为前）

by PEACE

如果你想看到一个物体在向后走，首先这个物体相对你的速度一定是要向后的。但是不论是远处的物体还是近处的物体都可以满足这个要求，为什么会给人不同的感觉？这是大脑的认知在作怪：对于近处的物体，即使物体稍微向后移动，物体相对人的方位角也会有明显的变化，人就能很明显的感受到物体在后退。但是对于远处的物体，即使物体移动较大的距离，物体相对于人的方位角依然没有明显变化，所以人就默认物体一直相对自己没有运动，又因为他自己在动，所以他会认为物体在跟着自己往前走。月亮跟着自己走以及高速公路上无法看清窗外近处的物体但是能看清远处的物体也是同样的道理。

By Nothing

3D眼镜如何让我们看到立体的图像?

by 在世开普勒

人的两眼间距约5公分，在看物体时，两只眼睛看到的角度并不完全相同，即存在两个视角。大脑可以根据视角的差别区分出景物的前后远近，进而产生强烈的立体感。

3D电影在拍摄时利用两台并列安置的电影摄影机，分别代表人的左、右眼，同步拍摄出两条略带水平视差的电影画面。放映时，将两条电影影片分别装入左、右放映机。当画面投放于电影银幕时，就会形成左、右“细微”的双重影像。特制的3D眼镜能将左、右“双影”分别传输给左右眼，由大脑产生三维立体的视觉效果，从而展现出一幅幅连贯的立体画面，让观众感受到景物扑面而来、“身临其境”的神奇幻觉。

By Nothing

请问空间站工作的宇航员受力为什么不平衡？

by 余静

为了简单起见，我们把讨论限制在飘在空中的宇航员身上。宇航员飘在太空中的时候只会受到到地球引力的影响（忽略其他天体和稀薄的气体的作用力），处于完全失重的状态。那么为什么宇航员没有掉下来呢？这是因为宇航员在绕地球做圆周（或椭圆）运动，这种运动本身就需要向心力的维持，地球引力刚好充当了这个向心力使得宇航员绕着地球运动而不会掉下来。

By Nothing

为什么使用显微镜观察时把低倍镜换成高倍镜，视野会变暗？

by 涵

显微镜有目镜、物镜，物镜对被观察物体成实像，而目镜的作用则是把物镜放大的实象（中间象）再放大，并把物象映入观察者的眼中用于人眼观察，它成的是虚像。

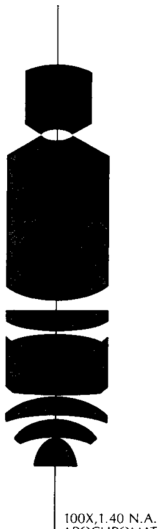
首先我们看一看物镜的外形。

（图片来自知乎，李雷）

我们可以看到放大倍数越大则进光口越小，因此进入物镜的光变少了。就好比你把一个纸卷成纸筒，透过它看手机屏幕，则纸筒的半径越小所能看到的手机屏幕大小就越小。而目镜是没有变化的，所以最终眼睛看到的图像大小没有变，亮度自然就变暗了。就好比在烙饼，保持饼的面积不变，如果你的面多那么烙的饼就厚，而面少则烙的饼就薄。

但是并不能说高倍镜的聚光能力不如低倍镜，恰恰相反，高倍镜的聚光能力更强！

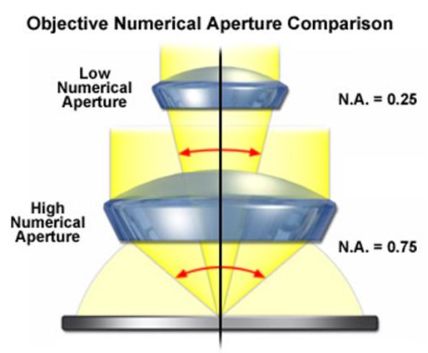
物镜有一个非常关键的参数——数值孔径。NA=nsinθ，n为介质的折射率，而θ则是进光张角的一半，也就是图上红色标注的角的一半。你直接看一张照片时它的分辨率显现不出来，但是你把它放大后就变得模糊，所以高倍镜对分辨率的要求更高，而显微镜的横向分辨率为0.61λ/NA，所以一般来说高倍镜的NA更大。

随着放大倍数的增大，色差与球差将对成像造成严重的影响，因此物镜都会有消色差、消球差的设计，而这需要引入额外的透镜。

可见高倍物镜里边的透镜数量增多，那么自然而然光在通过高倍物镜时损耗的能量增多，也就是说高倍物镜的透光率下降了，因此视野会变暗。

By Patwf

本征值，本征方程是什么？

by 匿名

微观粒子的世界与我们宏观世界有一个很大的区别，那就是在宏观世界一切似乎都是连续的，而到了微观世界则是不连续的，也就是量子化的。比如能量是一份一份的，电子绕核旋转只能处于特定的“轨道”与能级上。也就是说微观粒子并不是任何状态都能达到的，而只能处于一些特定的状态，即本征态。做实验对它进行测定时，你所能测到的数据只能是一些特定的值，这便是本征值。

对于某些简单的体系，我们可以对本征值、本征函数进行数学上的求解，也就是说通过解方程，能够求出本征值与本征函数（微观粒子的状态用波函数来描述），这便是本证方程。

从数学上讲，量子力学里的力学量是算符，它作用于某个波函数等于某个常数乘上这个波函数，这个常数便是本征值，本征值不是任意取的，对应的波函数也不是任意的，这些特定的波函数便是本征值所对应的本征函数。

量子力学有矩阵形式，此时本征值、本证方程实际上就是线性代数里边的特征方程、特征值。

By Patwf

为什么会有负温度？负温度究竟是什么？

By 上一期的广大读者

有这么一个名词，对于大部分物理所公众号的粉丝来说应该是很熟悉的（虽然不一定知道具体内容、含义，但名字是知道的），它的名字叫做——热力学三大定律。

不过除了这三大定律，还有一条定律，虽然比第一第二晚了80年但是却是非常基础的一条定律，其重要性不亚于它们，因此叫热力学第零定律。

热力学第零定律是大量实验的总结。它的表述为：两个互不接触的热均匀体系，当它们“同时”和第三个热均匀体系接触并达到热平衡时，这两个体系之间也必然达到热平衡。

也就是说，两个体系是否热平衡，并不依赖于两个体系是否在热接触。热接触可以为热平衡创造条件，但是否热平衡是由两个体系内部的热运动所决定的，这是体系本身的固有属性。

因此，处于同一热平衡状态下的体系，必然有一个共同的、能够表征他们热学特征的物理性质，这便是温度。

考虑两个处于热平衡的体系，他们一起组成一个孤立系统。那么这个系统的熵S与能量E便是两个体系的熵、能量之和，同时每个体系的熵S都是各自能量E的函数，即：

孤立系统的熵永不减小，平衡时熵最大。对这个系统来说，S在能量E给定的情况下有极大值。即E是一个常数，因此E₂=E-E₁。可见E1或E2只要有一个确定，那么另一个就确定了。

当S取极值时有：

可见对于处于热平衡的系统来说，系统中各部分S对E的导数都相同，在整个系统内部都不变。这不就是我们刚才讨论的温度吗？我们把S对E的导数定义为物体的绝对温度，严格的公式表示为：

温度有一个重要的性质：能量从温度较高的体系转移到温度较低的体系。

从数学上看，随着能量的增大如果熵也增大，那么1/T便是大于0的，也就是说绝对温度不会小于0。但如果熵对能量的导数小于0，温度不就是负值了吗？

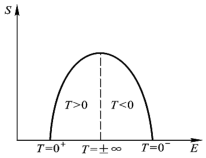
如果S作为E的函数有极大值，那么在极大值左侧T＞0，而在右侧T＜0。如图所示：

（图片来自苏汝铿《统计物理学》）

只看左半边，温度从正0度可以一直增大，一直增加到正无穷；而只看右半边时，温度从负无穷接近负0度。（负0度正0度可以理解为绝对0度的左右极限）

我们考虑一个简单的体系，这个体系只有两个能级，一个ε₁一个ε₂且ε₂＞ε₁

当体系趋于从正温度趋向于绝对0度，即0⁺，也就是我们常说的绝对零度时，体系所有的粒子都会处于低能级ε₁上，此时体系的S=0

随着温度的上升，将会有粒子被热激发到高能级ε₂上，温度越高将激发的越多。

当温度趋于正无穷时，全部的粒子都会被激发到ε₂上吗？

根据玻尔兹曼分布，粒子处于ε₁与ε₂的概率f₁与f₂有如下关系：

所以当T趋于正无穷时，f₁=f₂，也就是说有一半的粒子在低能级，一半在高能级。此时系统的熵是最大的。S最大，则S对E的导数为0，对应为S-E曲线与E轴平行，此时1/T=0，T等于正无穷。

接下来如果有办法能够让更多的粒子跑到高能级上去，则体系的熵会下降。

多一个粒子从低能级跑到高能级，则体系的能量就会增大，所以此时随着体系能量的增大熵会减小，因此1/T＜0，T便是负温度了。

当粒子全部跑到ε₂上时，粒子出现在ε₂上的概率为1，而处于ε1的概率为0，因此f₂/f₁趋于正无穷，从上边的公式可以看出来因为ε₂＞ε₁所以T要趋于负的无穷小，即0^-

从T=0^-往左靠，越多的粒子将处于ε₁上，所以f₂/f₁的比值便会从正无穷开始减小，当T等于负无穷时，f₁=f₂，此时体系与T等于正无穷时有相同的分布以及相同的热力学量。因此温度的负无穷与正无穷在物理上是恒等的。以上便是关于负温度的介绍、以及对那副图的详细解释。

温标是可以任意选择的，如果定义一个新的温标：

则T从0⁺到无穷再到0^-对应与θ的变化是单调的从负无穷到正无穷。绝对0度不能达到可以解释为θ不能达到无穷。下边这个图能够让大家更直观的理解：

（图片来自苏汝铿《统计物理学》）

只要能级的数目有限，并且最高的能级有上界，就有可能出现负温度。负温度的实验现象最早是珀色耳和庞德在核自旋体系中发现的。他们把LiF晶体在强磁场中磁化，然后让磁场迅速反向。由于在这种晶体中核自旋相互作用的弛豫时间τ₂ 远小于自旋和晶格之间相互作用的弛豫时间τ₁，因而有可能出现体系处在其总能量高于平均能量的状态的情况。

最后我们再来说一下为什么负温度比任何正温度都要高。

从热激发的角度来看，随着温度的增高更多的粒子处于高能级，但即便温度达到正无穷，也只能有一半的粒子处于高能级，而负温度下处于高能级的粒子数目比温度为正无穷要多，所以负温度的热激发能力比正无穷的温度要强。

从热平衡角度来看，负温度实现了粒子数的反转，熵随能量增多趋于减少，因此是不稳定的，有能量减少、熵增大的趋势。将负温度的体系与任何一个温度为正的体系接触，负温度体系都将受到扰动，进而粒子会从高能级跑去低能级，而减少的能量则传递给了与它接触的体系。因为能量只能从高温物体传递给低温物体，所以负温度比任何正温度都要“高温”。

By Patwf