赠书 | 你不可不知的 π

#福利# 为庆祝 PI DAY, [遇见] 联合图灵社区给支持的朋友们送出 26 本好书, 详见文末. 

π的一百万位有多长? (英文字幕)

下文节选自《你不可不知的 50 个数学知识》, 已获人邮图灵授权许可, [遇见数学] 特此表示感谢! ★提示: 如果文中数字/公式显示较大, 请点击右上角中"刷新"即可恢复正常. 

 是数学中最著名的数。 忘记自然界中所有其他常数也不会忘记它，  总是出现在名单中的第一个位置。如果数字也有奥斯卡奖， 那么  肯定每年都会得奖。

 或 pi， 是圆周的周长和它的直径的比值。它的值，也就是这两个长度之间的比值，不取决于圆周的大小。无论圆周是大是小， 的值都是恒定不变的。  产生于圆周中，但是在数学中，它却无处不在，甚至涉及那些和圆周毫不相关的地方。

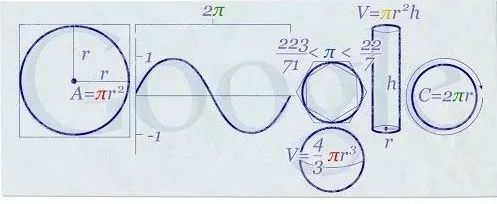
2010年圆周率日的 Google Doodle

▌锡拉库扎(Syracuse)的阿基米德人们在古时候就对圆周周长和直径的比值产生了浓厚的兴趣，在公元前2000年左右，巴比伦人发现了周长大约是直径的三倍。

关于  的数学理论，真正开始于锡拉库扎的阿基米德，大约在公元前225年左右，阿基米德就是在那里完成他伟大的创举的。数学家们喜欢评价同行的等级，他们认为阿基米德可以与卡尔·弗里德里希·高斯（数学王子）和艾萨克·牛顿齐名，不管这种评价有何价值，阿基米德应该位列任何数学名人堂中是毋庸置疑的，但是他并没有被完全处于数学的象牙塔里，他对于天文学，数学物理学也都有很高的造诣，他还设计了战争武器，例如弹射器，杠杆，以及一种火镜，这些都是为了不让罗马人进犯. 但是据说他身上具有教授们所常有的心不在焉的特质，否则当他发现了流体静力学中的浮力定律时是什么使得他从浴盆里跳出来，连衣服都不穿，就冲到大街上大喊“Eureka”（拉丁语“我发现了”）？但是我们找不到关于他如何庆祝  的发现的记录。

当把  定义为周长和直径的比值后，如何进一步计算圆的面积呢？通过推导，可以得到半径为  的圆的面积为  , 或许这一点比周长/直径给出的定义更加有名.  对周长和面积的双重职责是非常重要的.

这个结论是如何证明的呢？周长可以被切分为很多狭长的三角形底边边长为 ，高度近似为半径 . 它们在圆内部形成了一个多边形，圆的面积可以近似为这个多边形的面积，让我们首先将圆划分成 1000 个三角形. 推导过程都将是近似操作. 我们可以将每对相邻的三角形，拼成一个矩形(近似地), 它的面积为 . 那么整个多边形的面积将是 . 由于  约等于半圆的周长，它的长度是  , 在整个多边形的面积为，。划分的三角形越多，近似值会越接近实际值. 最后在极限上我们可以得出圆的面积为 。

阿基米德估算出  的值处在  和  之间. 正是因为阿基米德，我们有了大家所熟知的  的近似值 . 关于设计  这个符号的荣誉要归功于很少人知道的威廉·琼斯, 他是一个威尔士数学家, 在18世纪成了伦敦皇家学会的副主席. 物理学家和数学家欧拉在圆周率的使用中将  推广开来。

▌ 的精确数值
我们永远无法知道  的精确数值，因为它是一个无理数，这一点被约翰·兰伯特于1768年证明.  的小数展开是无穷无尽的，并且没有可预测的模式，它的前 20 位是3.1415926535897932384... 中国数学家所采用的  的数值为:3.16227766016837933199, 这个值在公元 500 年左右被婆罗摩笈多所采用. 事实上，这个只比 3 这个粗略近似值要好一些，它和  相比，它和  相比到小数点后第二位才不相同。
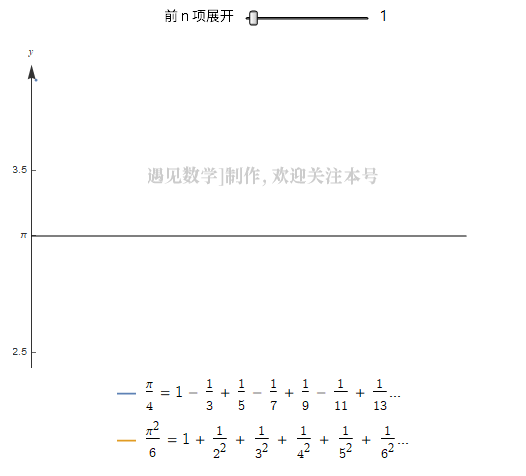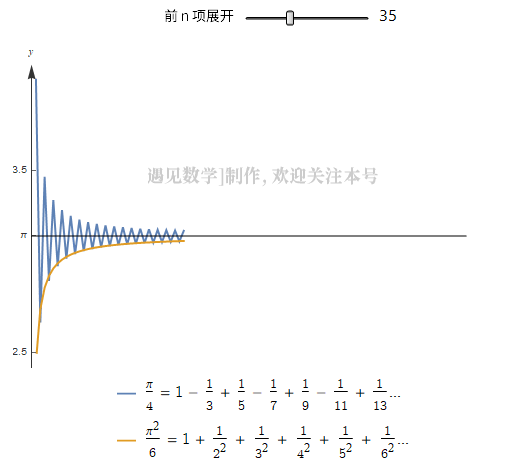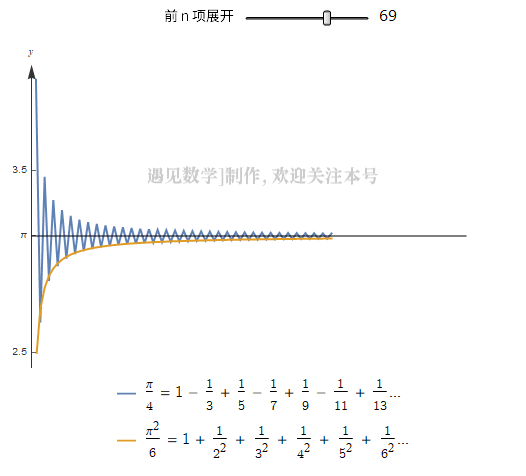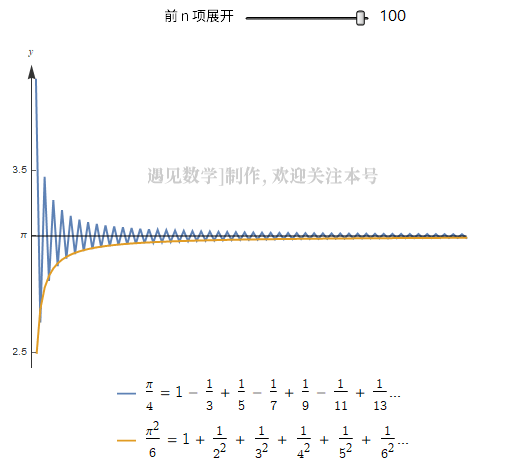
 可以从一个数列计算。 一个著名的数列展开式是


但是这个数列需要一个很痛苦漫长的过程，才能收敛到 , 计算是几乎不可能的，欧拉找到了一个可以收敛到  的重要序列:

上面两种级数展开前 100 项的收敛过程

自学成才的天才拉马努金想出一个漂亮的  的近似公式. 这个式子里仅涉及 2 的平方根:

数学家对  是如此的着迷, 当兰伯特证明了它不可能是分数的时候，德国数学家林德曼在 1882 年解决了一个关于  的最重要问题. 他证明了  是 "超越"(Transcendental) 的, 既  不可能是代数方程(一个仅含  的指数项的方程)的解. 通过解决这个千古之谜，林德曼给出了"变圆为方"这一问题的结论，此问题为: 给定一个圆，如何利用一对圆规和直尺，构造一个和它面积一样的正方形. 林德曼最后证明了，这是不可能做到的. 如今化圆为方，就代表办不到的事情。

对于  的精确计算快速发展着。 1853 年, 威廉·尚可斯宣称已经将它精确到了 607 位(实际上只精确到了 527 位). 在当代，计算机给予了将  精确到更多位的新的动力，1949年， 被精确到了小数点后 2037 位. 这是由 ENIAC 计算机经过了 70 个小时的计算完成的，到了2002年  已经精确到了令人咋舌的 124100000000 位, 而且这个数还在继续增长. 如果我们准备写出  的精确值，尚克斯的计算结果仅仅需要 14 米，而2002年得到的这个结果，足可以绕地球大约 62 圈。

人们提出并解答了关于  的各种问题， 的这些数字是完全随机的吗？有没有可能预测它的展开式里有一段序列? 例如，有没有可能在展开式中出现 0123456789 这样的序列，在20世纪50年代，人们认为这个问题是不可知的，人们在  上已知 2000 位展开式中没有找到这样的序列. 荷兰数学界的领军人物鲁易兹·布劳威尔认为这个问题毫无意义，因为他相信这个序列是不可能出现的，事实上，这个序列在1997年被找到了，它开始于第 17387594880 位, 或者按照上面那个比喻，它所在的位置差 5000 公里就绕完地球整一圈了. 你可以在仅仅一千公里后就可以发现 10 个连续的 6, 却要再绕地球一圈后再走6000公里才能找到 10 个连续的 7。

▌ 的重要性
知道  的这么多位有什么用，毕竟大多数计算机仅仅需要小数点后几位就够了，对于绝大多数实际应用来说，或许十位以内已经足够了，而阿基米德的近似值  也可能对大多数情况都已经足够好了. 但是, 对于  的广泛展开绝不是仅仅为了娱乐. 他们除了能使那些自称为" 的朋友"的数学家们神魂颠倒外，还可以用于测试计算机性能极限。

或许关于  最离奇的一段故事是，印第安纳州立法院曾经试图通过一条议案，以固定它的数值. 这个故事发生在19世纪末，一个名叫古德温的医学博士，提出一条议案，希望将  变成"易理解的". 而这条议案面临的实际问题是: 提议者自己却没有能力知道他想要固定的值是多少. 值得庆幸的是, 在议案通过之前，他们意识到了对  进行立法是一件多么荒唐的事情. 从那一天起，政客们便远离了 。 (完)

PI DAY 赠书

每种书赠出 2 本, 说说你最中意那本书并说说理由, 活动截止本周六23:59分.
✪注意, 第3,10,11种书只限[遇见翻译小组]核心群朋友们参加, 其余书籍没有限制.

1. 春夜十话：数学与情绪

我们通常认为，数学是逻辑性的学问，而日本数学家冈洁先生却认为，数学中最重要的是“情绪”。

情绪是影响心智与认知发展的重要因素，若不能培育“健全的情绪”，则很难真正理解数学和创造性是什么。本书从“情绪与心智”的角度，论述了认知发展、义务教育中的深层问题，同时阐述了对人性的细微考察与独到理解，是一本影响了日本几代人的经典名作。

2. 神奇的数学

牛津大学的马库斯·杜·索托伊教授常年主持青少年数学科普讲座，擅长借助孩子们感兴趣的话题，引出无所不在的数学知识。在本书，你会了解到神秘莫测的质数、变化多端的形状、游移不定的概率、深藏不露的密码、能掐会算的预测术，每章还会介绍一个悬赏百万美元的著名数学难题，仿佛向读者指示一条通往数学科学巅峰的攀登之路。

3. 数学万花筒+数学万花筒2+数学万花筒3：夏尔摩斯探案集

本套书是伊恩·斯图尔特教授五十多年收藏的精选，包括有趣的数学游戏、谜题、故事和八卦的大杂烩。大部分内容独立成篇，你可以从几乎任意一处着手阅读。除去可以了解各种有趣的数学知识和八卦，你还可以亲自参与到数学当中，亲自制作数学游戏，试着解决数学谜题。作为参考，本书最后给出了那些有已知答案的问题的解答，以及一些供进一步探索的补充说明。

4. 简单微积分

本书为微积分入门科普读物，书中以微积分的“思考方法”为核心，以生活例子通俗讲解了微积分的基本原理、公式推导以及实际应用意义，解答了微积分初学者遭遇的常见困惑。本书讲解循序渐进、生动亲切，没有烦琐计算、干涩理论，是一本只需“轻松阅读”便可以理解微积分原理的入门书。

5. 数学思考法

本书为讲解“数学思考法”的通俗科普读物，书中通过用数学思维解析实际生活案例、公众认知中的错误直觉、数学经典名题等方式，由浅入深地传授了分析数据信息价值、辨别谎言、拆解转化复杂问题、抓住事物本质的思考之法，同时讲解了相关的数学知识与理论，可以有效提高理性思维、判断与解决问题能力，对于理解数学、培养数学兴趣亦有有益启示。

6. 陶哲轩教你学数学

本书是国际知名数学家陶哲轩15岁时的著作，从青少年的角度分析数学问题，主要是数学竞赛等智力谜题，用学生的语言解释思考过程，完整展现了少年陶哲轩的解题思路。本书启发性强，既能激发学生的数学兴趣、培养思维逻辑，又能充分展现数学的魅力。

7. 计算进化史

本书从计算的演变这一独特视角回顾了数学、逻辑学和哲学的历史沿革，展望了计算机科学为数学带来的全新前景，以及由此引发的自然科学与哲学领域的重大变革。

8. 度量：一首献给数学的情歌

本书分为两个部分，分别介绍了对形状和运动的度量。作者以平实的语言将几何学和微积分的复杂概念以及两者之间的精妙关联解释得清晰易懂，生动展示了数学家都在做什么，以及他们为什么要这么做。

9. 算法小时代

算法与人工智能是当下最热门的话题之一，技术大发展的同时也引发了令人忧心的技术和社会问题。本书生动介绍了算法的数学原理和性质，描述了算法单纯、本质的功能，分析了算法和人工智能对人类社会现状及未来发展的影响力及其成因。

10. 普林斯顿微积分读本（修订版）

本书阐述了求解微积分的技巧，详细讲解了微积分基础、极限、连续、微分、导数的应用、积分、无穷级数、泰勒级数与幂级数等内容，旨在教会读者如何思考问题从而找到解题所需的知识点，着重训练大家自己解答问题的能力。本书适用于大学低年级学生、高中高年级学生、想学习微积分的数学爱好者以及广大数 学教师。本书既可作为教材、习题集，也可作为学习指南，同时还有利于教师备课。

11. 线性代数应该这样学（第3版）

本书强调抽象的向量空间和线性映射, 内容涉及多项式、本征值、本征向量、内积空间、迹与行列式等. 本书在内容编排和处理方法上与国内通行的做法大不相同, 它完全抛开行列式, 采用更直接、更简捷的方法阐述了向量空间和线性算子的基本理论. 书中对一些术语、结论、数学家、证明思想和启示等做了注释, 不仅增加了趣味性, 还加强了读者对一些概念和思想方法的理解。