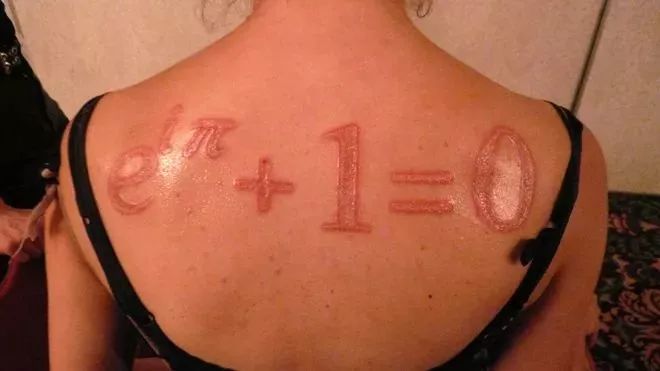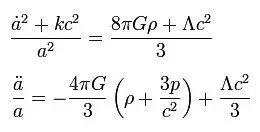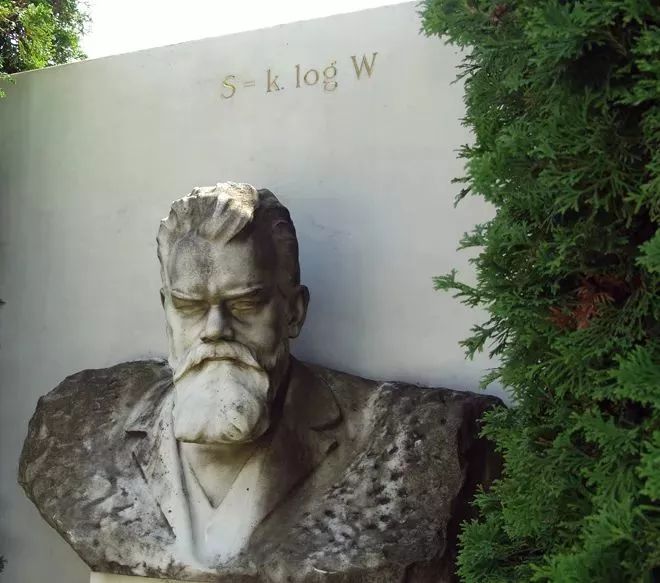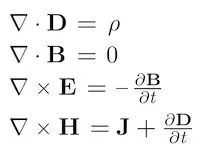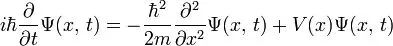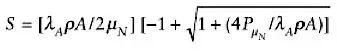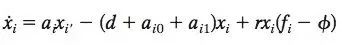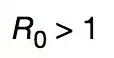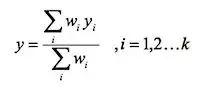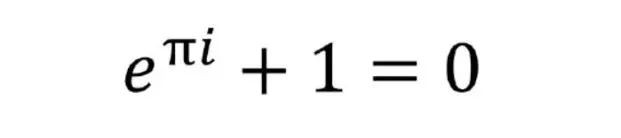九大公式身上纹,那才叫“社会”!
我们一生中总会遇见各种各样复杂的公式,这些公式中掺杂着多个积分、微分、连乘、求和等数学符号,但实际上,世界的复杂性是建立在一些简单公式的基础上的。下面我们先来回顾之前连线网站(wired.com)评选出的9大geek们应该了解的公式,如果记不住的话就纹在皮肤上!
01
最美的公式:欧拉恒等式
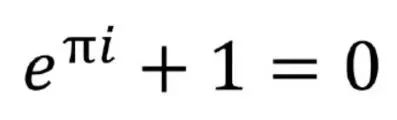
理论物理学家理查德·费曼非常喜爱这个公式,他将其称之为“宝石”和“无与伦比”的公式,现代人则将它称之为“最美的公式”。
02
描述宇宙的模型:弗里德曼方程
图中的两个弗里德曼方程源于爱因斯坦的广义相对论,它描述的是宇宙从炙热的大爆炸诞生之际,到冰冷的快速膨胀死亡期之间整个宇宙的模型。
这个公式中有一个名为宇宙学常数的奇怪符号Λ,它最早由爱因斯坦引进,由于当时认识的局限性,爱因斯坦认为宇宙应该是静止的, 所以他引入宇宙常数作为排斥力来抵消重力,从而保持整个宇宙处于恒久不变的静态。但随后的观测显示,宇宙实际上是膨胀的。在得知哈勃的“宇宙在膨胀”理论后,爱因斯坦承认,在研究中加入宇宙学常数是他犯下的最大错误。而有一些研究则为爱因斯坦进行了辩护,因为研究显示存在一种未知的名为暗能量的神秘力量正在加速宇宙的膨胀,而这种力量则很有可能就来自宇宙常数的排斥力。
03
熵:玻尔兹曼方程
方程紧密描述了熵(S)和系统中无数粒子间(k*logW)的关系,其中,k是玻耳兹曼常数,W是热力学几率,描述的是一个系统中的微观状态数。
04
电磁学:麦克斯韦方程组
詹姆斯·克拉克·麦克斯韦在1861年最先写出了这个方程组,它描述了所有已知的电场和磁场的行为和关系,如一个移动的电荷会产生一个电磁场而一个移动的电磁场也会产生一个电场。
Z machine,位于美国山迪亚国家实验室世界上最大的X射线发射器
05
不确定性:薛定谔方程
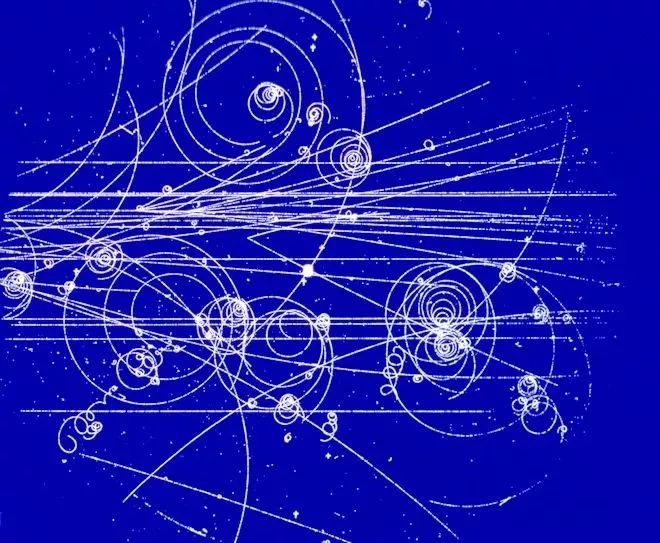
奥地利物理学家欧文·薛定谔著名的薛定谔方程是宇宙中微观粒子的基本方程,它阐述了在势场的作用下,亚原子微粒是如何随着时间变化的。量子力学中描述微小颗粒采用的方法是波函数,其中,原子和粒子的波函数可以描述它们何时何地出现的概率。
但是,在量子力学创立初期,物理学家们对如何解读薛定谔方程中的波函数起了争执。一些人认为波函数不存在真实的物理意义,它仅仅是一个有用的计算工具;其他人则认为,波函数表明我们是无法完全认识宇宙的。还有人认为,我们在测量粒子之前,只有波函数知道电子在空间的概率,而一旦我们测出了,该电子的波函数就会在测量的瞬间坍缩,但是薛定谔并不同意“粒子一旦测量了波函数就会坍缩”的解读,他著名的薛定谔猫实验则就是为了证明这种解读是存在不足的。
在氢泡室中亚原子粒子的鬼魅路径
06
生命就是一座岛:岛屿生态地理学
尽管物理学家们可以从不同角度阐述宇宙的膨胀,但是对地球上最基本的生命,我们却很难为此量化。在20世纪后期,生物学家总结出了岛屿生态地理学理论,这个理论描述的是岛屿中动物种群的动态平衡。
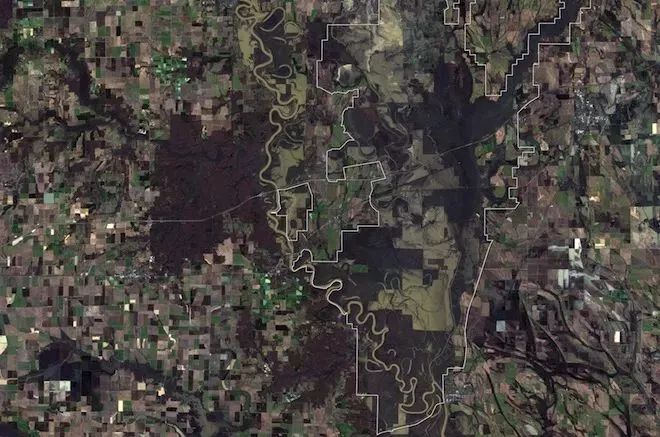
公式左边是给定岛屿能够支撑的动物物种数,公式右边是动物丰度、有效面积和迁入迁出的比例。这个理论并不局限与海中于世隔绝的岛屿,它尤其适用于那些被人类活动孤立的生态系统。几乎所有的物种都生存在由人类定义的除了两极以外的岛屿中,而最大的岛屿毫无疑问就是我们的地球了。
阿肯色州的Cache河保护区,在这片被孤立的湿地里常有人报道说看到灭绝的象牙喙啄木鸟
07
演化的本质:诺瓦克的可演化性
从最本质的层面来说,生命就是不断的自我复制,那么,生命是如何开始的呢?这有点像终极版的先有鸡还是先有蛋难题,很难得出确切答案。哈佛大学数学家和生物学家马丁·诺瓦克一直致力与将生命的起源问题简化成最简单的化学系统,以便用数学公式来描述,可演化性公式就是他的成果之一。
公式左边代表的是分子所有可能的字符串(因为他用0和1来表示最早期生命的化学组件),公式右边是化学反应的速度、形成短串概率大于长串的倾向、进化中的选择压力和适应等级。如诺瓦克所示,若想要出现生命,分子必须经过自然选择和突变的过程。如果能够满足这些情况,那么自我复制这个过程就会顺理成章的出现了。
加里福利亚莫诺湖的日出场景,莫诺湖是一个酷热、缺氧、富砷的湖泊,科学家们认为这很像早期的地球
08
疾病爆发的边界:基本传染数R₀
09
性不性感:美貌的数学公式
不是所有事物都可以量化的,尤其是你想量化人心或者思想的时候,你根本无从下手。数十多年来,物理学家和生物学家一直在尝试用数学公式来表征人类的相貌,可惜的是,即使测试了数百人对相貌的喜好偏向后,出现了一些共有的偏好,但情人眼里出西施,人们还是无法预测个体对美貌的偏好。
一位以色列计算机科学家用程序来量化脸部的吸引力后,得出了这个公式。公式左边的y是由经验得出的相貌得分,公式右边是使用多种测量方法测得与平均面孔对比的差异程度。
看完上面这些牛光闪闪的公式,过不过瘾?
问题来了,这些公式大多数人难有机会用到,所以光知道几个式子实在没什么意思。但是,好在它们是如此强大,以至于每个都有许多精彩故事和神奇用途,比如有公式甚至能算出你有多漂亮。
所以,就让我们从中选择几个最有意思的,讲述那些神奇的故事。或许看完你还是不会用这些公式,但至少也能说得头头是道了。
1
欧拉公式
所有没有欧拉公式的公式排行榜都是不专业的,即便对欧拉公式的介绍已经够多够多了,在这里依然不敢抹去它。让我们再次看看它是怎样用三个最基础的运算,把数学中最神奇的三个常数以及最根本的两个数联系在一起的吧。
数学中最基本的5个常数——0、1、圆周率π、自然对数的底e和虚数单位i,以及数学中最基本的两个符号,等号和加号,就这样通过一个简单的恒等式联系在了一起,实在是让人叹服。
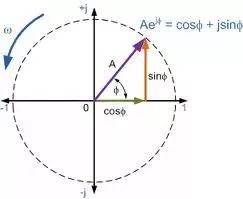
这个等式有个一几何的直观解释。一个实数在实数轴上可以用一个向量表示,旋转这个向量,就相当于乘以一个虚数i。据此建立一个以实数为横轴,虚数为纵轴的坐标系。实单位向量,每次逆时针旋转π/2, 可以分别得到结果1,i,-1,-i,1. 即转4次以后就回到了原位。而当实单位向量保持长度不变旋转θ角度,得到的向量就是:cosθ+isinθ。根据欧拉公式e iθ= cosθ+isinθ可以看出e iθ就代表实单位向量1旋转θ角后而得到的向量。所以e iπ 意味着单位向量逆时针旋转了π,结果显然是-1。
2
麦克斯韦方程
如果没有麦克斯韦方程,现在我们在邮局看到的可能还是一排排的鸽笼。而至于上微博、发短信这样的事情更是想无可想。因此也有人评论说,麦克斯韦对基础自然科学的贡献仅次于牛顿和爱因斯坦。
这个著名的方程组共有四个方程,分别是:
高斯定律(描述电荷如何产生电场)
高斯磁定律(论述磁单极子不存在)
法拉第感应定律(时变磁场产生电场)
麦克斯韦—安培定律(电流和时变电场产生磁场)
1865 年,麦克斯韦在他的论文中首次提出麦克斯韦方程组的概念,并预言了电磁波的存在,推导出电磁波的速度与光速相同(他甚至还预言了光是电磁波的一种)。麦克斯韦方程优美的特性和简洁的表述让年轻的赫兹坚信麦克斯韦关于电磁波的预言是正确的,在麦克斯韦去世 9 年后( 1888 年),赫兹终于通过实验证实了电磁波的存在。他在实验中甚至观测到光电效应,但只是记录下了这一现象,并未深入研究。 1895 年,意大利人马可尼发明了无线电报并将其商用,书面信息终于可以不依靠(传统意义上的)物质载体而存在,并能够以光速瞬时传遍全球。
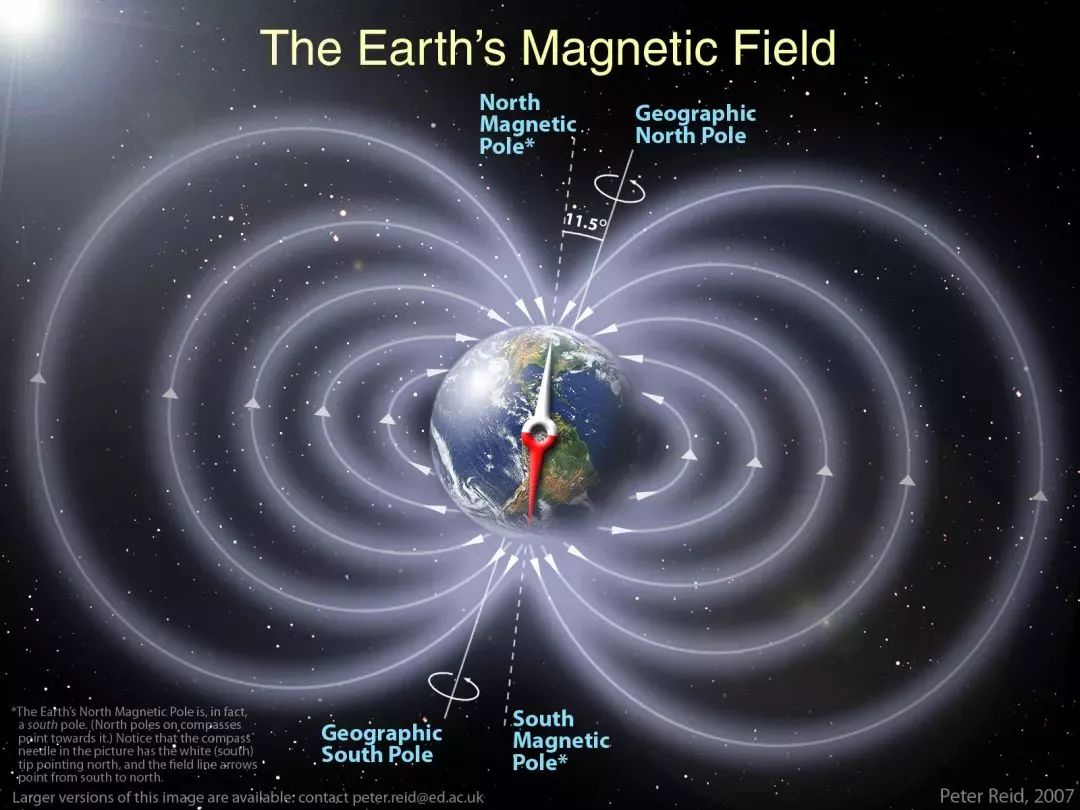
根据方程组第二个方程,即高斯磁定律,物理学家们推断出磁单极子是不存在的。我们知道,磁铁都有 N 和 S 两极,如果将磁铁从中间截断,两块新磁铁也各有两极。那么存在只有一极的物质吗?在弦理论中,将这样的基本粒子称为磁单极子,狄拉克在 1931 年首次预测了磁单极子存在的条件,大统一理论也需要磁单极子的存在作为基础。遗憾的是,直到目前为止并没有证明磁单极子存在的直接证据。在《生活大爆炸》第二季中,谢耳朵和他的朋友们前往北极就是为了寻找磁单极子存在的证据。如果磁单极子真的存在的话,那么麦克斯韦方程组的第二个和第三个方程都要相应地修正。
地球磁极,图片来源:blogspot.com
3
薛定谔方程
1900 年,物理学界一片歌舞升平,开尔文男爵在一场讲演中说,物理学将不会再有任何发现,剩下的只是精益求精的测量。但他同时也指出,在物理学的晴空中还飘着两朵小乌云——以太风的观测失败(后来证明以太事实上不存在)和黑体辐射公式的紫外灾难。但正是这两朵小乌云,彻底颠覆了传统物理学,并催生出 20 世纪物理学的两个最重要的主题——相对论和量子力学。而维也纳物理学家薛定谔提出的薛定谔方程则是量子力学领域的基础性理论之一:
其中 Ψ 是波函数,而|Ψ|^2就表示一个粒子在空间 x 和时间 t 出现的概率,这在经典物理中是不可想象的,一个粒子在要么在这里要么在那里,怎么会以概率的方式出现?就连薛定谔本人在提出这个方程时也对 Ψ 的含义也不甚了了, 1927 年波尔和海森堡提出了哥本哈根诠释(注意,这只是一个“诠释”),认为 Ψ 表示波函数,并引入概率的概念,成功地解释了薛定谔方程。但薛定谔始终也无法接受这样的解释,他用思想实验“薛定谔的猫”来归谬:一只猫怎么可能随时死去活来?而爱因斯坦对哥本哈根诠释的评价更直接:“上帝不掷骰子!”
要说的是,薛定谔提出该方程时已经将近 40 岁,也算是大器晚成的科学家。根据野史的说法,法国“官二代”德布洛意玩票去读了物理博士,临近毕业时毫无建树,听说爱因斯坦和普朗克弄出了一个叫做“光的波粒二象性”的时髦说法,一拍脑门写了一篇只有 1 页多的博士论文,称任何物质都有波粒二象性。但学术委员会也不是吃素的,这样的论文怎能通过教授们的法眼?但德布洛意的导师郎之万将这篇论文寄给了爱因斯坦,爱因斯坦客气地回信说此想法很有新意云云,这让德布洛意顺利过关。按照惯例,这篇论文被寄送到欧洲各个大学,在苏黎世大学,学霸德拜将这篇论文交给默默无闻的薛定谔讲师,让他在两周之后的讨论班给大家讲讲。薛定谔看得云里雾里自然也讲得一塌糊涂,德拜听后不甚满意,却没有直接批评薛定谔,随口说到,既然物质都是波,那总要有个波动方程吧?薛定谔灵光一现,就写出了震惊学界的薛定谔方程。
参加第五届索尔维会议的物理学家合影(是的 ,这张照片刚刚在昨天的推送提到过)
上面的话虽有玩笑成分,但也并非都是戏说。实际上,德布洛意的确是个“官二代”,他提出了德布洛意波的概念,因此受到爱因斯坦的赞赏,薛定谔也正是受这篇论文的启发提出薛定谔方程。但其他都是小说家的演绎。德布洛意在读期间至少发表了 5 篇论文,他的博士论文长达 100 多页 。
4
基本传染数 R0
除了晦涩的物理方程,下面要介绍的两个内容就没有那么抽象了,基本传染数 R0 就是其中之一。
在传染病学中,假设一个种群是封闭的(没有迁入和迁出的个体),并且没有免疫力,那么某个个体感染疾病后,他能传染的平均个体数就被称作基本传染数R0 。
一般来说,如果 R00 > 1,那传染病就会以指数的方式爆发(由于患病的个体可能会死亡,加之种群数有限,所以最终的传播速度会显著下降)。
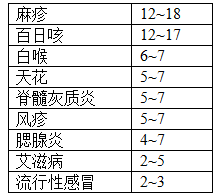
确定R0的数值对于传染病防疫决策有着重要的作用,例如香港中文大学的研究显示,2003 年爆发的 SARS 的R0指数在强力的防控措施下大约是 0.85,在没有控制的情况下为 2 ~ 3,可见有效的防控措施对于控制疫情发展有着重要的作用。根据 维基百科 的资料,常见的传染病的R0 指数为:
另外,在人口学中, R0有时也被解释为一个个体平均繁衍的后代的个数。
但由于多方面的原因,R0一般很难直接由观测得到。所以一个常见的方法是建立传染病的微分方程模型,利用数学推导的方法得到R0的数值。但这种方法也有一定的缺陷,主要是因为数学模型本身就是一个简化模型,特别是当存在交叉感染时,即便是定性的微分方程分析也相当具有挑战性。而且有时利用数学模型得到的R0尽管可以预测传染病是否能够爆发,但与传统意义上的平均传染数仍然不同。关于如何利用数学模型来研究实验中不易测量的参数也是目前交叉科学的热门课题之一,这里就不详述了。
回到传染病学的概念,那么在R0 = 1 时,疾病会不会爆发呢?一般来说我们不关心这样的情况,因为往往这个状态都是不稳定的,只要有微小的扰动就能变成一个确定的不等式。如果非要刨根问底,或许只有薛定谔的猫(如果它还活着的话)才能回答这个问题了……
5
计算你有多漂亮的公式
尽管将一切都量化听起来十分美妙,但将人类的审美完全量化听起来仍然像天方夜谭。退一步讲,即使有了将审美量化的方法,仍然无法保证这样的“美”是每个人都能欣赏的。
以色列研究人员提出了一种算法来研究“最具吸引力的脸庞”。这个算法利用计算机分析经过预先打分的人类面部图像。计算机学习这些数据后,就能够为新的面部图像进行吸引力评分。
他们的理论基础是,近年来的研究显示,人类面部的吸引力是超越种族、国家和文化的,因此应当存在普适性的(面部)审美标准。研究人员利用下面的公式进行回归分析:
其中 y 是某个图像的分数, yi 是临近的图像,而 wi 则是对应的权重。经过实测,利用该算法为面部图像打分的结果与人类打分的结果最高有 0.65 的相关性。尽管这一数字还不够理想,但仍然提供了一个新的研究方向。
各个分数段的标准长相。图片来源:wired.com
好了,最后来比照一下,你觉得自己是哪个分数段的呢?😏
作者:疯子精灵王 Fishingsnow physixfan
编辑:晓岚
参考资料:
https://www.guokr.com/article/79111/
https://www.guokr.com/article/79144/
https://www.guokr.com/article/55381/
来源:果壳科学人
编辑:X.B.Liu
近期热门文章Top10
↓ 点击标题即可查看 ↓
2. 原来,这些我们都默认科学家早已解决了的问题,至今仍然无解
4. 鸡蛋从高空坠落能砸死人,为什么猫却摔不死?科学告诉你答案
5. 光学3分钟:从入门到放弃
6. 光速为什么如此重要?