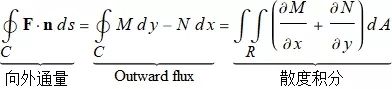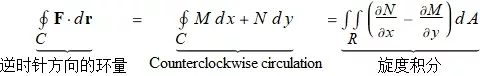【平面的格林(Green)定理】图解高等数学-下 24
关注遇见数学, 遇见更精彩的自己
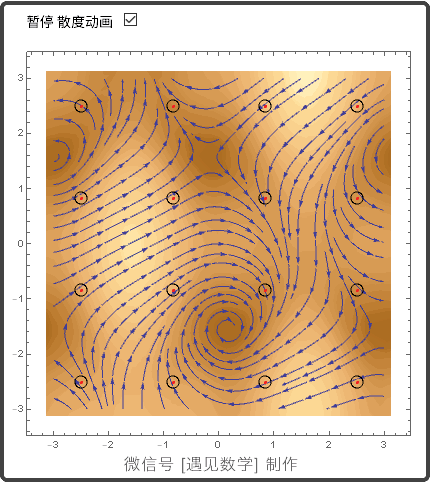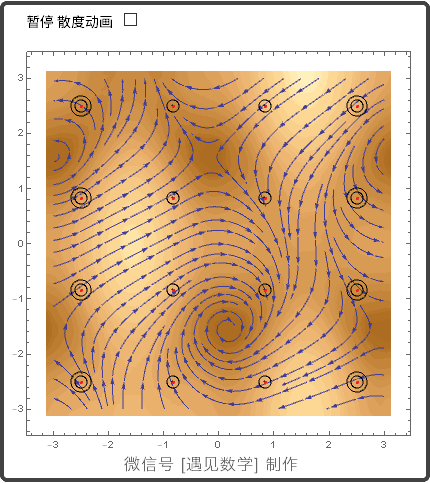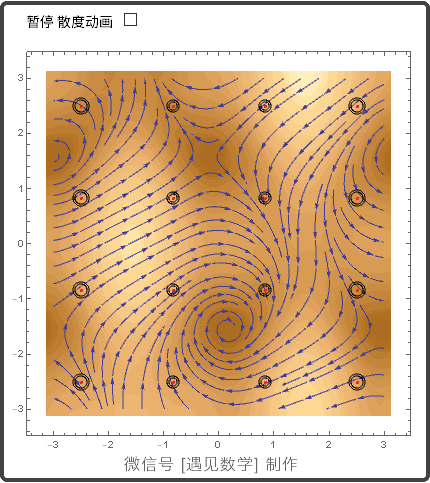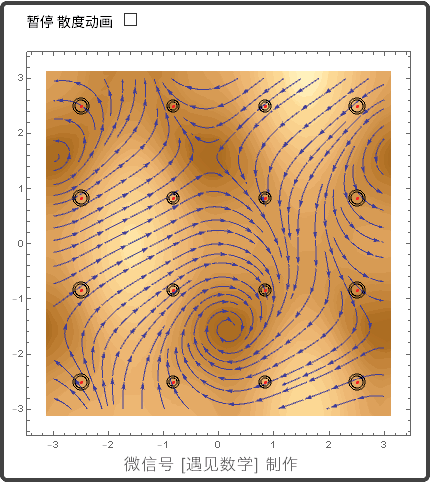
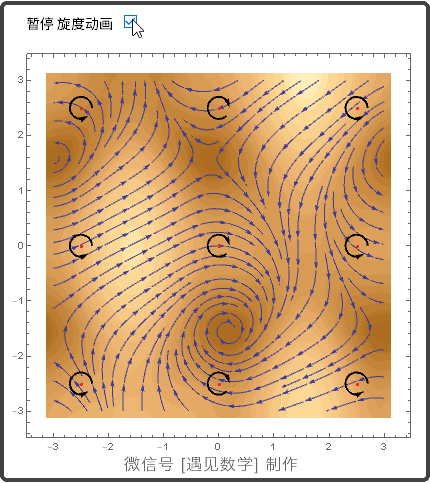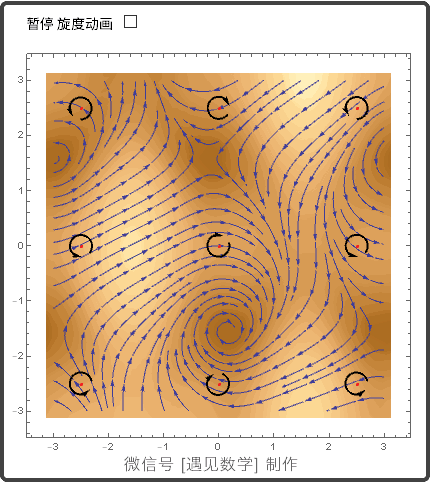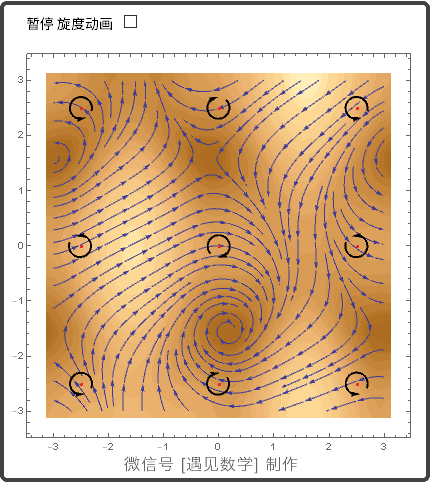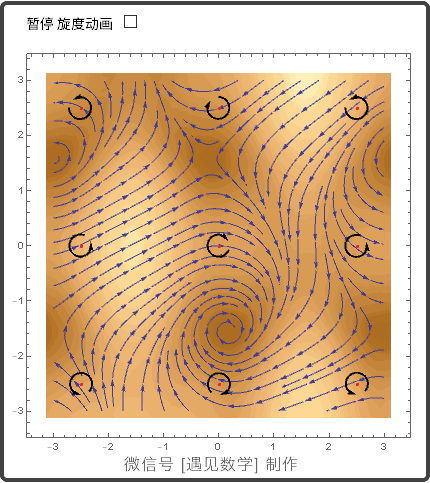
13.4 平面的格林(Green)定理
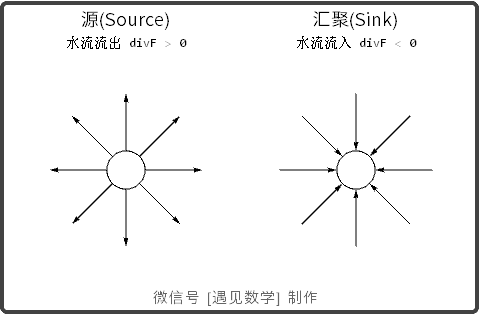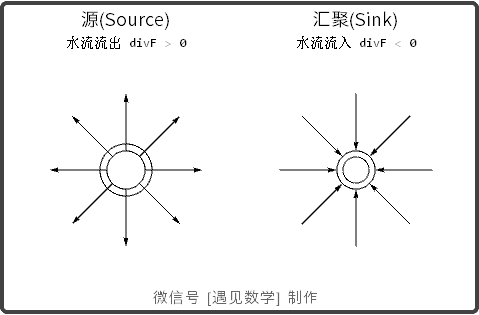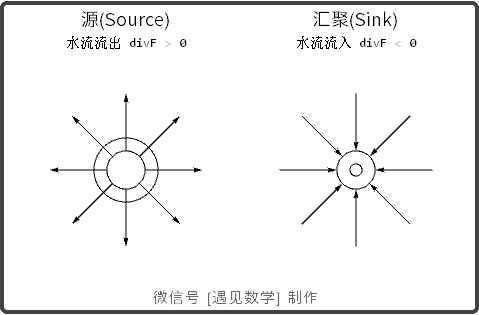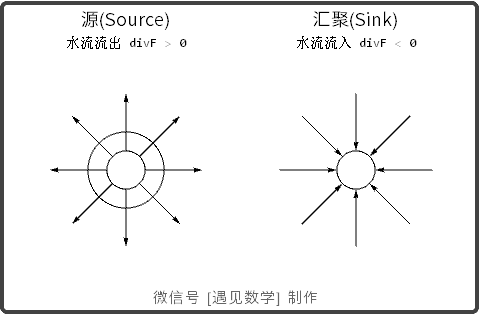
散度(Divergence)
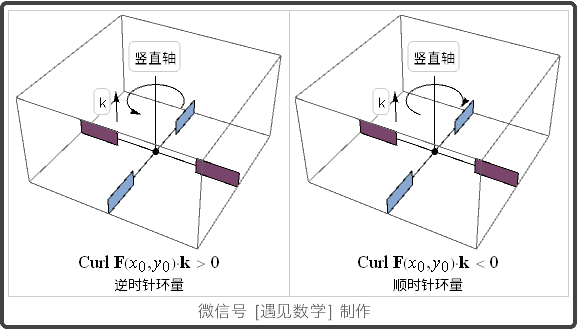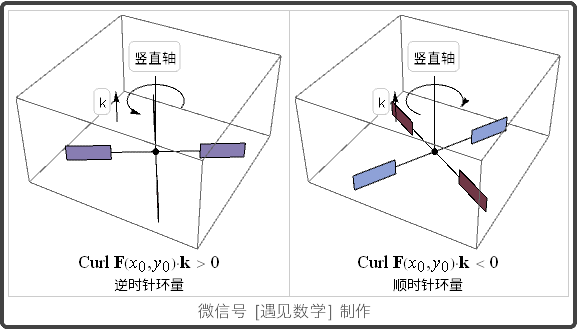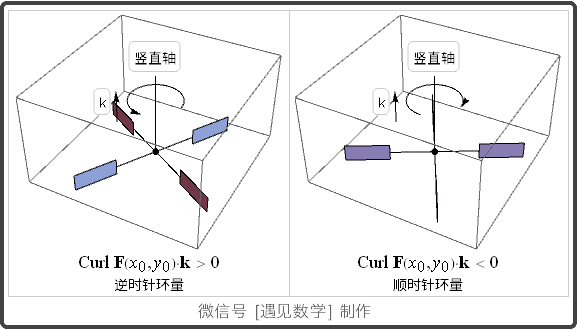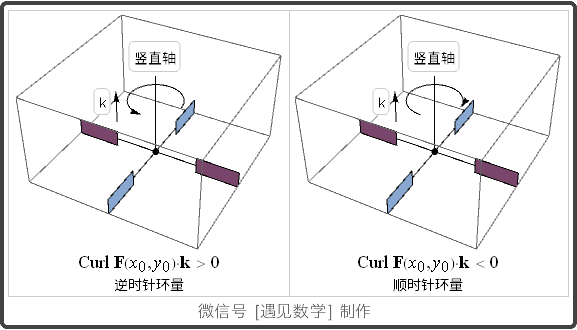
在一点的环量密度: 旋度的 k-分量
格林定理的两种形式
Green 定理(通量 - 散度形式或法向形式)
Green 定理(环量 - 旋度形式或切向形式)
登录查看更多
相关内容
Arxiv
5+阅读 · 2018年7月23日
Arxiv
5+阅读 · 2018年1月26日