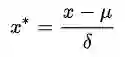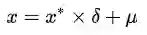不加载任何包，手撕一个R语言版BP神经网络模型

作者：梁凯  R语言中文社区专栏作者

知乎ID：https://www.zhihu.com/people/liang-kai-77-98

前言

大家好，很久没写文章了，这段时间俗事缠身，忙于俗事，愧对于自己的研究，抛开精虫上脑般的资本，对于一个立志于发展新技术新科技，乃至立志于理论研究的人来说，只有勤勤恳恳，埋头苦干的做好理论研究，把研究转化为技术才是人工智能发展的正道，而不是一心想搞个大新闻，吸引点融资然后不了了之。本人还是认为未来是AI的世界，AI everywhere，但是也不像个别媒体打了鸡血般的吹上了天，脚踏实地的为这个新科技做点贡献才是我辈中人该做的。好了废话不多说，今天为大家带来的是不加载任何包，手撕一个神经网络，实验数据集是用烂了的波士顿房价。python版的神经网络网上有很多，但是R版的很少，在这里需要感谢，中科院自动化研究所钱鸿博士和清华大学张阳阳博士的倾情答疑，神经网络的基本知识这里就不再重复讲了，BP算法也不着重讲了，这里主要讲解怎样用R语言不加载任何包的情况下，构建一个神经网络，代码结构是基于python版本的，但是是用R重构的，通过这样的对比能让各位更加清晰的了解BP神经网络，以及R与python的不同点和各自的优缺点。好了下面开始讲解代码。

R和python不一样，R更倾向于科学计算语言函数编程，对于python的类class来说R模块化通常用函数来表示。

1.定义激活函数

#首先定义激活函数##############这里我们暂时定义两个激活函数sigmoid和tanh函数#############R本来就是科学计算语言不像python是万金油，python科学计算要用到numpy，而R你可以直接##############把它看成是numpy，所以它包含了tanh函数这里我们就可以不用定义Tanh函数了，但是我们##############还是要定义tanh的导数sigmoid<-function(x){    1/(1+exp(x))      }########以下是激活函数导数的定义。sigmoid_derivative<-function(x){     sigmoid(x)*(1-sigmoid(x))       }tanh_derivative<-function(x){          1-tanh(x)^2           }    

2.模块的初始化

接下来我们的模块便是初始化，这里的初始化最主要的目的有两个第一是定义激活函数函数,第二是初始化每层的权重，在这里需要注意的是对于权重来说输出层没有权重，所以从网络结构来说，例如5层（包含输出层）的权重只有四层。其次需要在输入层加上bias，也就是说以波士顿房价为例，输入层有13个，但是加上bias便是有14个输入，而且除了输出层以外每一层都必须加上各自的阈值，就和我们理论上一样每一层隐藏层都必须减去阈值。

###函数的输入有两个，layers和activation，layers就是你需要自定义的网络结构###R中网络结构输入为一组一维数组如C（13，3，1）就表示有输入层13个节点，和一个隐藏层3个节点还有1####个输出层1个节点，这里要注意的是我们面临的问题是回归问题所以只有一个输出。你也可以根据自己的需####要添加自己想要的网络结构如我就用c(13,3,3,2,1)这种网络结构表示1个输入层13个节点和1个输出层，另####外有3层隐藏层，他们分别的节点为3，3，2.init<-function(layers,activation){     if(activation =='tanh'){activation<<-tanh      activation_prime <<- tanh_derivative}     if(activation =='sigmoid'){activation <<- sigmoid      activation_prime <<- sigmoid_derivative}     ###以上是选择使用哪种激活函数，你也可以自己添加激活函数      init_weights<-list()   ###这里我们依照我们刚讲过的输出层没有权重所以必须减一     length(init_weights)<-length(layers)-1     ###这里加一是因为每层有自己的阈值      for(i in 1:(length(layers)-2)){      nrow<-layers[i]+1      ncol<-layers[i+1]+1      layer_matrixweight<-matrix(nrow=nrow,ncol=ncol,runif(nrow*ncol,-1,1))###这里我们必须要说的是R语言比较python最大的优点便是数据格式多样化，这里我们用list格式就可以建立###十分方便的三维数据，也可以用matrix格式轻易建立矩阵，这里我们用runif随机从-1到1之间筛选初始值      init_weights[[i]]<-layer_matrixweight       }      ###最后一层因为没有阈值所以结构上我们必须把他单独列出来这也就是last_ncol没有加一的原因      last_nrow=layers[length(init_weights)]+1      last_ncol=layers[length(init_weights)+1]      init_weights[[length(init_weights)]]<-matrix(nrow=last_nrow,ncol=last_ncol,runif(last_nrow*last_ncol,-1,1))      #####这里我们为了区分用init_weights建立初始权重并把它赋予全局变量以便后面的函数调用       init_weights<<-init_weights    }

3.拟合函数的编写

下面我们进行拟合函数模块的编写，从理论上我们可以证明函数的梯度就是最佳的优化方向，所以这里我们就需要层层的求出输出值，然后用输出值倒推出每一层的delta,然后再更新权重。

###这里的X和Y是训练样本fit<-function(x,y,learning_rate, epochs){     weights<-init_weights     old_colname<-colnames(x)     #加入一列1，作为bais      x<-cbind(1,x)    #######修改列名（可选）     colnames(x)<-c('bais',old_colname)     for(i in 1:epochs){     ####随机梯度下降方法SGD     n<-sample(1:length(x[,1]),1,replace = FALSE, prob =NULL)     calculate_weights<-list(x[n,])     length(calculate_weights)<-length(weights)     #######计算权重          for( k in 1:length(weights)){             dot_value<-calculate_weights[[k]]%*%weights[[k]]             activation_value<-activation(dot_value)             calculate_weights[[k+1]]<-activation_value              }                           error<-y[n]-calculate_weights[[length(calculate_weights)]]          ############从输出层反向递推计算delta           deltas<-list(error * activation_prime(calculate_weights[[length(calculate_weights)]]))               for( j in (length(calculate_weights)-1):2){                        length(deltas)<-length(deltas)+1                        deltas[[length(deltas)]]<-deltas[[length(deltas)-1]]%*%t(weights[[j]])*activation_prime(calculate_weights[[j]])                      }                ############倒转 deltas                 deltas_reverse<-list()                length(deltas_reverse)<-length(deltas)                    num<-length(deltas)                    for(m in 1:length(deltas)){                     deltas_reverse[[m]]<-deltas[[num]]                            num<-num-1                      }                 ############逐层更新权重              for(t in 1:length(weights)){                    layer<-as.numeric(calculate_weights[[t]])                    delta<-deltas_reverse[[t]]                    weights_new<- weights[[t]]+learning_rate*(layer%*%delta)                    weights[[t]]<-weights_new                    }              }               print(weights)            #######训练好的权重用fit_weights来表示             fit_weights<<-weights                      }

4.预测函数的编写

接下来就是预测函数，这里我们先写一个对每一个测试样本计算预测值的函数predict，再用apply函数写一个函数predict_total对所有的测试集并行矩阵计算预测值。

 predict<-function(x){              for(i in 1:length(fit_weights)){              dot_predict<-x%*%fit_weights[[i]]              activation_predict<-activation(dot_predict)                    x<-activation_predict                             }                       return(x)                        }                 predict_total<-function(x){                  new_x_test<-cbind(1,x)                 predict_values<<-apply(new_x_test,1,function(x)predict(x))                 print(predict_values)                  }

5.归一化

以上神经网络主体部分就已经写好了，接下来我们需要对data进行预处理，读取数据，随机选取训练集和测试机，然后进行归一化，这里介绍了标准化归一化和极差归一化。

#读取数据  data<-read.csv ('boston_house_prices.csv')###随机抽取训练集和测试集（这里取百分之七十训练集）sample_num<-sample(c(1:length(data[,1])),length(data[,1])*0.7, replace = FALSE, prob =NULL)data_train<-data[sample_num,]data_test<-data[-sample_num,]x_train<-data_train[-which(colnames(data)=="MEDV")]y_train<-data_train[which(colnames(data)=="MEDV")]x_test<-data_test[-which(colnames(data)=="MEDV")]y_test<-data_test[which(colnames(data)=="MEDV")###标准化归一x_train<-apply(x_train,2,function(x)scale(x,center=T,scale=T))y_train<-scale(y_train,center=T,scale=T)x_test<-apply(x_test,2,function(x)scale(x,center=T,scale=T))y_test<-scale(y_test,center=T,scale=T)###极差化归一（可选）#x_train<-apply(x_train,2,function(x)as.matrix( (x - min(x)) / (max(x) - min(x))))#x_test<-as.matrix( (x_test  - min(x_test )) / (max(x_test ) - min(x_test )) )#y_train<-apply(y_train,2,function(y)as.matrix( (y - min(y)) / (max(y) - min(y))))#y_test<-as.matrix( (y_test   - min(y_test  )) / (max(y_test  ) - min(y_test  )) )

6.预测

我们经过一系列计算来得到训练后的权重进行预测，评价标准为MSE和MAE。

init(c(13,3,3,2,1),"tanh")fit(x_train,y_train,0.001,20000)predict_total(x_test)

最后再啰嗦几句，这里我们求得的预测值是标准化过后的，所以我们必须要根据公式对归一化的数据进行还原，python可以用sklearn包，但R不加载任何包可以自己写,以标准化归一为例。

公式为：

其中μ为所有样本数据的均值，δ为所有样本数据的标准差，所以可以求得：

7.预测数据还原

###注意这里我们因为还原预测数据所以对应的就是y_train,其实y_train_inverse就等于原始的###y_train值同理y_test也等于归一化之前的y_testy_train_inverse<-as.matrix(data_train[which(colnames(data)=="MEDV")])y_test_inverse<-as.matrix(data_test[which(colnames(data)=="MEDV")])predict_inverse<-predict_values*sd(y_train_inverse)+mean(y_train_inverse)mse<-mean((y_test_inverse-predict_inverse)^2)mae<-mean(abs(y_test_inverse-predict_inverse))

8.结果

mse[1] 29.52206> mae[1] 4.212332

结论：

可以看出结果不是很理想，但是我们可以继续调参或者做另外的trick，另外我们的程序也可以写得更快写，少些for循环多写矩阵计算，下次我们将更改程序，使它更加强大。

公众号后台回复关键字即可学习

回复 爬虫             爬虫三大案例实战  
回复 Python        1小时破冰入门

回复 数据挖掘      R语言入门及数据挖掘
回复 人工智能      三个月入门人工智能
回复 数据分析师   数据分析师成长之路 
回复 机器学习      机器学习的商业应用
回复 数据科学      数据科学实战
回复 常用算法      常用数据挖掘算法