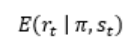干货｜浅谈强化学习的方法及学习路线

2018 年 3 月 28 日 机器学习算法与Python学习

一、介绍

目前，对于全球科学家而言，“如何去学习一种新技能”成为了一个最基本的研究问题。为什么要解决这个问题的初衷是显而易见的，如果我们理解了这个问题，那么我们可以使人类做一些我们以前可能没有想到的事。或者，我们可以训练去做更多的“人类”工作，常遭一个真正的人工智能时代。

虽然，对于上述问题，我们目前还没有一个完整的答案去解释，但是有一些事情是可以理解的。先不考虑技能的学习，我们首先需要与环境进行交互。无论我们是学习驾驶汽车还是婴儿学习走路，学习都是基于和环境的相互交互。从互动中学习是所有智力发展和学习理论的基础概念。

二、强化学习

今天，我们将探讨强化学习，这是一种基于环境相互交互的学习算法。有些人认为，强化学习是实现强人工智能的真正希望。这种说法也是正确的，因为强化学习所拥有的潜力确实是巨大的。

目前，有关强化学习的研究正在快速增长，人们为不同的应用程序生成各种各样的学习算法。因此，熟悉强化学习的技术就变得尤其重要了。如果你还不是很熟悉强化学习，那么我建议你可以去看看我以前有关强化学习文章和一些开源的强化学习平台。

一旦你已经掌握和理解了强化学习的基础知识，那么请继续阅读这篇文章。读完本文之后，你会对强化学习有一个透彻的了解，并且会进行实际代码实现。

注：在代码实现部分，我们假设你已经有了Python的基本知识。如果你还不知道Python，那么你应该先看看这篇教程。

1. 确定一个强化学习问题

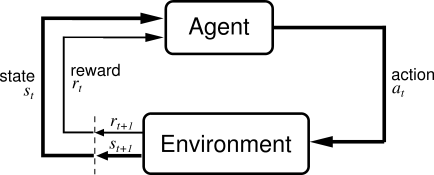
强化学习是学习如何去做，如何根据与环境的交互采取相应的行动。最终的结果就是使得系统的回报信号数值最大化。学习者不会被告知去执行哪个行动，而是要他自己去发现哪种行动将产生最大的回报。让我们通过一个简单的例子来解释一下：

我们将一个正在学习走路的孩子作为一个例子。

以下是孩子在学习走路时所要采取的步骤：

1.孩子会观察的第一件事，就是注意你是如何走路的。你使用两条腿，一次走一步，一步一步往前走。孩子会抓住这个概念，然后试图去模仿你。

2.但很快他/她又会明白，在走路之前，孩子必须先站起来！在学习走路的时候，这对于孩子来说是一个挑战。因此，孩子试图自己站起来，他/她不断跌倒，但是任然不断地站起来。

3.然而还有另外一个挑战需要应付。站起来是相对容易的，但是要保持站立状态就是另一个挑战了。在一个狭小的空气中，找到支撑，孩子设法保持站立。

4.现在，孩子的真正任务就是开始学习走路了。但是学习走路说起来很容易，而实际做起来就不是那么容易了。在孩子的大脑中需要处理很多事情，比如平衡身体，决定哪个脚是下一次需要放下的，放在哪里。

这听起来像是一个很困难的任务，对吗？它实际上确实是一个挑战，先要学习站立，然后才能学习行走。但是，现在我们不都学会了走路嘛，再也不会被这个问题所困扰了。现在，你可以明白，为什么这对于孩子是多么困难的原因了。

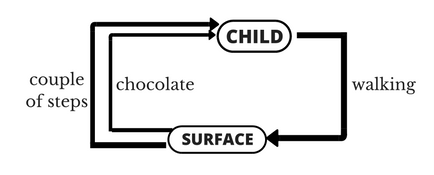
让我们形式化上面的例子。例子所要陈述的问题是“走路问题”，其中孩子是一个试图通过采取行动（走路）来操纵环境（在地上走路）的智能体，他/她试图从一个状态（即，他/她走的每一步）转移到另一个状态。当他/她完成任务的一个子模块（即，孩子走了几步）时，孩子会获得奖励（比如，一些巧克力），但是当他/她不会走路时，他/她不会收到任何巧克力（这是一个负反馈过程）。这就是像话学习问题的简单描述。

这是一个有关强化学习很好的介绍视频。

2. 与其他机器学习方法的比较

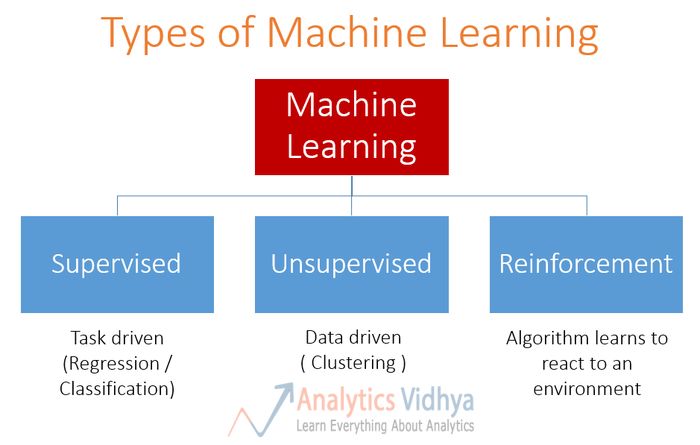
强化学习属于更打雷的机器学习算法。以下是有关机器学习算法类型的描述。

让我们比较一下强化学习算法和别的类型算法之间的区别：

监督学习与强化学习：在监督学习中，在外部有一个“监督主管”，它拥有所有环境的知识，并且与智能体一起共享这个知识，从而帮助智能体完成任务。但是这样存在一些问题，因为在一个任务中，其中存在如此多的子任务之间的组合，智能体应该执行并且实现目标。所以，创建一个“监督主管”几乎是不切实际的。例如，在象棋游戏中，存在数万个可以移动的玩法。因此，去创建一个可以获胜的玩法知识库是一个单调乏味的任务。在这些问题中，从自己的经验中学习，并且获得知识是更加合理可行的。这就是强化学习和监督学习的主要区别。在监督学习和强化学习中，在输入和输出之间都存在映射。但是在强化学习中，存在的是对智能体的奖励反馈函数，而不是像监督学习直接告诉智能体最终的答案。
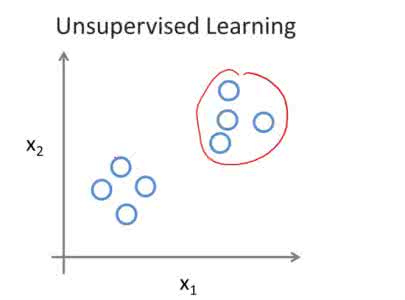
无监督学习与强化学习：在强化学习中，有一个从输入到输出的映射过程，但是这个过程在无监督学习中是不存在的。在无监督学习中，主要任务是找到一个最基础的模式，而不是一种映射关系。例如，如果任务是向用户推荐新闻文章，则无监督学习算法是先查看该人以前读过的类似文章，并把它们推荐给其他人。而强化学习算法则是，通过用户的一些文章，并且获得用户的不断反馈，从而构建一个“知识图谱”，从而得知用户与文章之间的喜爱关系。

还有第四种类型的机器学习，成为半监督学习，其本质上是监督学习和无监督学习的组合。它不同于强化学习，类似于监督学习和半监督学习具有直接的参照答案，而强化学习不具有。

3.解决强化学习问题的框架

为了理解如何去解决一个强化学习问题，让我们通过一个经典的例子来说明一下强化学习问题——多臂赌博机。首先，我们需要了解探索与开发的基本问题，然后去定义解决强化学习问题的框架。

Tiger Machine如上图，假设你已经在Tiger Machine上面玩了很多次了。

现在你想做的是从Tiger Machine上面获得最大的回报，并且尽可能的快。你会怎么做呢？

一个比较天真的想法是，只选择一个Tiger Machine，然后一整天都在玩它。这听起来非常无聊，但Tiger Machine可能会给你一些“报酬”，即让你赢钱。使用这种方法，你可能中奖的概率大约是0.00000.....1。也就是说，大多数时间你可能知识坐在Tiger Machine面前亏钱。正式说明一下，这可以被定义为一种纯粹的开发方法。但是这是最佳选择吗？答案当然是否定的。

让我们看看另外一种方法。我们可以拉每个Tiger Machine的拉杆，并且向上帝祈祷，让我们至少打中一个。当然，这是另一种天真的想法，你只会一天都在拉动拉杆，但只是给你一点点报酬。正式说明一下，这种方法只是一种纯粹的探索方法。

这两种方法都不是最优的，我们必须在它们之间找到适当的平衡点，已获得最大的回报。这被称为强化学习的探索和开发困境。

首先，我们正式的定义解决强化学习问题的框架，然后列出可能的方法来解决这个问题。

马尔科夫决策过程：

在强化学习场景中，我们定义问题的数学框架被称之为马尔科夫决策过程。这可以被设计为：

状态集合：S
动作集合：A
奖励函数：R
策略：π
价值：V

我们必须采取一定的行动（A），让我们从开始状态移动到结束状态（S）。每当我们采取一个行动之后，我们都会得到一定的回报作为奖励。当然，所获得的奖励的性质（正面奖励还是负面奖励）是由我们的行动决定的。

我们的策略集合（π）是由我们的动作集合来确定的，而我们得到的回报确定了我们的价值（V）。在这里，我们的任务就是通过选择正确的策略来最大化我们的价值。所以我们必须最大化下面的方程：

对于时间t，所有可能的S。

旅行推销员问题

让我们通过另外一个例子来说明一下。

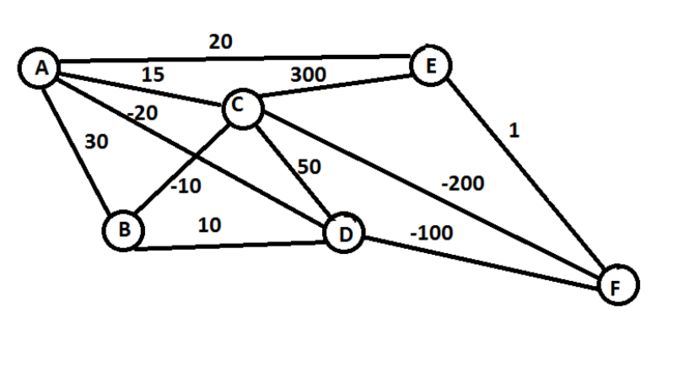
这个问题是一系列旅行商（TSP）问题的代表。任务是以尽可能低的成本，完成从地点A到地点F。两个字母之间的每条边上的数字表示两地之间的距离花费。如果这个值是负数，那么表示经过这条路，你会得到一定的报酬。我们定义价值是当你用选择的策略走完整个路程时，所获得的总价值。

这里说明一下符号：

状态节点集合：{A,B,C,D,E,F}
动作集合是从一个地点到另一个地点：{A->B, C->D, etc}
奖励函数是边上的值
策略函数指的是完整的路径规划，比如: {A -> C -> F}

现在假设你在地点A，唯一你能看见的路就是你下一个目的地（也就是说，你只能看见B，D，C，E），而别的地点你是不知道的。

你可以采取贪心算法，去获取当前状态下最有利的步骤，也就是说你从{A -> (B,C,D,E)}中选择采取 {A->D} 这种方法。同样，现在你所在的地点是D，想要到达地点F。你可以从{D -> (B, C, F)} 中采取 {D -> F} 这个方法，可以让你得到最大的报酬。因此，我们采取这一条路。

至此，我们的策略就是采取{A -> D -> F}，我们获得的回报是-120。

恭喜！你刚刚就实现了强化学习算法。这种算法被称之为 epsilon 贪婪算法。这是一种逐步测试从而解决问题的贪婪算法。现在，如果见你（推销员）想再次从地点A到地点F，你总是会选择这一条路了。

其他旅游方式？

你能猜出我们的策略是属于哪个类别（纯粹的探索还是纯粹的开发）吗？
请注意，我们采取的策略并不是一个最佳策略。我们必须“探索”一点，然后去寻找最佳的策略。在这里，我们采取的方法是局域策略的而学习，我们的任务是在所有可能的策略中找到最佳的策略。有很多的方法都可以解决这个问题，在这里，我们简要的列出一些主要类别：

策略优先：我们的重点是找到最佳的策略
回报优先：我们的重点是找到最佳的回报价值，即累计奖励
行动优先：我们的重点是在每个步骤上采取最佳行动

在以后的文章中，我会深入讨论强化学习算法。到那时，你可以参考这篇关于强化学习算法调研的论文。

4.强化学习的实现

接下来，我们将使用深度Q学习算法。Q学习是一种基于策略的学习算法，它具有和神经网络近似的函数表示。这个算法被Google使用，并且打败了Atari游戏。

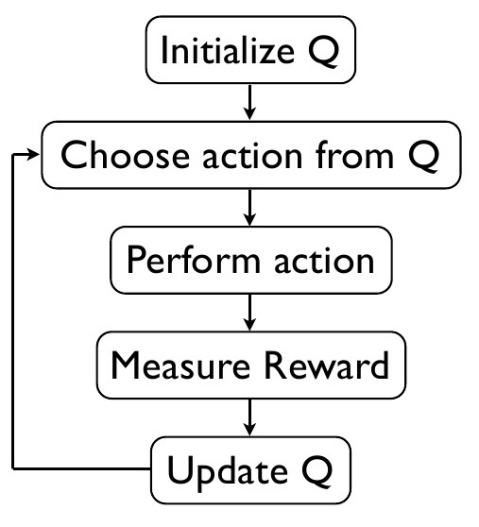
让我们看看Q学习的伪代码：

1.初始化价值表 ‘Q(s, a)’.
2.观察当前的状态值 ‘s’.
3.基于动作选择一个策略（例如，epsilon贪婪）作为该状态选择的动作.
4.根据这个动作，观察回报价值 ’r’ 和下一个新的状态 s.
5.使用观察到的奖励和可能的下一个状态所获得的最大奖励来更新状态的值。根据上述公式和参数进行更新。
6.将状态设置为新的状态，并且重复上述过程，直到达到最终状态。

Q学习的简单描述可以总结如下：

我们首先来了解一下 Cartpole 问题，然后继续编写我们的解决方案。

当我还是一个孩子的时候，我记得我会选择一根木棍，并试图用一只手指去使它保持平衡。我和我的朋友过去有这样一个比赛，看谁能让木棍保持平衡的时间更多，谁就能得到一块巧克力作为奖励。

这里有一个简单的视频来描述一个真正的 Cart-Pole 系统。

让我们开始编写代码吧！

在开始编写之前，我们需要先安装几个软件。

步骤一：安装 keras-rl包

在终端中，你可以运行以下命令：

git clone https://github.com/matthiasplappert/keras-rl.gitcd keras-rl python setup.py install

步骤二：安装CartPole环境的依赖

我们假设你已经安装好了pip，那么你只需要使用以下命令进行安装：

pip install h5py
pip install gym

步骤三：开始编写代码

首先我们需要导入一些我们需要的模块

import numpy as np import gym from keras.models import Sequential from keras.layers import Dense, Activation, Flatten from keras.optimizers import Adam from rl.agents.dqn import DQNAgent from rl.policy import EpsGreedyQPolicy from rl.memory import SequentialMemory

然后，设置相关变量

ENV_NAME = 'CartPole-v0' # Get the environment and extract the number of actions available in the Cartpole problem env = gym.make(ENV_NAME) np.random.seed(123) env.seed(123) nb_actions = env.action_space.n

之后，我们来构建一个非常简单的单层神经网络模型。

model = Sequential() model.add(Flatten(input_shape=(1,) + env.observation_space.shape)) model.add(Dense(16)) model.add(Activation('relu')) model.add(Dense(nb_actions)) model.add(Activation('linear')) print(model.summary())

接下来，我们配置和编译我们的智能体。我们将策略设置为 Epsilon 贪婪，我们还将我们的存储空间设置为序列存储，因为我们要需要存储我们执行操作的结果和每一个操作所获得的奖励。

policy = EpsGreedyQPolicy() memory = SequentialMemory(limit=50000, window_length=1) dqn = DQNAgent(model=model, nb_actions=nb_actions, memory=memory, nb_steps_warmup=10, target_model_update=1e-2, policy=policy) dqn.compile(Adam(lr=1e-3), metrics=['mae']) # Okay, now it's time to learn something! We visualize the training here for show, but this slows down training quite a lot. dqn.fit(env, nb_steps=5000, visualize=True, verbose=2)

现在，让我们来测试一下我们的强化学习模型

dqn.test(env, nb_episodes=5, visualize=True)

下图是模型的输出结果：

瞧，你刚刚就建立了一个强化学习机器人！

5.增加复杂性

现在，你已经看到了强化学习的一个基本实现，让我们开始学习更多的问题吧，每次增加一点点复杂性。

汉诺塔问题

对于那些不知道比赛的人来说，汉诺塔问题是在1883年发明的。它是由3根木棍和一系列大小不一的圆盘组成的（比如，上图中的3个）。从最左侧的木棍开始，目的是以最少的移动次数，把最左边的圆盘移动到最右边的圆盘上。

如果我们要处理这个问题，那么我们先从处理状态开始：

初始状态：三个圆盘都在最左边的木棍上（从上到下，依次编号为1,2,3）
结束状态：三个圆盘都在最右边的木棍上（从上到下，依次编号为1,2,3）

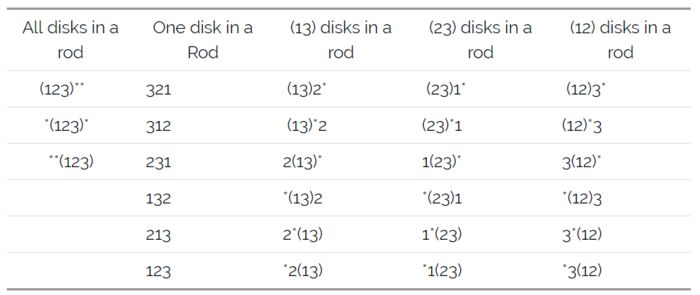
所有可能的状态：

这里是我们可能得到的27种状态：

其中，(12)3* 表示，圆盘1和圆盘2在最左边的木棍上面（从上往下编号），圆盘3在中间那个木棍上面，最右边的木棍没有圆盘。

数值奖励：

由于我们想要以最少的移动步数解决这个问题，所以我们可以给每个移动赋予 -1 的奖励。

策略：

现在，如果我们不考虑任何的技术细节，那么前一个状态可能会存在几种下一个状态。比如，当数值奖励为-1时，状态 (123)** 会转移到状态 (23)1，或者状态 (23)1 。
如果你现在看到了一个并发进行的状态，那么上面提到的这27个状态的每一个都可以表示成一个类似于旅行商问题的图，我们可以通过通过实验各种状态和路径来找到最优的解决方案。

3 x 3 魔方问题

虽然我可以为你解决这个问题，但是我想让你自己去解决这个问题。你可以按照我上述同样的思路，你应该就可以解决了。

从定义开始状态和结束状态开始，接下来，定义所有可能的状态及其转换，以及奖励和策略。最后，你应该就可以使用相同的方法来构建自己的解决方案了。

6.深入了解强化学习的最新进展

正如你所认识到的，一个魔方的复杂性比汉诺塔问题要高很多倍。现在，让我们来想象一下棋类游戏中的状态和选择的策略数量吧，比如围棋。最近，Google DeepMind公司创建了一个深度强化学习算法，并且打败了李世石。

最近，随着在深度学习方面的成功。现在的重点是在慢慢转向应用深度学习来解决强化学习问题。最近洪水一般的消息就是，由Google DeepMind创建的深度强化学习算法打败了李世石。在视频游戏中也出现了类似的情况，开发的深度强化学习算法实现了人类的准确性，并且在某些游戏上，超越了人类。研究和实践仍然需要一同前进，工业界和学术界共同策划努力，以实现建立更好地自适应学习机器人。