【夯实基础】卡尔曼滤波

会员服务 ·

【夯实基础】卡尔曼滤波

2021 年 11 月 3 日 极市平台

↑ 点击蓝字关注极市平台

作者 | Ai

来源丨宅码

编辑丨极市平台

极市导读

前段时间，我参加Kaggle谷歌手机定位赛，第一次了解到卡尔曼滤波。本文基于知乎问答：如何通俗并尽可能详细地解释卡尔曼滤波？[1]和MathWorks的系列视频《Understanding Kalman Filters》[2]，整理了卡尔曼滤波的内容。不足之处，还望批评指正。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

一、背景

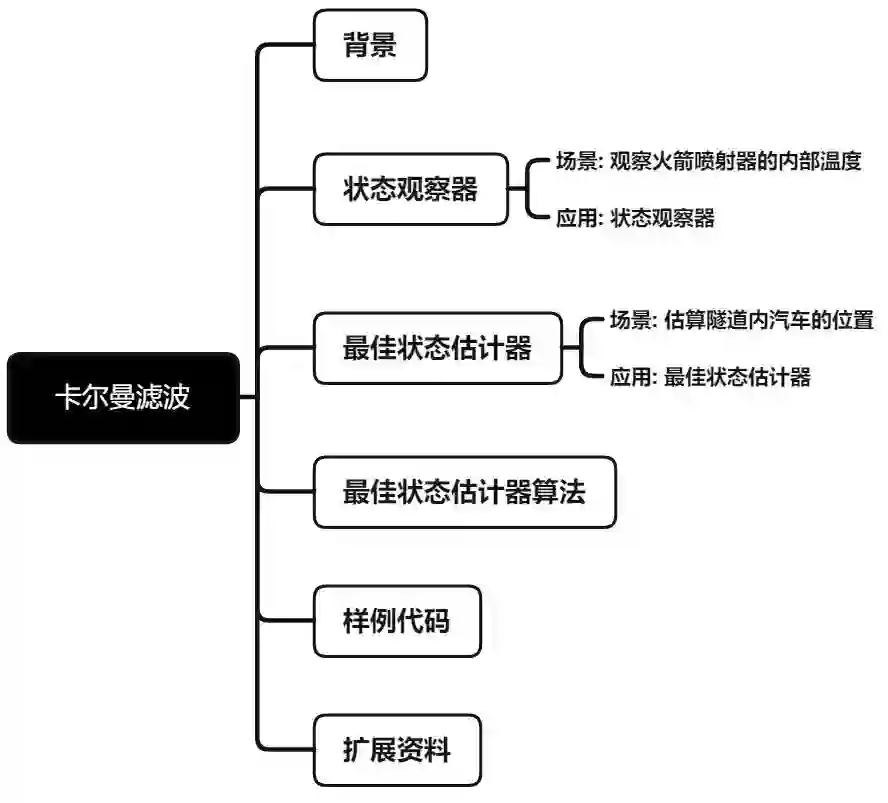
卡尔曼滤波(Kalman Filter，KF)是一种优化估算算法(Optimal Estimation Algorithm)，常用于制导与导航控制系统、计算机视觉系统和信号处理领域。实际作用主要是：从受误差影响的传感器测量中估算出最佳的系统状态。

在正式了解KF之前，我们先了解下状态观察器。

二、状态观察器

状态观察器(State Observers)：用于优化估算一些无法直接测量但可以间接测量的状态。

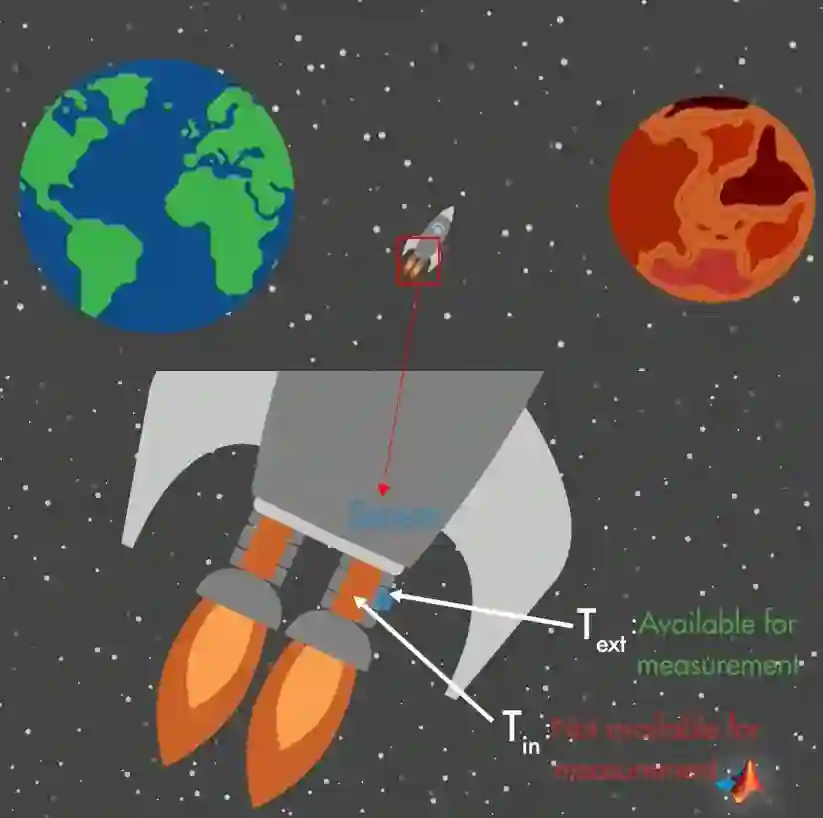
1.场景：观察火箭喷射器的内部温度

现在有一只火箭要从地球飞往火星，火箭使用液态氢作为燃料，但过高温度会导致火箭喷射器的机械部件损坏，因此监控喷射器内部温度就十分重要，可传感器不支持放置在喷射器内部，否则会被融化掉。但我们可以在喷射器外部的放置温度传感器，间接测量内部温度，但间接测量值和真实值存在误差，为此，我们可以使用状态观察器去基于间接测量值估算出真实值。

2.应用：状态观察器

状态观察器怎么“观察”出火箭喷射器的内部温度状态呢？

已知我们火箭燃料流量是，测量的外部温度是，假设我们有个数学模型可以基于估算出外部温度，那么，我们只要将估计的外部温度与测量的外部温度相匹配上，数学模型就会收敛到真实系统的模型，相应地，数据模型估算的内部温度也能逼近真实的内部温度。

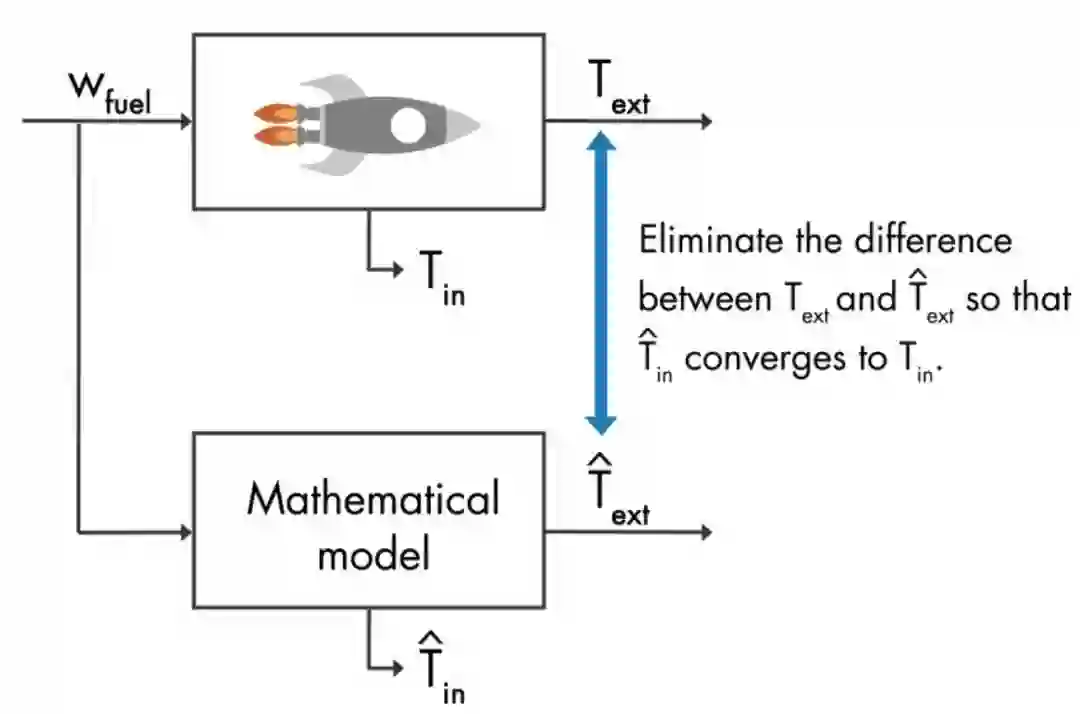
我们可以通过如图3的控制器K，控制测量和估计的外部温度之间的误差为0。

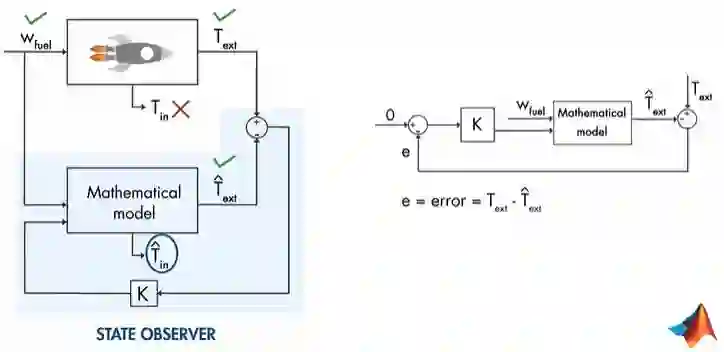
现在，我们透过数据公式来解释下状态观察器，如图4。为了方便理解公式，我先解释下变量：

：控制向量。这里是燃料流量，它控制了温度。
控制矩阵。
和矩阵和。
内部温度对时间的导数。
和：测量的内部温度和外部温度。
加了\wedge的变量都是预测的变量。

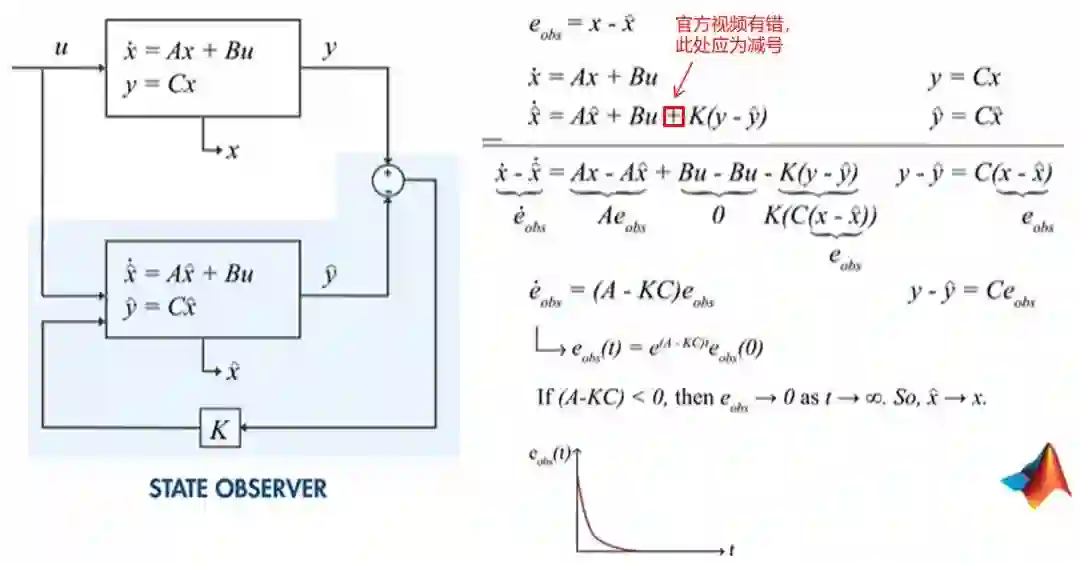
由于官方视频直接带过了的求解过程，这里我进行补充下，由于是内部温度误差对时间的导数，所以如果我们要获取内部温度误差随时间变化的函数，我们只要微分就好了，公式拆解如下:

结合视频说是个指数函数，因此我们可以联想到：

现在我们再对求导，可得到图 4 的结果：。我们现在知道是一个指数函数，是控制指数函数衰减的系数，但我们不能没有项，因为在状态观察器中，核心的控制变量是，由来调控误差函数的衰减速度。

三、最佳状态估计器

最佳状态估计器(Optimal State Estimator)：从受误差影响的传感器测量中估算出最佳的系统状态。

卡尔曼滤波本身便是一个最佳状态估计器，它跟前面讲的状态观察器差不多，不同的是KF是为随机系统设计的。区别如下：

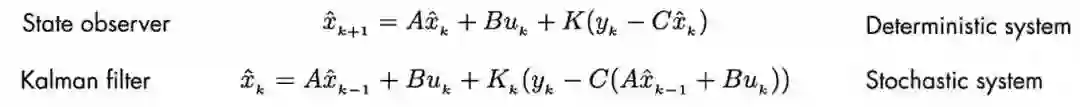
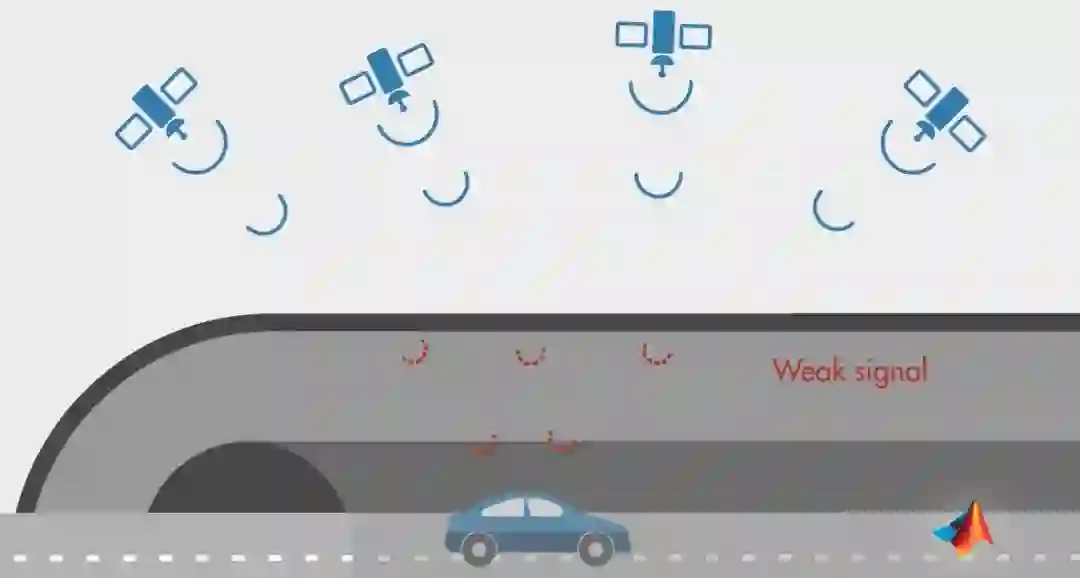
1.场景：估算隧道内汽车的位置

如果汽车进入隧道，汽车上的GPS接收器很难接收到卫星信号。如果在周围有高建筑物遮挡的街道上行驶，因为多路径效应(Multipath Effect，即信号失真)，导致定位噪声很大。我们可以简单看作这是一个传感器测量受误差影响的案例，如果我们想估算出汽车真实的位置状态，建议使用卡尔曼滤波。

2.应用：最佳状态估计器

接下来，我们来看下最佳状态估计器是如何估算汽车下一时间点会定位在哪的。

如图7所示，KF的目标是将GPS测量值(Measurement)和数学模型预测值(Prediction)相结合去找到汽车位置的最优估计状态(即汽车位置)。

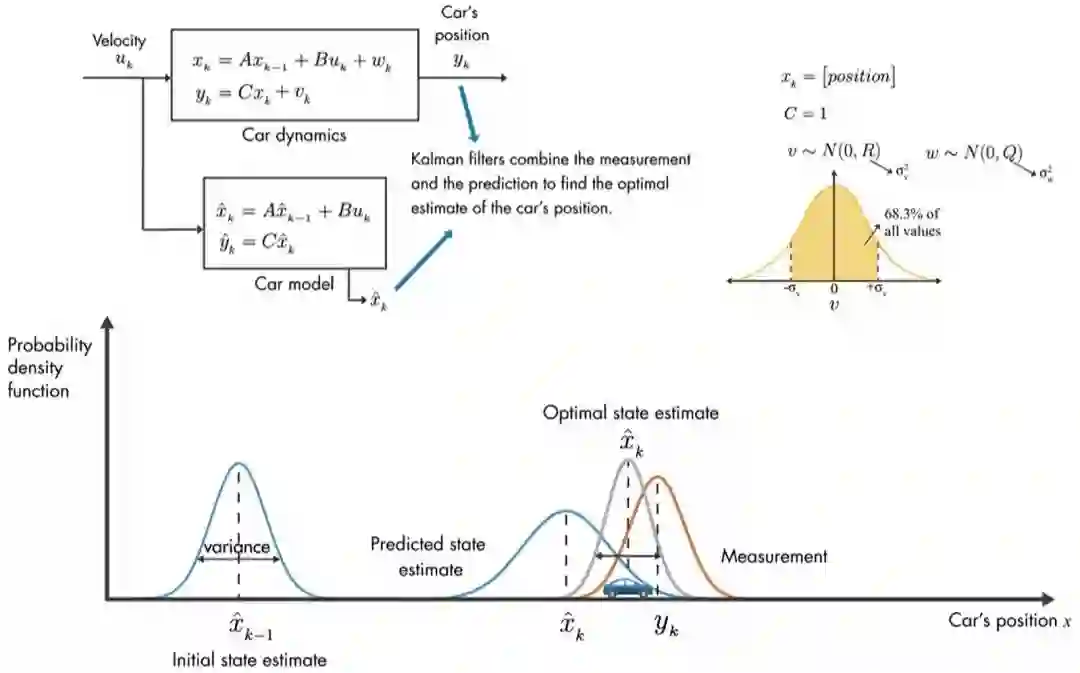
同样地，我先解释下图7中的变量：

时刻下的控制向量。这里是速度。
和：测量的位置和真正的位置。
过程噪声，随机变量，可以代表风的影响或汽车速度的变化。服从正态分布为协方差。
测量误差，随机变量，服从正态分布为测量值的协方差，由于我们这里是单输出系统，协方差R等同于测量误差的方差。
和矩阵变量。
加了\wedge的变量都是预测的变量。

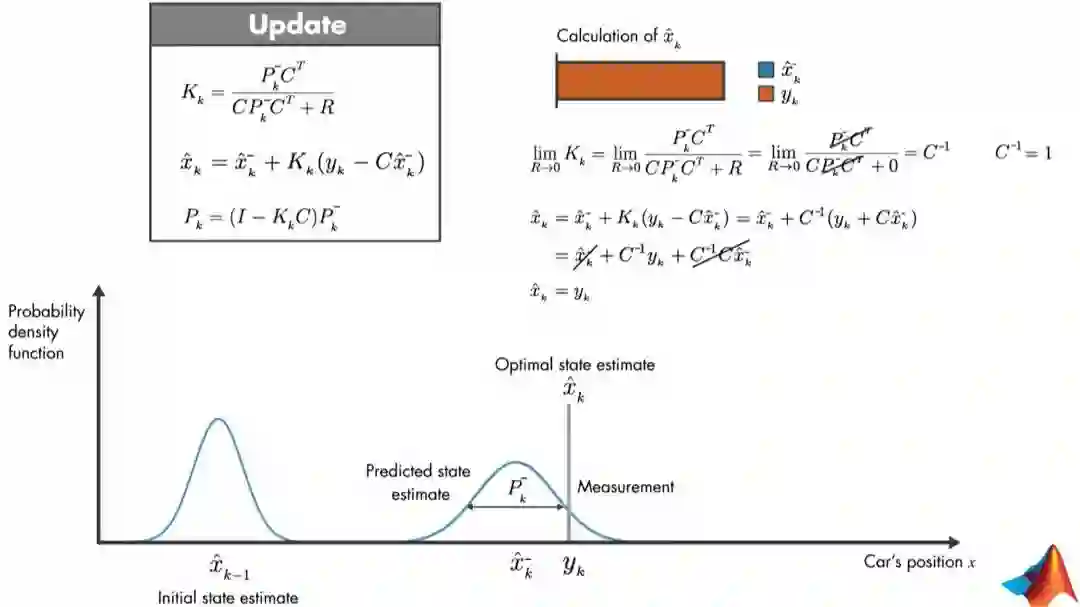
在图7中，我们用了概率密度函数去描述KF的中心思想，假设我们用数据模型得到时间点下汽车状态，由于是预估值，所以会存在一定的方差，现在我们使用汽车数学模型再次预测时间下的位置，由于误差累积，会有更大方差，同时我们也可以获取到测量值。现在我们有了预测和测量，我们便可以通过概率密度函数相乘的方式得到最优状态估计函数，而新的概率密度函数的平均值便是最优状态估计值(即我们综合测量值和预测值得到的最佳定位点)。

四、最佳状态估计器算法

现在，我们来详细看下KF是如何实现最佳状态估计器算法。如图8所示，我先解释下各变量:

：先验状态，即预测值。
后验状态，即最佳状态估计值。
先验协方差，即预测值的协方差。
后验协方差，即最佳状态估计值的协方差。
测量值噪声的协方差。
过程噪声的协方差。
：卡尔曼增益。
和矩阵。

KF步骤如下:

初始化和。
先执行Prediction，得到和。
将Prediction结果输入到Update模块，求得，再基于求最佳估计值。
将Update求出的和再输入给Prediction 。重复以上步骤，不断调整卡尔曼增益，使更新后的状态值误差协方差最小。

最后，我们深入看下卡尔曼增益K是怎么权衡测量值和预测值的决策比重？

1.当K=1/C时，测量值=最佳状态估计值

若测量值=最佳状态估计值，说明测量值协方差R趋向于0，那么如图9所示。

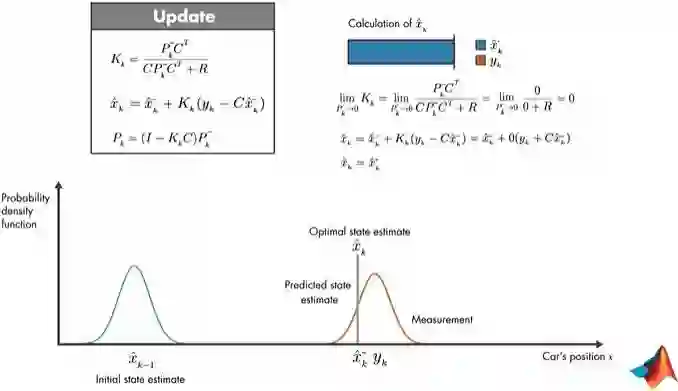
2.当K=0时，预测值=最佳状态估计值

若预测值=最佳状态估计值，说明预测值协方差趋向于0，那么如图10所示。

五、样例代码

simdkalman库[3]支持卡尔曼滤波，以下是参考[4]，给出的样例代码：

import numpy.random as random
import simdkalman
import numpy as np
import matplotlib.pyplot as plt

def make_shifted_matrix(vec):
    '''Define shifted matrix'''
    matrix = []
    size = len(vec)
    for i in range(size):
        row = [0] * i + vec[:size-i]
        matrix.append(row)
    return np.array(matrix)

def make_state_vector(T, size):
    '''Define state vector'''
    vector = [1, 0]
    step = 2
    for i in range(size - 2):
        if i % 2 == 0:
            vector.append(T)
            T *= T / step
            step += 1
        else:
            vector.append(0)
    return vector

def make_noise_vector(noise, size):
    '''Define noise vector'''
    noise_vector = []
    for i in range(size):
        if i > 0 and i % 2 == 0:
            noise *= 0.5
        noise_vector.append(noise)
    return noise_vector

# KF的参数，可用optuna去做搜索
T = 1
size = 4
noise = 2.1714133956113952e-06
obs_noise = 1.719317114286542e-05

# 获取State transition matrix A
vec = make_state_vector(T, size)
state_transition = make_shifted_matrix(vec)

# 获取Process noise (state transition covariance) matrix Q
process_noise = np.diag(make_noise_vector(noise, size)) + np.ones(size) * 1e-9

# 获取Observation model (measurement model) matrix C
observation_model = np.array([[1] + [0] * (size - 1)])

# 获取Observation noise (measurement noise covariance) matrix R
observation_noise = np.diag([obs_noise] * 1) + np.ones(1) * 1e-9

kf = simdkalman.KalmanFilter(
        state_transition = state_transition,
        process_noise = process_noise,
        observation_model = observation_model,
        observation_noise = observation_noise)

# 随机化一组样例数据
x = np.linspace(0, 10, 100)
y = np.sin(x)
data = np.array([v + random.normal(0.1, 0.3, 1) for v in y])
data = data.reshape(1, len(data), 1)

smoothed = kf.smooth(data)
smoothed_data = smoothed.states.mean[0, :, 0]

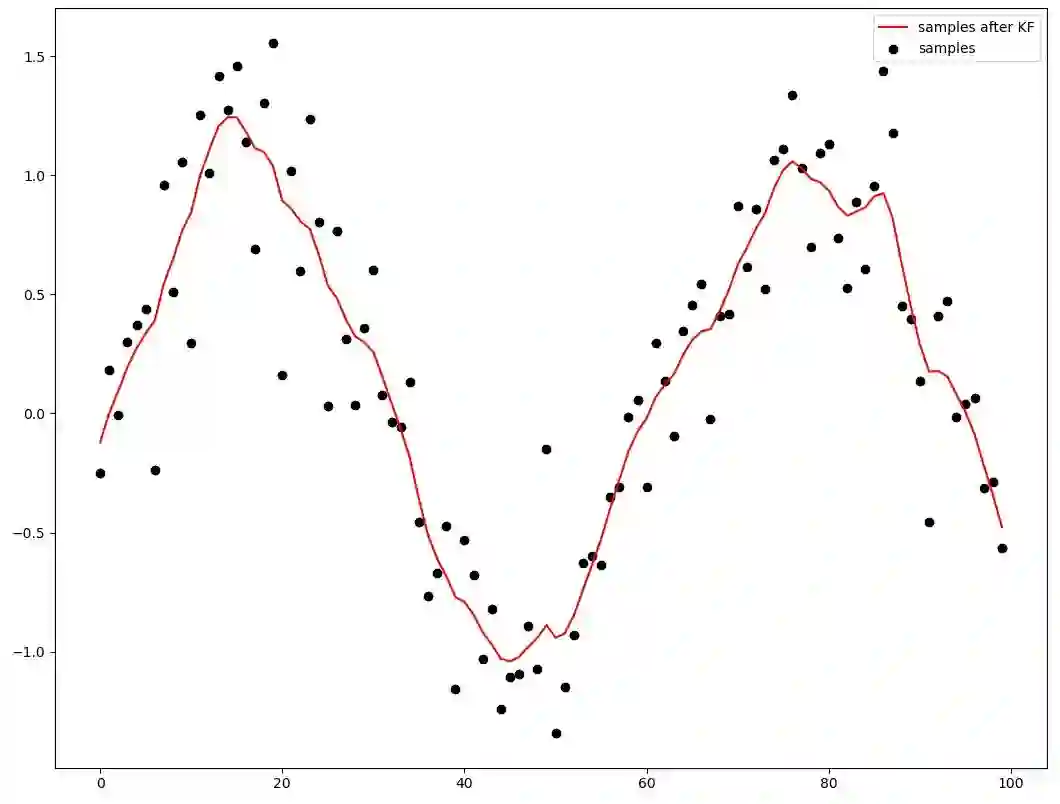
# 可视化
fig = plt.figure()
plt.scatter(range(len(data[0,:,0])), data[0,:,0], c = 'black', label = 'samples')
plt.plot(range(len(smoothed_data)), smoothed_data, c = 'r', label = 'samples after KF')
plt.legend()
plt.show()

六、扩展资料

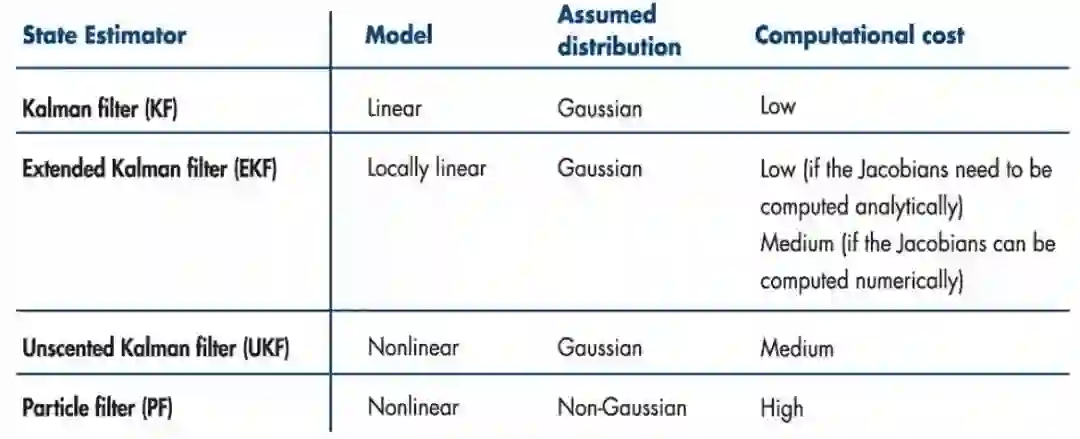
卡尔曼滤波是线性的，而实际中，很多数据模型是非线性的，此时可以考虑扩展卡尔曼滤波，另外，有兴趣的朋友也可以去了解无迹卡尔曼滤波和粒子滤波，如图12所示。

个人在查阅资料的时候，发现还有很多蛮深入的资料，适合深入了解卡尔曼滤波的数据原理，这里分享给有需要的朋友们：

1.MathWorks制作的《Understanding Kalman Filters》视频

英文视频：https://ww2.mathworks.cn/videos/series/understanding-kalman-filters.html。
翻译视频：https://www.zhihu.com/question/23971601，请参考知乎主：云羽落的回答。

2.Bzarg写的《How a Kalman filter works, in pictures》博文

英文博文：http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/#mathybits。
翻译博文：https://www.zhihu.com/question/23971601，请参考知乎主：米开朗基罗赵的回答。

3. Automatic Addison写的《Extended Kalman Filter (EKF) With Python Code Example》博文

英文博文：https://automaticaddison.com/extended-kalman-filter-ekf-with-python-code-example/。

参考资料

[1]《如何通俗并尽可能详细地解释卡尔曼滤波？》-知乎，问答：https://www.zhihu.com/question/23971601
[2]《Understanding Kalman Filters》- MathWorks，系列视频：https://ww2.mathworks.cn/videos/series/understanding-kalman-filters.html
[3]卡尔曼滤波库simdkalman，Github：https://github.com/oseiskar/simdkalman
[4]《Kalman filter - hyperparameter search with BO》-Trinh Quoc Anh，代码：https://www.kaggle.com/tqa236/kalman-filter-hyperparameter-search-with-bo

如果觉得有用，就请分享到朋友圈吧！

△点击卡片关注极市平台，获取最新CV干货

公众号后台回复“CVPR21检测”获取CVPR2021目标检测论文下载～