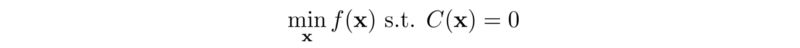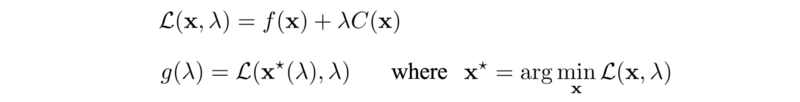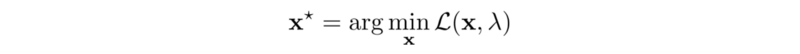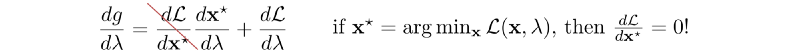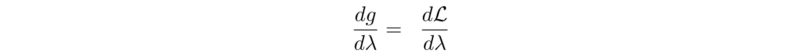强化学习基础-对偶梯度上升

本文为 AI 研习社编译的技术博客，原标题 ：

The base of deep reinforcement-learning-Dual Gradient Descent

作者 | Jonathan Hui

翻译 | 斯蒂芬•二狗子

校对 | 斯蒂芬•二狗子       审核| 莫青悠      整理 | 菠萝妹

原文链接：

https://medium.com/@jonathan_hui/rl-dual-gradient-descent-fac524c1f049

注：本文的相关链接请点击文末【阅读原文】进行访问

强化学习基础-对偶梯度上升

对偶梯度下降是一个优化带约束目标函数的常用方法。在强化学习中，该方法可以帮助我们做出更好的决策。

该方法的核心思想是把目标函数转换为可以迭代优化拉格朗日对偶函数。其中拉格朗日函数 𝓛 和拉格朗日对偶函数 g 定义为：

其中标量 λ 被称为拉格朗日乘子。

对偶函数 g 是原始优化问题的下限，实际上，若 f 是凸函数，g和f保持强对偶关系，即g函数的最大值等价于优化问题的最小。只要找到使得g最大的 λ ，我们就解决了原始优化问题。

所以，我们随机指定 λ 为初始值，使用优化方法解决这个无约束的g(λ)。

接下来，我们将应用梯度上升来更新 λ 以便最大化g。 g的梯度是：

即为

在下面的步骤1中，我们根据当前的 λ 值找到最小x，然后我们对g进行梯度上升（步骤2和3）。

先最小化带有原始x变量的拉格朗日𝓛，再用梯度法更新拉格朗日乘子 λ ，不断交替着进行这两种计算。通过这样重复迭代，λ、x将收敛。

  可视化

让我们想象一下这个算法是如何工作的。

Modified from source

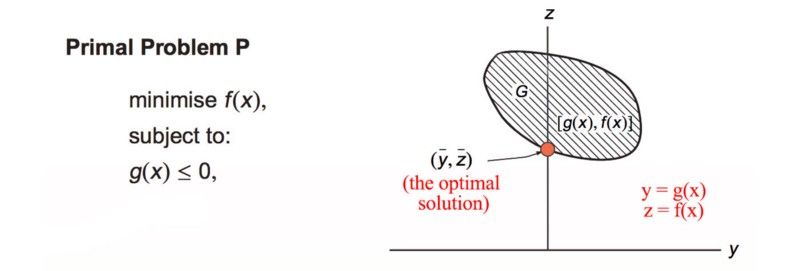
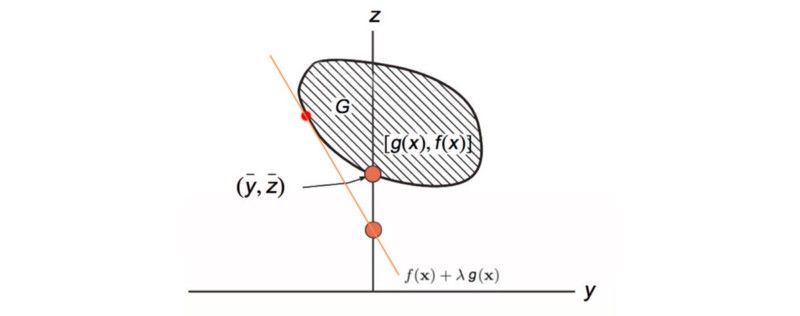
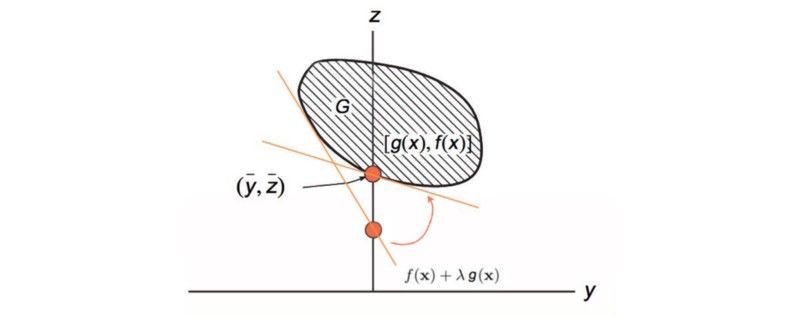
设 y = g(x)， z = f(x)。y 和 z 在来自于空间 G ，我们画出了与y对应的z。我们的解是上面的橙色的点： 空间 G上的最小f同时满足g(x)= 0。下面的橙色线是拉格朗日函数。它的斜率等于λ，它接触G的边界 。

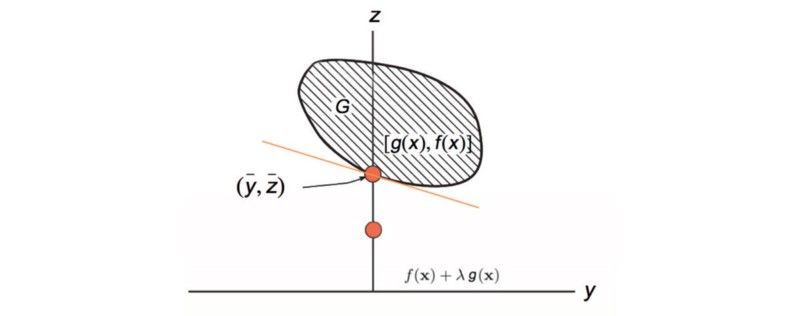
然后我们使用梯度上升来调整 λ（斜率），以获得与 g(x)= 0 接触G的最大值 f(x) 。

Modified from source

这就是对偶梯度上升法的工作原理。（PPT）

  示例

让我们通过一个示例来分析如何求解的。

  拉格朗日乘子

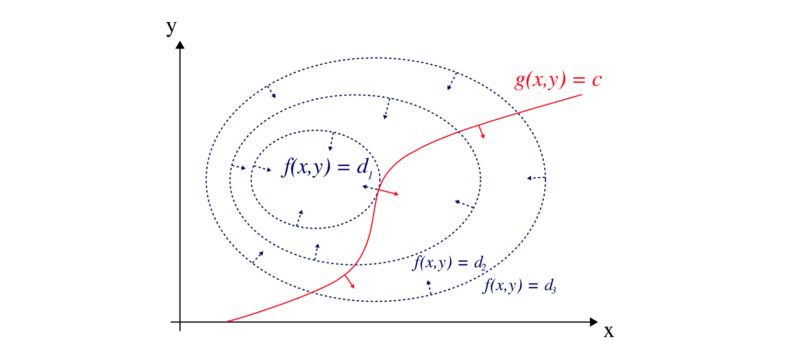
那么，拉格朗日乘子是什么？我们可以使用不同d值的等高线图可视化f函数。g是约束函数。

其中 λ 是拉格朗日乘子

  思考

对偶梯度下降可以使用任何优化方法来最小化具有λ值的拉格朗日函数。在轨迹优化问题中，我们一般使用的优化方法为iLQR。然后我们应用梯度上升来调整λ。通过重复迭代可以找到最优解。

想要继续查看该篇文章相关链接和参考文献？

长按链接点击打开或点击底部【阅读原文】：

https://ai.yanxishe.com/page/TextTranslation/1427

AI研习社每日更新精彩内容，观看更多精彩内容：

盘点图像分类的窍门

动态编程：二项式序列

如何用Keras来构建LSTM模型，并且调参

一文教你如何用PyTorch构建 Faster RCNN

等你来译：

如何在神经NLP处理中引用语义结构 

你睡着了吗？不如起来给你的睡眠分个类吧！ 

高级DQNs：利用深度强化学习玩吃豆人游戏

深度强化学习新趋势：谷歌如何把好奇心引入强化学习智能体 

点击 阅读原文 查看本文更多内容↙