数据科学中的数学基础: 矩阵和向量空间 |《精通数据科学》

站在数据学科的角度, 融合数学、计算机科学、计量经济学的精髓.
If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is.
如果有人不相信数学是简单的,那是因为他们没有意识到人生有多复杂。
——John von Neumann
下文节选自《精通数据科学:从线性回归到深度学习》, 已获异步授权许可, [遇见数学] 特此表示感谢!
毫无疑问,数学是数据科学的灵魂。不管是机器学习或是统计学模型,从本质上讲都是数学模型,因此,扎实的数学知识对于理解模型假设和分析模型结果至关重要。可能很多读者会觉得“数学”这两个字就代表了枯燥和难以理解,事实也许有时如此,但正如“计算机之父”冯·诺依曼说的那样,我们并不理解数学,只是越来越习惯它。本章的目的也一样, 就是让读者熟悉数据科学中常遇到的数学概念和数学符号,在阅读本书后续章节或者参考其他文献时,不再害怕面对它们。本章将简单介绍 3 个方面的数学知识。
矩阵和向量空间:矩阵是数据的基本表示形式,本书后面的所有章节都会涉及这部分内容。
概率:概率作为量化随机性的工具,是统计学和贝叶斯框架的核心内容。第 4、5、7、9 章中会有大量的概率运算及推导。
微积分:它是计算机解决最优化问题(也就是求函数的最值)的理论基础,出现频率较高的章节为第 6、12、13 章。
3.1 矩阵和向量空间
在数据科学领域,数据和模型的存在形式都是矩阵,而后者则直观地表示为向量空间里的点。矩阵和向量空间这两个数学概念是本节讨论的内容。
3.1.1 标量、向量与矩阵
首先通过一个简单例子来感性认识一下标量(scalar)、向量(vector)和矩阵(matrix)这 3 个数学概念。
假设我们设计了一款网络对战游戏,在游戏中,玩家选择自己的英雄与其他玩家对战。每个英雄的能力由 3 种属性描述:智力、敏捷和力量。为了方便表示,不妨用 i 表示智力、a 表示敏捷、s 表示力量。
对于英雄 A,它的设定是智力型英雄,智力被设定为 10,敏捷为 6 以及力量为 2,用数学式子表示为 i = 10, a = 6, s = 2。换句话说,我们用数字表表示各个属性具体的值,这在数学上就叫作标量,标量其实就是数字。
将这 3 个属性按照智力、敏捷和力量的顺序写在一起,就可以表示一个英雄的能力了。
比如用A = (10, 6, 2)表示英雄 A。在数学上A被称为向量,正确地说应该是行向量。直观上, 行向量是多个数字(标量)排成一行。与之类似的是列向量,即多个数字排成一列。
现在我们设计了另外 3 个英雄,分别为 B、C 和 D,向量表示为B = (3, 4, 10)、C = (5, 10, 4)和D = (6, 9, 5)。将这 4 个英雄的向量排列成矩形阵列,即每一行表示一个英雄,得到图 3-1 所示的矩阵,而这个矩阵就可以表示所有 4 个英雄的属性数据。
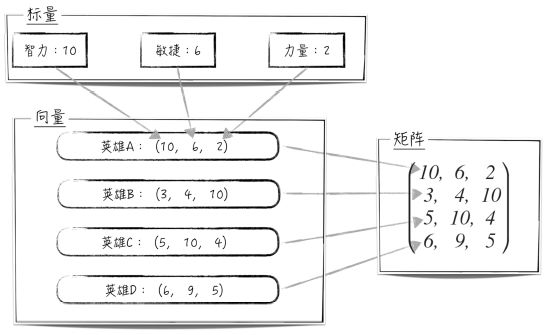
图3-1
用学术语言来定义矩阵:一个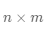
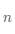
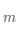
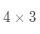
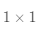
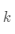
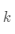
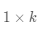
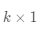
在数学上,通常如公式(3-1)所示表示向量和矩阵,其中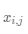
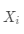
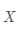
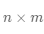
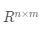
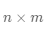
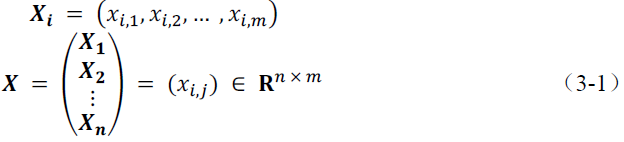
3.1.2 特殊矩阵
在讨论矩阵运算之前,先来看一类特殊的矩阵:方阵(squared matrix)。它是行数等于列数的矩阵。从形状上来看,它就像一个正方形,因此被称为方阵。有 3 种方阵需要特别注意。
• 单位矩阵(identity matrix),矩阵的对角线元素等于 1,其他元素等于 0,记为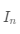
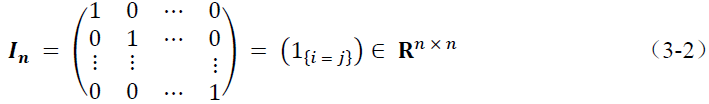

• 对角矩阵(diagonal matrix),除矩阵的对角线元素外,其他元素都等于 0,记为
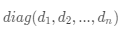 。不难注意到,单位矩阵是一种特殊的对角矩阵。
。不难注意到,单位矩阵是一种特殊的对角矩阵。
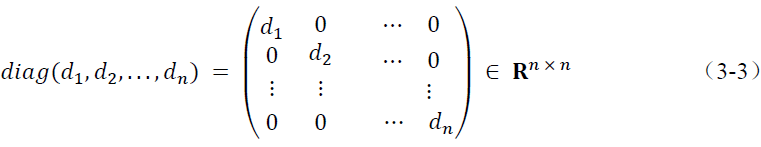
• 三角矩阵(triangular matrix),它可以细分为上三角矩阵和下三角矩阵两种。上三角矩阵的对角线下方的元素全部为零,记为
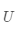 ;下三角矩阵的对角线上方的元素全部为零,记为
;下三角矩阵的对角线上方的元素全部为零,记为
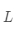 。不难发现,对角矩阵是一种特殊的三角矩阵。
。不难发现,对角矩阵是一种特殊的三角矩阵。

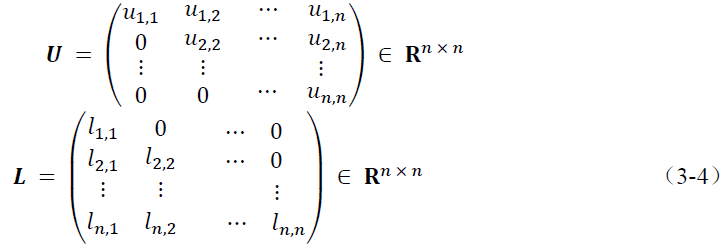
3.1.3 矩阵运算
为了能像使用数字一样使用矩阵,我们为它定义了“加减乘除”四种运算。
1.矩阵的加减法
(1)与数字的加减法不同,并不是任何两个矩阵都可以进行加减运算,要求矩阵的形状是一样的,也就是它们的行数和列数都相等。假设矩阵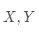
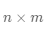
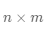
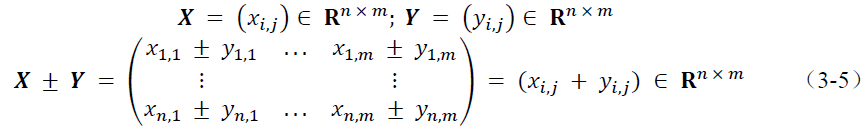

(2)根据上面的定义,不难得出,矩阵的加法也满足结合律和交换律。假设
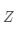 也是一个
也是一个
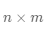 的矩阵,可以得到如下的公式 :
的矩阵,可以得到如下的公式 :
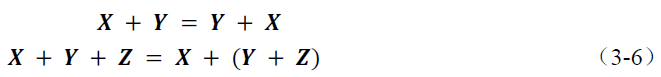

2.矩阵的乘法
(1) 矩阵与数字的乘法。与数字的乘法类似,任意一个实数都能和任意一个矩阵相乘。假设
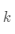 为实数,则它与矩阵
为实数,则它与矩阵
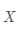 的乘法定义如下:
的乘法定义如下:
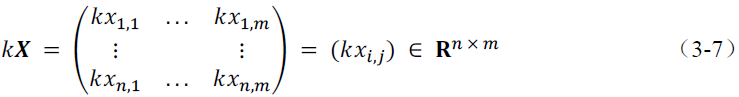

(2) 矩阵与矩阵的乘法。它只有在第一个矩阵的列数和第二个矩阵的行数相同时才有定义。假设
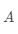 为
为
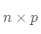 的矩阵,
的矩阵,
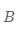 为
为
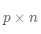 的矩阵,则它们之间的乘积为一个
的矩阵,则它们之间的乘积为一个
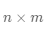 的矩阵,记为
的矩阵,记为
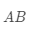 ,具体的定义如下:
,具体的定义如下:
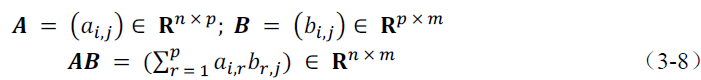

举个具体的例子:
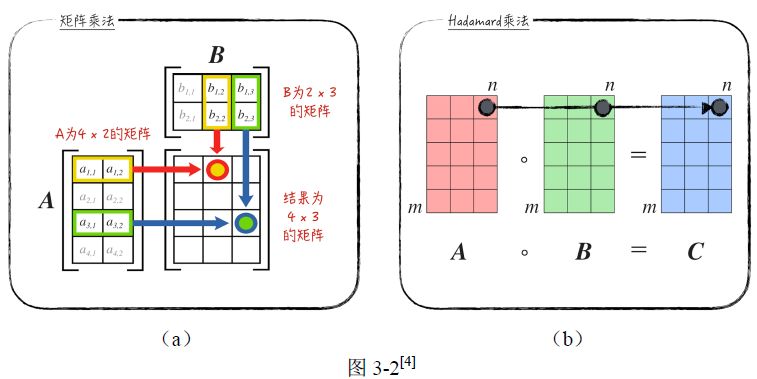
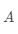 为4 × 2的矩阵,
为4 × 2的矩阵,
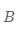 为2 × 3的矩阵,它们之间的乘法计算过程如图3-2a 所示。
为2 × 3的矩阵,它们之间的乘法计算过程如图3-2a 所示。

不难证明,矩阵的乘法满足结合律, 即
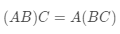 ,以及分配律, 即
,以及分配律, 即
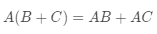 ,但不满足交换律(在通常情况下,两个矩阵交换顺序后,乘法运算的要求都不再满足)。这一点与数字的乘法有很大的不同。另外,任何一个矩阵与单位矩阵的乘积(前提条件是矩阵乘法的要求被满足)等于其本身,比如
,但不满足交换律(在通常情况下,两个矩阵交换顺序后,乘法运算的要求都不再满足)。这一点与数字的乘法有很大的不同。另外,任何一个矩阵与单位矩阵的乘积(前提条件是矩阵乘法的要求被满足)等于其本身,比如
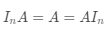 。因此单位矩阵可以被看作矩阵中的 1。
。因此单位矩阵可以被看作矩阵中的 1。
在实际中,线性模型常常用矩阵乘法来表示。举个简单的例子,假设线性模型为:


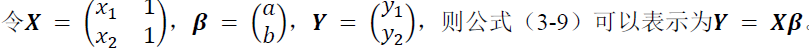

(3) 矩阵的 Hadamard 乘积(Hadamard product 或者element-wise multiplication)。假设矩阵
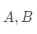 同为
同为
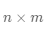 的矩阵,则它们之间的Hadamard 乘积仍为
的矩阵,则它们之间的Hadamard 乘积仍为
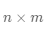 的矩阵,记为
的矩阵,记为
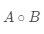 。
。
计算过程如图3-2b 所示,具体的公式如下:


矩阵的Hadamard 乘积在数学上并不太常用,但在编程时,我们常用它来同时计算多组数据的乘积。
3.矩阵的除法:逆矩阵(inverse matrix)
(1)对矩阵求逆是专门针对方阵的,即行数等于列数的矩阵。假设
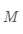 是一个
是一个
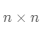 的矩阵,若存在一个
的矩阵,若存在一个
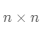 的矩阵
的矩阵
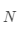 使得它们的乘积等于
使得它们的乘积等于
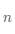 阶单位矩阵,如公式(3-11)所示,则称矩阵
阶单位矩阵,如公式(3-11)所示,则称矩阵
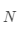 为矩阵
为矩阵
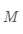 的逆矩阵,记为
的逆矩阵,记为
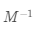 ,而
,而
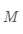 则被称为可逆矩阵。
则被称为可逆矩阵。


(2)数学上可以证明,一个矩阵的逆矩阵如果存在,则逆矩阵唯一。所以对于方阵
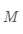 ,如果存在另一个方阵
,如果存在另一个方阵
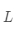 ,使得
,使得
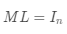 ,则一定有
,则一定有
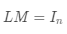 ,且
,且
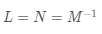 。
。
(3)关于逆矩阵,有如下几个常用的公式:


4.矩阵的转置(transpose)
(1)形象点理解,矩阵的转置就是将矩阵沿着对角线对调一下。假设
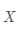 为
为
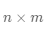 的矩阵,则它的转置为
的矩阵,则它的转置为
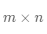 的矩阵,记为
的矩阵,记为
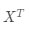 。具体的公式如下:
。具体的公式如下:


(2)关于矩阵的转置,有如下几个常用的公式,其中假设
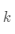 为实数,而且公式中涉及的矩阵乘法和逆矩阵都是有意义的。
为实数,而且公式中涉及的矩阵乘法和逆矩阵都是有意义的。



3.1.4 代码实现(略, 详见书描述)
3.1.5 向量空间
向量空间(vector space)是一个比较深刻的数学概念。为了便于理解,我们抛开复杂的公理化定义,从直观上来理解向量空间的相关知识。
我们生活的世界在空间上是一个三维空间,在这个现实世界里建立长宽高坐标系,也就是
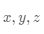 坐标系。这个现实中的每一个点都能被表示成一个三维行向量,如图3-3a 所示。
坐标系。这个现实中的每一个点都能被表示成一个三维行向量,如图3-3a 所示。
从数学上来看,任意一个三维的行向量
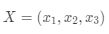 ,可以被写为
,可以被写为
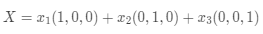 。用学术一些的话来表述就是任意一个三维行向量可以被
。用学术一些的话来表述就是任意一个三维行向量可以被
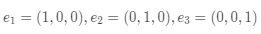 这3 个行向量线性表示,而且反过来,
这3 个行向量线性表示,而且反过来,
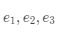 这3 个行向量的任意线性组合都对应着现实空间中的某一点。像这样的空间被称为向量空间,而
这3 个行向量的任意线性组合都对应着现实空间中的某一点。像这样的空间被称为向量空间,而
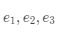 被称为向量空间的基。不难看出,其实
被称为向量空间的基。不难看出,其实
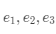 分别对应着
分别对应着
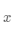 轴、
轴、
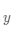 轴和
轴和
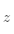 轴。
轴。
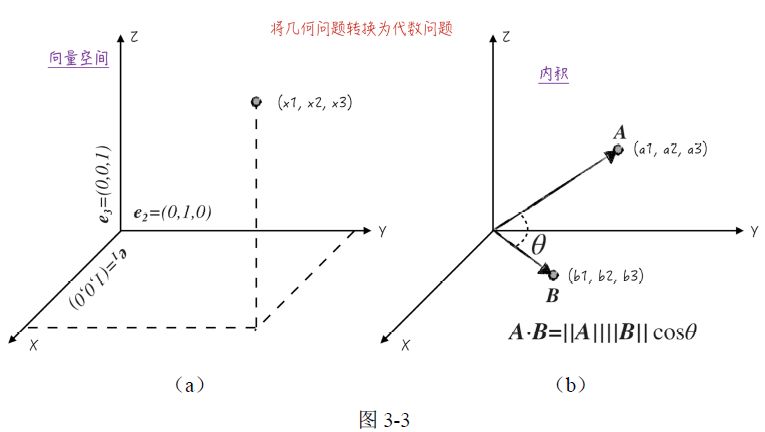

针对三维向量空间,定义行向量的内积(dot product)。假设行向量
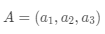 和行向量
和行向量
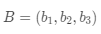 ,它们之间的内积定义为:
,它们之间的内积定义为:
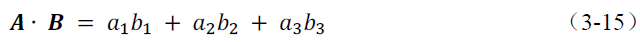
其实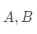
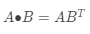
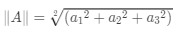
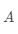
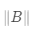
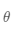
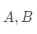
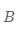
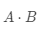
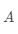


有了内积定义后,就可以更加数理化地定义向量间的正交关系(对应到空间上,就是两个向量相互垂直)。若两个行向量
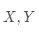 的内积等于0,则称它们是正交的。容易得到,上面提到的基
的内积等于0,则称它们是正交的。容易得到,上面提到的基
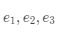 是相互正交的,被称为正交基。
是相互正交的,被称为正交基。
既然行向量可以被看作三维空间里的一个点,那么
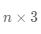 的矩阵
的矩阵
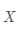 可以被看作三维空间里点的集合。现在我们想在这个空间里找到一条直线,使得矩阵中的点在这条直线的投影之和最长。结合内积的定义,假设
可以被看作三维空间里点的集合。现在我们想在这个空间里找到一条直线,使得矩阵中的点在这条直线的投影之和最长。结合内积的定义,假设
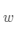 为行向量,将上面的目标表示为数学公式,其中向量
为行向量,将上面的目标表示为数学公式,其中向量
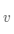 是长度为1 的向量,表示直线的方向。
是长度为1 的向量,表示直线的方向。
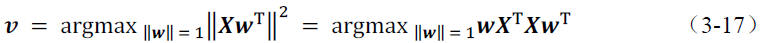

为了解决这个问题,需要引入另一个很复杂的数学概念:特征向量(eigenvector)和特征值(eigenvalue)。假设
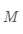 是一个三阶对称矩阵,即
是一个三阶对称矩阵,即
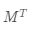 (注意到公式(3-17)里,
(注意到公式(3-17)里,
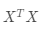 就是一个三阶对称矩阵)。满足下面条件的非零行向量
就是一个三阶对称矩阵)。满足下面条件的非零行向量
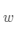 被称为
被称为
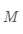 的特征向量,对应的
的特征向量,对应的
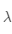 被称为特征值。
被称为特征值。


数学上可以证明,对于三阶的对称矩阵,存在3 个相互正交的特征向量,而它们可以组成三维空间的一组基。有了上面的结论,公式(3-17)定义的问题就很好解决了: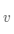
上面有关向量空间、内积、向量间夹脚以及正交的定义可以推广到任意维度的空间。有关特征向量、特征值的定义和结论也如此。(本节完)