基础｜什么是张量、数据立体、矩阵、向量和纯数

会员服务 ·

基础｜什么是张量、数据立体、矩阵、向量和纯数

2017 年 7 月 14 日 全球人工智能

欢迎加入全球最大AI社群>>

来源：云栖社区作者：码府

张量就是一个变化量。

张量有零阶、一阶、二阶、三阶、四阶等等。

零阶张量是纯量（数值）

一阶张量是向量（数值和方向的组合）

二阶张量是矩阵（向量的组合）

三阶张量是数据立体（矩阵的组合）

四阶张量（数据立体的组合）

等等。

1、纯量就是一个数值，可以看成是一个数值上的变化量。

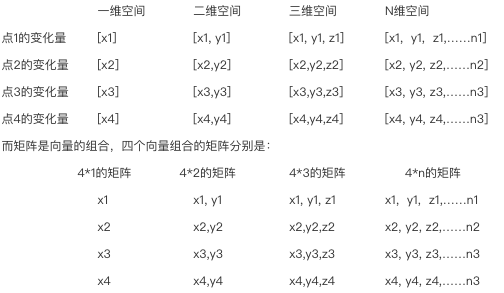
2、向量是点到点的变化量，而点可以是一维空间上的点、二维空间上的点、三维空间上的点，等等。

一维空间上的点的变化，好像点(x)在线上的移动，也即是左右的线性变化，变化量可以表示为[x1]。

二维空间上的点的变化，好像点(x,y)在面上的移动，也即是前后左右的线性变化，变化量可以表示为[x1, y1]。

三维空间上的点的变化，好像点(x,y,z)在体上的移动，也即是前后上下左右的线性变化，变化量可以表示为[x1, y1, z1]。

N维空间上的点的变化，好像点(x,y,z,.....n)在体上的移动，也即是2n个方向的线性变化，变化量可以表示为[x1, y1, z1,……n1]。

3、矩阵是图形到图形的变化量，而图形可以是一维的线、二维的面、三维的体，等等。

3.1、一维的线的变化，我们知道两点可以表示一线段，则需要用两个向量组成的矩阵对两点进行变化，就能达到对线段的变化。

3.2、二维的面的变化，我们知道三点可以表示一个三角形，四点可以表示一个四边形，五点可以表示一个五边形，等等。就拿三角形来说，需要用三个向量组成的矩阵对三点进行变化，就能达到对三角形的变化。

3.3、三维的体的变化，我们知道4点可以表示一个三角堆，5点可以表示四棱锥、6点可以表示一个三棱柱，等等。就拿三角堆来说，需要用四个向量组成的矩阵来对四个顶点进行变化，就能达到对三角堆的变化。

4、三阶张量可以表示图像的变化量，图像与图形的不同是图像的点除了有坐标，还具有颜色特性，如RGB、RGBA、YCbcr等表示的颜色。拿RGB的图像来说，它的变化量包括坐标和色值变化。图像坐标的变化相当于图形的变化，即是一个矩阵的变化。色值变化也就是RGB在颜色空间中的一个点变化，也是一个矩阵的变化，图像变化有两个矩阵变化，三阶张量是矩阵的组合，则可以用三阶张量来表示图像的变化量，如tensor[3,5,5]表示3颜色通道的5*5大小图形的变化量。

5、四阶张量在TensorFlow的神经卷积网络中，经常用到。下面举个例子。

5.1、输入张量格式：[batch, in_height, in_width, in_channels]

5.2、卷积核格式：[filter_height, filter_width, in_channels, out_channels]

5.3、我们来对输入图片进行卷积得到特征图片。

一张5通道的5*5的输入图片：input = [1, 5, 5, 5];

5输入通道、7输出通道的3*3大小的卷积核：filter = [3, 3, 5, 7];

strides=[1,1,1,1]表示各个方向步长为1；

padding=“SAME”表示卷积核遍历到输入图片的每个像素，得到的特征图片与输入图片是一样大小。

tf.shape(tf.nn.conv2d(input, filter, strides=[1,1,1,1], padding=“SAME”));

卷积结果是：[1, 5, 5, 7]

5.4、用图形来表示上面的卷积过程。