被忽略的Focal Loss变种

加入极市专业CV交流群，与6000+来自腾讯，华为，百度，北大，清华，中科院等名企名校视觉开发者互动交流！更有机会与李开复老师等大牛群内互动！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。点击文末“阅读原文”立刻申请入群~

作者 | 王峰

来源 | https://zhuanlan.zhihu.com/p/62314673

已获作者授权，请勿二次转载

作者按：这篇文章其实我自己并没有完全考虑清楚，写出来希望大家一起讨论一下（见文末）。

相信大家对 Focal Loss[1] 都已经比较了解了，在网上也有大量对 Focal Loss（下面简写为FL）的解读。但是我发现很多人都没有注意到一个细节，在FL文章的附录中，提到了一种叫 FL* 的损失函数，这个损失函数的形式比FL更加简单，起到的作用与原始的FL差不多。在Kaiming He组的最新论文 TensorMask[2] 中，也是使用了这个FL的变种，而没有使用其原始形式。

TensorMask论文中使用的是FL的变种FL*

是不是不少同学都没有仔细看论文呢？原始的FL及其梯度形式实在是有点复杂：

这个梯度推导和实现起来并不容易，还好现代的框架大多都能自动求导（有些公司现场面试会要求推导这个梯度哦，有时间可以练习一下）。而FL*的形式就非常简单了：

这里因为 FL* 原始论文和TensorMask论文中最后都没有使用  项，所以我这里也将其忽略了。其实这个FL*与原始的sigmoid cross entropy loss （下称 CE loss）的区别就只在于其中的 ，它是一个超参数，实现的时候我们只要乘一下再除一下就好了，非常简单。大家都知道sigmoid函数实际上是阶跃函数的smooth版，而这个 就可以控制其smooth程度。

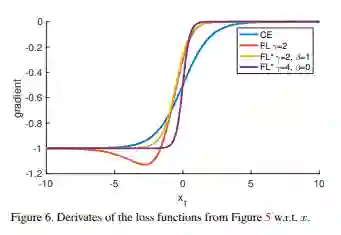
原始论文中的这张图很好地展示了  的作用：

这里的  代表的是分类的难易程度，越靠近右侧则表示这个样本被分得越好，换句话说越靠右边越简单，对于简单的样本就要给它们更接近 0 的梯度。注意看其中的蓝色曲线（即原始的CE loss），一些比较简单的样本一样能拿到不少的梯度，由于检测中（尤其是single stage detector中）存在大量的简单样本，这些简单样本拿到的梯度累积起来也是很可观的，从而冲淡了少量困难样本的梯度。

而FL*所代表的紫色曲线比蓝色曲线更加陡峭，也就是说它能更快地减小简单样本拿到的梯度，从而使网络更多地关注困难样本的分类，而不是将大量梯度都用于将简单样本分得更好。

下面我对FL*的一些疑惑了，注意看它的损失函数形式：

最后除的那个  是在损失函数外面的，由于是个超参数，所以这一项可以融入另一个超参数loss weight中。而前边的  是乘在了logit  上，这个  是神经网络的 FC 层得到的，也就是说  ，其中  是上一层的特征。那么根据神经网络的基本假设：“线性乘线性还是线性”，这个  在训练时应该会被前边的  和  吸收掉。从这个角度看， 似乎就没有意义了，一乘一除都可以被别的超参数或者网络参数给融合掉。但论文中的实验结果又很明确地表明了确实相对于原始CE有提升，对此我思考了很久都没有比较满意的结论，希望跟大家一起讨论一下。

我觉得一个可能性是weight decay的作用，  的scale是由网络的weight来决定的，如果没有weight decay，应该是可以很自由地伸缩的，乘以一个常数项并不影响其自由度。但由于weight decay的约束，整个网络的scale并不能随意扩大，所以这时再乘以一个常数，常数上并没有decay的存在，就相当于变相地降低了weight decay的效果。

这个想法只是抛砖引玉，至于其他的解读，希望大家各抒己见。

[1] Lin T Y, Goyal P, Girshick R, et al. Focal loss for dense object detection[C]//Proceedings of the IEEE international conference on computer vision. 2017: 2980-2988.

[2] Chen X, Girshick R, He K, et al. TensorMask: A Foundation for Dense Object Segmentation[J]. arXiv preprint arXiv:1903.12174, 2019.

*延伸阅读

• 一文道尽softmax loss及其变种

• 分享神经网络中设计loss function的一些技巧

点击左下角“阅读原文”，即可申请加入极市目标跟踪、目标检测、工业检测、人脸方向、视觉竞赛等技术交流群，更有每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流，一起来让思想之光照的更远吧~

觉得有用麻烦给个好看啦~